Copyright © 2021 loigiaihay.com
CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ
Bài 1. Đơn thức và đa thức nhiều biến
Bài 2. Các phép toán với đa thức nhiều biến
Bài 3. Hằng đẳng thức đáng nhớ
Bài 4. Phân tích đa thức thành nhân tử
Bài 5. Phân thức đại số
Bài 6. Cộng, trừ phân thức
Bài 7. Nhân, chia phân thức
Bài tập cuối chương 1
CHƯƠNG 2. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình chóp tam giác đều - Hình chóp tứ giác đều
Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều - hình chóp tứ giác đều
Bài tập cuối chương 2
CHƯƠNG 3. ĐỊNH LÍ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP
Bài 1. Định lí Pythagore
Bài 2. Tứ giác
Bài 3. Hình thang - Hình thang cân
Bài 4. Hình bình hành - Hình thoi
Bài 5. Hình chữ nhật - Hình vuông
Bài tập cuối chương 3
CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Thu thập và phân loại dữ liệu
Bài 2. Lựa chọn dạng biểu đồ để biểu diễn dữ liệu
Bài 3. Phân tích dữ liệu
Bài tập cuối chương 4
CHƯƠNG 5. HÀM SỐ VÀ ĐỒ THỊ
Bài 1. Khái niệm hàm số
Bài 2. Tọa độ của một điểm và đồ thị của hàm số
Bài 3. Hàm số bậc nhất y=ax+b(a≠0)
Bài 4. Hệ số góc của đường thẳng
Bài tập cuối chương 5
CHƯƠNG 6. PHƯƠNG TRÌNH
Bài 1. Phương trình bậc nhất một ẩn
Bài 2. Giải bài toán bằng cách lập phương trình bậc nhất một ẩn
Bài tập cuối chương 6
CHƯƠNG 7. ĐỊNH LÍ THALES
Bài 1. Định lí Thalès trong tam giác
Bài 2. Đường trung bình của tam giác
Bài 3. Tính chất đường phân giác của tam giác
Bài tập cuối chương 7
CHƯƠNG 8. HÌNH ĐỒNG DẠNG
Bài 1. Hai tam giác đồng dạng
Bài 2. Các trường hợp đồng dạng của hai tam giác
Bài 3. Các trường hợp đồng dạng của hai tam giác vuông
Bài 4. Hai hình đồng dạng
Bài tập cuối chương 8
CHƯƠNG 9. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Mô tả xác suất bằng tỉ số
Bài 2. Xác suất lí thuyết và xác suất thực nghiệm
Bài tập cuối chương 9
Trắc nghiệm Bài tập thực tế vận dụng định lí Thales Toán 8 có đáp án
Trắc nghiệm Bài tập thực tế vận dụng định lí Thales
13 câu hỏi
Trắc nghiệm
Câu 1 :
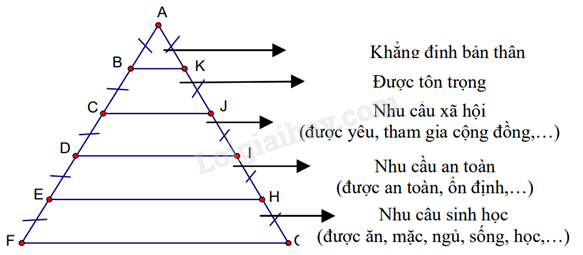
Nhà tâm lý học Abraham Maslow (1908 – 1970) được xem như một trong những người tiên phong trong trường phái Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu cầu của con người (như hình vẽ bên). Trong đó, \(BK = 6\) cm. Hãy tính đoạn thẳng \(CJ;\,EH\) ?
-
A.
\(CJ = 6{\rm{cm}};\,EH = 12{\rm{cm}}\)
-
B.
\(CJ = 12{\rm{cm}};\,EH = 24{\rm{cm}}\)
-
C.
\(CJ = 9{\rm{cm}};\,EH = 18{\rm{cm}}\)
-
D.
\(CJ = 12{\rm{cm}};\,EH = 18{\rm{cm}}\)
Câu 2 :
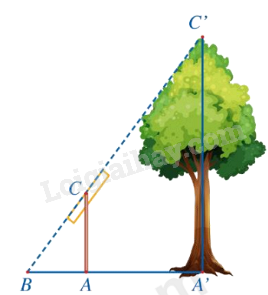
Trong hình dưới đây, độ dài đoạn thẳng \({\rm{A'C'}}\) mô tả chiều cao của một cái cây, đoạn thẳng \({\rm{AC}}\) mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm \(\left. {A',A,B} \right)\). Giả sử \(AC = 2{\rm{\;m}},AB = 1,5{\rm{\;m}},A'B = 4,5{\rm{\;m}}\). Tính chiều cao của cây.
-
A.
\(6{\rm{\;m}}\)
-
B.
\(1,5{\rm{\;m}}\)
-
C.
\(7{\rm{\;m}}\)
-
D.
\(5{\rm{\;m}}\)
Câu 3 :
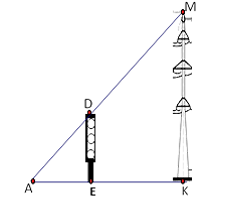
Bóng \(AK\) của một cột điện \(MK\) trên mặt đất dài \(6\,m\). Cùng lúc đó một cột đèn giao thông \(DE\) cao \(3\,m\) có bóng \(AE\) dài \(2\,m\). Chiều cao của cột điện \(MK\) là:
-
A.
\(8\,m\);
-
B.
\(9\,m\);
-
C.
\(1\,m\);
-
D.
\(4\,m\).
Câu 4 :
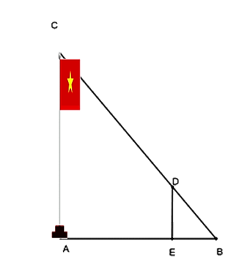
Để đo chiều cao \(AC\) của một cột cờ, người ta cắm một cái cọc \(ED\) có chiều cao \(2\,m\) vuông góc với mặt đất. Đặt vị trí quan sát tại \(B\), biết khoảng cách \(BE\) là \(1,5\,m\) và khoảng cách \(AB\) là \(9\,m\). Chiều cao \(AC\) của cột cờ là:
-
A.
\(3\,m\);
-
B.
\(6,75\,m\);
-
C.
\(12\,m\);
-
D.
\(9\,m\).
Câu 5 :
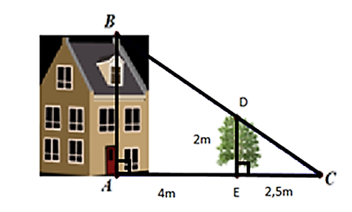
Cho hình vẽ dưới đây, biết cái cây có chiều cao \(ED = 2\,m\) và khoảng cách \(AE = 4\,m\), \(EC = 2,5\,m\). Khi đó chiều cao \(AB\) của ngôi nhà là:
-
A.
\(AB = 5,2\,m\);
-
B.
\(AB = 3,2\,m\);
-
C.
\(AB = 1,25\,m\);
-
D.
\(AB = 3,5\,m\).
Câu 6 :
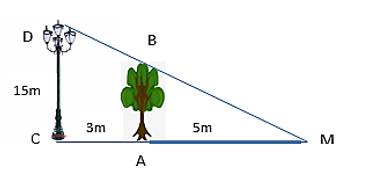
Một cột đèn cao \(15\,m\) chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn \(3\,m\) và có bóng trải dài dưới mặt đất là \(5\,m\). Tìm chiều cao của cây xanh.
-
A.
\(5,793\,m\);
-
B.
\(5,397\,m\);
-
C.
\(9,573\,m\);
-
D.
\(9,375\,m\);
Câu 7 :
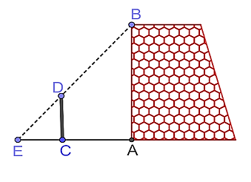
Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao \(AB\) của một bức tường như sau: Dùng một cái cọc \(CD\) đặt cố định vuông góc với mặt đất, với \(CD = 3\,m\) và \(CA = 5\,m\). Sau đó, các bạn đã phối hợp để tìm được điểm \(E\) trên mặt đất là giao điểm của hai tia \(BD,\, AC\) và đo được \(CE = 2\,m\) (Hình vẽ bên). Chiều cao \(AB\) của bức tường là:
-
A.
\(7,5\, m\);
-
B.
\(1,2\, m\);
-
C.
\(3,3\, m\);
-
D.
\(10,5\, m\).
Câu 8 :
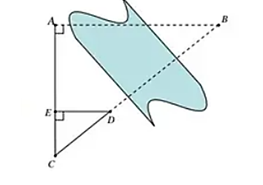
Để đo khoảng cách giữa hai điểm \(A\) và \(B\) (không thể đo trực tiếp). Người ta xác định các điểm \(C\), \(D\), \(E\) như hình vẽ. Sau đó đo được khoảng cách giữa \(A\) và \(C\) là \(AC = 4\,m\), khoảng cách giữa \(C\) và \(E\) là \(EC = 1\,m\); khoảng cách giữa \(E\) và \(D\) là \(DE = 3\,m\). Tính khoảng cách giữa hai điểm \(A\) và \(B\).
-
A.
\(21\, m\);
-
B.
\(11\, m\);
-
C.
\(12\, m\);
-
D.
\(22\, m\).
Câu 9 :
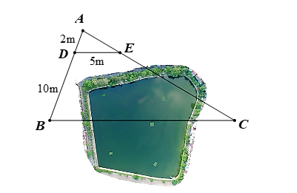
Giữa hai điểm \(B\) và \(C\) có một cái ao. Để đo khoảng cách \(BC\) người ta đo được các đoạn thẳng \(AD = 2\,m\), \(BD = 10\,m\) và \(DE = 5\,m\). Biết \(DE\parallel AB\), tính khoảng cách giữa hai điểm \(B\) và \(C\).
-
A.
\(30\, m\);
-
B.
\(25\, m\);
-
C.
\(20\, m\);
-
D.
\(15\, m\).
Câu 10 :
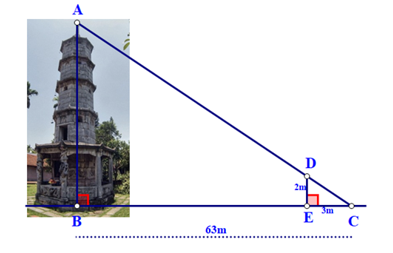
Bóng của một tháp trên mặt đất có độ dài \(BC = 63\,m\). Cùng thời điểm đó, một cây cột \(DE\) cao \(2\,m\) cắm vuông góc với mặt đất có bóng dài \(3\,m\). Chiều cao của tháp là:
-
A.
\(24\, m\);
-
B.
\(42\, m\);
-
C.
\(44\, m\);
-
D.
\(22\, m\);
Câu 11 :
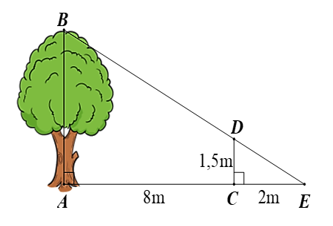
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao \(1,5\,m\) so với mặt đất, chân cọc cách gốc cây \(8\,m\) và cách bóng của đỉnh cọc \(2\,m\). Tính chiều cao của cây.
-
A.
\(7,5\, m\);
-
B.
\(6\, m\);
-
C.
\(5,5\, m\);
-
D.
\(7\, m\).
Câu 12 :
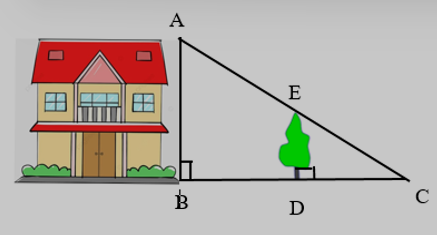
Để tính chiều cao \(AB\) của một ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây \(ED = 4\,m\) và biết được các khoảng cách \(BD = 7\,m\), \(DC = 5\,m\). Khi đó chiều cao \(AB\) của ngôi nhà là:
-
A.
\(5,6\, m\);
-
B.
\(6,9\, m\);
-
C.
\(9,6\, m\);
-
D.
\(4,36\, m\).
Câu 13 :
Một cột đèn cao \(10\;{\rm{m}}\) chiếu sáng một cây xanh (như hình vẽ). Cây cách cột đèn \(2m\) và có bóng trải dài dưới mặt đất là\(4,8\;{\rm{m}}\). Tìm chiều cao của cây xanh đó (làm tròn đến mét).
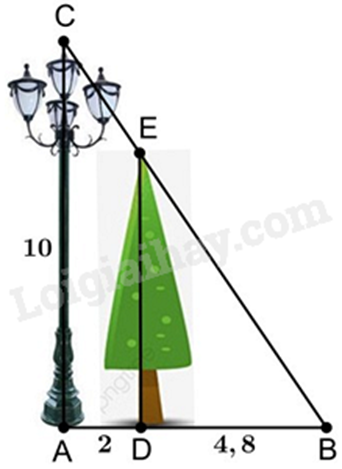
Khi đó, chiều cao của cây xanh là (làm tròn đến mét):
-
A.
\(DE \approx 14\;{\rm{m}}\).
-
B.
\(DE \approx 5m\).
-
C.
\(DE \approx 24m\).
-
D.
\(DE \approx 7m\).
