Trắc nghiệm Bài 24: Hỗn số dương Toán 6 Kết nối tri thức
Đề bài
Viết phân số \(\dfrac{4}{3}\) dưới dạng hỗn số ta được
-
A.
$1\dfrac{2}{3}$
-
B.
\(3\dfrac{1}{3}\)
-
C.
\(3\dfrac{1}{4}\)
-
D.
\(1\dfrac{1}{3}\)
Tính \(\left( { - 2\dfrac{1}{4}} \right) + \dfrac{5}{2}\)
-
A.
$ - \dfrac{1}{4}$
-
B.
\(\dfrac{3}{2}\)
-
C.
\(\dfrac{1}{4}\)
-
D.
\(\dfrac{3}{4}\)
Tìm \(x\) biết \(2\dfrac{x}{7} = \dfrac{{75}}{{35}}\)
-
A.
$x = 1$
-
B.
\(x = 2\)
-
C.
\(x = 3\)
-
D.
\(x = 4\)
Chọn câu đúng.
-
A.
\(\left( { - 3\dfrac{3}{4}} \right).1\dfrac{1}{2} = - 3\dfrac{3}{8}\)
-
B.
\(3\dfrac{3}{4}:1\dfrac{1}{5} = 3\dfrac{3}{{20}}\)
-
C.
\(\left( { - 3} \right) - \left( { - 2\dfrac{2}{5}} \right) = \dfrac{{ - 3}}{5}\)
-
D.
\(5\dfrac{7}{{10}}.15 = \dfrac{{105}}{2}\)
-
A.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{2}\)
-
B.
\(2\dfrac{1}{4}\); \(4\dfrac{1}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{2}\)
-
C.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{5}{6}\); \(9\dfrac{1}{2}\)
-
D.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{6}\)
Viết các phân số và hỗn số sau dưới dạng số thập phân:
\(\dfrac{{ - 9}}{{1\,\,000}}\)= …; \(\dfrac{{ - 5}}{8}\)= …; \(3\dfrac{2}{{25}}\)=…
-
A.
\(-0,09; -0,625; 3,08\)
-
B.
\(-0,009; -0,625; 3,08\)
-
C.
\(-0,9; -0,625; 3,08\)
-
D.
\(-0,009; -0,625; 3,008\)
Viết các số thập phân sau dưới dạng phân số tối giản:
\( - 0,125\)=…; \( - 0,012 = ...{\rm{ }}\); \( - 4,005 = ...\)
-
A.
\(\dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 4005}}{{1000}}\)
-
B.
\( \dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{25}}; \dfrac{{ - 801}}{{200}}\)
-
C.
\(\dfrac{{ - 1}}{4}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 801}}{{200}}\)
-
D.
\( \dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 801}}{{200}}\)
Tính giá trị biểu thức \(M = 60\dfrac{7}{{13}}.x + 50\dfrac{8}{{13}}.x - 11\dfrac{2}{{13}}.x\) biết \(x = - 8\dfrac{7}{{10}}\)
-
A.
$ - 870$
-
B.
\( - 87\)
-
C.
\(870\)
-
D.
\(92\dfrac{7}{{10}}\)
Tìm số tự nhiên \(x\) sao cho: \(6\dfrac{1}{3}:4\dfrac{2}{9} < x < \left( {10\dfrac{2}{9} + 2\dfrac{2}{5}} \right) - 6\dfrac{2}{9}\).
-
A.
\(x \in \left\{ {2;3;4;5;6} \right\}\)
-
B.
\(x \in \left\{ {3,4;5;6} \right\}\)
-
C.
\(x \in \left\{ {2;3,4;5} \right\}\)
-
D.
\(x \in \left\{ {3,4;5;6;7} \right\}\)
Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:
a) \(125\,d{m^2}\) b) \(218\,c{m^2}\) c) \(240\,d{m^2}\) d) \(34\,c{m^2}\)
-
A.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(\dfrac{{109}}{{5000}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{5000}}\,{m^2}\).
-
B.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(2\dfrac{9}{{50}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{5000}}\,{m^2}\).
-
C.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(2\dfrac{9}{{50}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{50}}\,{m^2}\).
-
D.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(\dfrac{{109}}{{5000}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{50}}\,{m^2}\).
Viết 2 giờ 15 phút dưới dạng hỗn số với đơn vị là giờ:
-
A.
\(1\dfrac{1}{4}\) giờ
-
B.
\(2\dfrac{1}{5}\) giờ
-
C.
\(2\dfrac{1}{4}\) giờ
-
D.
\(15\dfrac{1}{{30}}\) giờ
Lời giải và đáp án
Viết phân số \(\dfrac{4}{3}\) dưới dạng hỗn số ta được
-
A.
$1\dfrac{2}{3}$
-
B.
\(3\dfrac{1}{3}\)
-
C.
\(3\dfrac{1}{4}\)
-
D.
\(1\dfrac{1}{3}\)
Đáp án : D
+ Nếu phân số dương lớn hơn $1,$ ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu, thương tìm được là phần nguyên của hỗn số, số dư là tử của phân số kèm theo, còn mẫu vẫn là mẫu đã cho.
Ta có: \(4:3\) bằng $1$ (dư \(1\) ) nên \(\dfrac{4}{3} = 1\dfrac{1}{3}\)
Tính \(\left( { - 2\dfrac{1}{4}} \right) + \dfrac{5}{2}\)
-
A.
$ - \dfrac{1}{4}$
-
B.
\(\dfrac{3}{2}\)
-
C.
\(\dfrac{1}{4}\)
-
D.
\(\dfrac{3}{4}\)
Đáp án : C
Đổi hỗn số ra phân số rồi thực hiện phép cộng hai phân số.
\(\left( { - 2\dfrac{1}{4}} \right) + \dfrac{5}{2} = - \dfrac{9}{4} + \dfrac{5}{2}\)\( = \dfrac{{ - 9}}{4} + \dfrac{{10}}{4} = \dfrac{1}{4}\)
Tìm \(x\) biết \(2\dfrac{x}{7} = \dfrac{{75}}{{35}}\)
-
A.
$x = 1$
-
B.
\(x = 2\)
-
C.
\(x = 3\)
-
D.
\(x = 4\)
Đáp án : A
Đổi hỗn số thành phân số, đồng thời rút gọn phân số có thể rút gọn được, từ đó tìm \(x\)
\(\begin{array}{l}2\dfrac{x}{7} = \dfrac{{75}}{{35}}\\\dfrac{{2.7 + x}}{7} = \dfrac{{15}}{7}\\14 + x = 15\\x = 15 - 14\\x = 1\end{array}\)
Hỗn số \(2\dfrac{x}{7}\) các em cũng có thể coi là \(2 + \dfrac{x}{7},\) từ đó tìm \(x\) dựa vào phương pháp tìm số hạng chưa biết trong tổng.
Chọn câu đúng.
-
A.
\(\left( { - 3\dfrac{3}{4}} \right).1\dfrac{1}{2} = - 3\dfrac{3}{8}\)
-
B.
\(3\dfrac{3}{4}:1\dfrac{1}{5} = 3\dfrac{3}{{20}}\)
-
C.
\(\left( { - 3} \right) - \left( { - 2\dfrac{2}{5}} \right) = \dfrac{{ - 3}}{5}\)
-
D.
\(5\dfrac{7}{{10}}.15 = \dfrac{{105}}{2}\)
Đáp án : C
- Thực hiện các phép tính ở mỗi đáp án.
- Kết luận.
Chú ý: Đổi các hỗn số thành phân số rồi thực hiện cộng, trừ, nhân, chia các phân số.
Đáp án A: \(\left( { - 3\dfrac{3}{4}} \right).1\dfrac{1}{2}\)\( = - \dfrac{{15}}{4}.\dfrac{3}{2} = - \dfrac{{45}}{8} = - 5\dfrac{5}{8} \ne - 3\dfrac{3}{8}\)
Nên A sai.
Đáp án B: \(3\dfrac{3}{4}:1\dfrac{1}{5} = \dfrac{{15}}{4}:\dfrac{6}{5} = \dfrac{{15}}{4}.\dfrac{5}{6}\)\( = \dfrac{{25}}{8} = 3\dfrac{1}{8} \ne 3\dfrac{3}{{20}}\) nên B sai.
Đáp án C: \(\left( { - 3} \right) - \left( { - 2\dfrac{2}{5}} \right)\)\( = \left( { - 3} \right) - \left( { - \dfrac{{12}}{5}} \right) = \left( { - 3} \right) + \dfrac{{12}}{5} = \dfrac{{ - 3}}{5}\)
Nên C đúng.
Đáp án D: \(5\dfrac{7}{{10}}.15 = \dfrac{{57}}{{10}}.15 = \dfrac{{171}}{2} \ne \dfrac{{105}}{2}\) nên D sai.
-
A.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{2}\)
-
B.
\(2\dfrac{1}{4}\); \(4\dfrac{1}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{2}\)
-
C.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{5}{6}\); \(9\dfrac{1}{2}\)
-
D.
\(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{6}\)
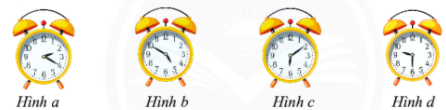
Đáp án : A
Hỗn số gồm:
Phần nguyên = số giờ
Phần phân số = Số phút: 60
Hình a: \(2\dfrac{1}{3}\)
Hình b: \(4\dfrac{5}{6}\)
Hình c: \(6\dfrac{1}{6}\)
Hình d: \(9\dfrac{1}{2}\)
Vậy ta được các hỗn số: \(2\dfrac{1}{3}\); \(4\dfrac{5}{6}\); \(6\dfrac{1}{6}\); \(9\dfrac{1}{2}\).
Viết các phân số và hỗn số sau dưới dạng số thập phân:
\(\dfrac{{ - 9}}{{1\,\,000}}\)= …; \(\dfrac{{ - 5}}{8}\)= …; \(3\dfrac{2}{{25}}\)=…
-
A.
\(-0,09; -0,625; 3,08\)
-
B.
\(-0,009; -0,625; 3,08\)
-
C.
\(-0,9; -0,625; 3,08\)
-
D.
\(-0,009; -0,625; 3,008\)
Đáp án : B
Viết các phân số và hỗn số dưới dạng các phân số có mẫu là số tròn chục, tròn trăm, tròn nghìn,…rồi viết chúng dưới dạng số thập phân.
\(\dfrac{{ - 9}}{{1\,\,000}} = - 0,009\)
\(\dfrac{{ - 5}}{8} = \dfrac{{ - 5.125}}{{8.125}} = \dfrac{{ - 625}}{{1000}} = - 0,625\)
\(3\dfrac{2}{{25}} = 3\dfrac{8}{{100}} = 3,08\)
Viết các số thập phân sau dưới dạng phân số tối giản:
\( - 0,125\)=…; \( - 0,012 = ...{\rm{ }}\); \( - 4,005 = ...\)
-
A.
\(\dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 4005}}{{1000}}\)
-
B.
\( \dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{25}}; \dfrac{{ - 801}}{{200}}\)
-
C.
\(\dfrac{{ - 1}}{4}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 801}}{{200}}\)
-
D.
\( \dfrac{{ - 1}}{8}; \dfrac{{ - 3}}{{250}}; \dfrac{{ - 801}}{{200}}\)
Đáp án : D
\(\overline {a,bcd} = \dfrac{{abcd}}{{1000}}\)
\( - 0,125 = \dfrac{{ - 125}}{{1000}} = \dfrac{{ - 125:125}}{{1000:125}} = \dfrac{{ - 1}}{8}\)
\( - 0,012 = \dfrac{{ - 12}}{{1000}} = \dfrac{{ - 12:4}}{{1000:4}} = \dfrac{{ - 3}}{{250}}\)
\( - 4,005 = \dfrac{{ - 4005}}{{1000}} = \dfrac{{ - 4005:5}}{{1000:5}} = \dfrac{{ - 801}}{{200}}\)
Tính giá trị biểu thức \(M = 60\dfrac{7}{{13}}.x + 50\dfrac{8}{{13}}.x - 11\dfrac{2}{{13}}.x\) biết \(x = - 8\dfrac{7}{{10}}\)
-
A.
$ - 870$
-
B.
\( - 87\)
-
C.
\(870\)
-
D.
\(92\dfrac{7}{{10}}\)
Đáp án : A
Thu gọn \(M\) rồi thay \(x = - 8\dfrac{7}{{10}}\) vào tính giá trị của \(M\)
\(M = 60\dfrac{7}{{13}}.x + 50\dfrac{8}{{13}}.x - 11\dfrac{2}{{13}}.x\)
\(M = \left( {60\dfrac{7}{{13}} + 50\dfrac{8}{{13}} - 11\dfrac{2}{{13}}} \right).x\)
\(M = \left[ {\left( {60 + 50 - 11} \right) + \left( {\dfrac{7}{{13}} + \dfrac{8}{{13}} - \dfrac{2}{{13}}} \right)} \right].x\)
\(M = \left( {99 + 1} \right).x = 100x\)
Thay \(x = - 8\dfrac{7}{{10}}\) vào \(M\) ta được:
\(M = 100.\left( { - 8\dfrac{7}{{10}}} \right)\) \( = 100.\left( { - \dfrac{{87}}{{10}}} \right) = - 870\)
Tìm số tự nhiên \(x\) sao cho: \(6\dfrac{1}{3}:4\dfrac{2}{9} < x < \left( {10\dfrac{2}{9} + 2\dfrac{2}{5}} \right) - 6\dfrac{2}{9}\).
-
A.
\(x \in \left\{ {2;3;4;5;6} \right\}\)
-
B.
\(x \in \left\{ {3,4;5;6} \right\}\)
-
C.
\(x \in \left\{ {2;3,4;5} \right\}\)
-
D.
\(x \in \left\{ {3,4;5;6;7} \right\}\)
Đáp án : A
Rút gọn vế trái và vế phải bằng cách đưa hỗn số về phân số. Từ đó chọn số phù hợp.
\(\begin{array}{l}6\dfrac{1}{3}:4\dfrac{2}{9} < x < \left( {10\dfrac{2}{9} + 2\dfrac{2}{5}} \right) - 6\dfrac{2}{9}\\\dfrac{{19}}{3}:\dfrac{{38}}{9} < x < \dfrac{{92}}{9} + \dfrac{{12}}{5} - \dfrac{{56}}{9}\\\dfrac{3}{2} < x < \dfrac{{32}}{5}\end{array}\)
Ta có:
\(\begin{array}{l}\dfrac{3}{2} < x < \dfrac{{32}}{5}\\1,5 < x < 6,4\end{array}\)
Vì x là số tự nhiên nên \(x \in \left\{ {2;3;4;5;6} \right\}\).
Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:
a) \(125\,d{m^2}\) b) \(218\,c{m^2}\) c) \(240\,d{m^2}\) d) \(34\,c{m^2}\)
-
A.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(\dfrac{{109}}{{5000}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{5000}}\,{m^2}\).
-
B.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(2\dfrac{9}{{50}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{5000}}\,{m^2}\).
-
C.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(2\dfrac{9}{{50}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{50}}\,{m^2}\).
-
D.
\(1\dfrac{{25}}{{100}}\,{m^2}\); \(\dfrac{{109}}{{5000}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{50}}\,{m^2}\).
Đáp án : A
Đổi các khối lượng ra các phân số có cùng đơn vị đo khối lượng
a) \(125\,d{m^2} = \dfrac{{125}}{{100}}{m^2} = 1\dfrac{{25}}{{100}}\,{m^2}\)
b) \(218\,c{m^2} = \dfrac{{218}}{{10000}}{m^2} = \dfrac{{109}}{{5000}}\,{m^2}\)
c) \(240\,d{m^2} = \dfrac{{240}}{{100}}{m^2} = 2\dfrac{{40}}{{100}}\,{m^2}\)
d) \(34\,c{m^2} = \dfrac{{34}}{{10000}}{m^2} = \dfrac{{17}}{{5000}}\,{m^2}\)
Vậy ta được: \(1\dfrac{{25}}{{100}}\,{m^2}\); \(\dfrac{{109}}{{5000}}\,{m^2}\); \(2\dfrac{{40}}{{100}}\,{m^2}\); \(\dfrac{{17}}{{5000}}\,{m^2}\).
Viết 2 giờ 15 phút dưới dạng hỗn số với đơn vị là giờ:
-
A.
\(1\dfrac{1}{4}\) giờ
-
B.
\(2\dfrac{1}{5}\) giờ
-
C.
\(2\dfrac{1}{4}\) giờ
-
D.
\(15\dfrac{1}{{30}}\) giờ
Đáp án : C
a giờ b phút = \(a + \dfrac{b}{{60}}\) (giờ)
2 giờ 15 phút = \(2 + \dfrac{{15}}{{60}} = 2 + \dfrac{1}{4} = 2\dfrac{1}{4}\) giờ.
Luyện tập và củng cố kiến thức Các dạng toán về hỗn số dương Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 25: Phép cộng và phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng và phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 26: Phép nhân và phép chia phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép nhân và phép chia phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 27: Hai bài toán về phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương VI Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về so sánh phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 24: So sánh phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về mở rộng khái niệm phân số. Phân số bằng nhau Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 23: Mở rộng phân số. Phân số bằng nhau Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập cuối chương IX Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 43: Xác suất thực nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 42: Kết quả có thể và sự kiện trong trò chơi, thí nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 41: Biểu đồ cột kép Toán 6 Kết nối tri thức với cuộc sống
- Trắc nghiệm Bài 40: Biểu đồ cột Toán 6 Kết nối tri thức










Danh sách bình luận