-
Chương 1: Tập hợp các số tự nhiên
- Bài 1: Tập hợp
- Các dạng toán về tập hợp
- Bài 2: Cách ghi số tự nhiên. Thứ tự trong tập hợp các số tự nhiên
- Các dạng toán về cách ghi số tự nhiên, thứ tự trong tập hợp các số tự nhiên
- Bài 3: Phép cộng và phép trừ số tự nhiên
- Các dạng toán về phép cộng và phép trừ số tự nhiên
- Bài 4: Phép nhân và phép chia số tự nhiên
- Các dạng toán về phép nhân và phép chia số tự nhiên
- Các dạng toán về phép nhân và phép chia số tự nhiên (tiếp)
- Bài 5: Lũy thừa với số mũ tự nhiên
- Các dạng toán về lũy thừa với số mũ tự nhiên
- Bài 6: Thứ tự thực hiện các phép tính
- Các dạng toán về thứ tự thực hiện các phép tính
- Bài tập cuối chương I
-
Chương 2: Tính chia hết trong tập hợp các số tự nhiên
- Bài 7: Quan hệ chia hết và tính chất
- Các dạng toán về quan hệ chia hết và tính chất
- Bài 8: Dấu hiệu chia hết cho 2, cho 5
- Các dạng toán về dấu hiệu chia hết cho 2, cho 5
- Bài 9: Dấu hiệu chia hết cho 3, cho 9
- Các dạng toán về dấu hiệu chia hết cho 3, cho 9
- Bài 10: Số nguyên tố
- Các dạng toán về số nguyên tố
- Bài 11: Ước chung. Ước chung lớn nhất
- Các dạng toán về ước chung, ước chung lớn nhất
- Bài 12: Bội chung. Bội chung nhỏ nhất
- Các dạng toán về bội chung, bội chung nhỏ nhất
- Bài tập cuối chương II
-
Chương 3: Số nguyên
- Bài 13: Tập hợp các số nguyên
- Các dạng toán về tập hợp các số nguyên
- Bài 14: Thứ tự trong tập hợp số nguyên
- Các dạng toán về thứ tự trong tập hợp số nguyên
- Bài 15: Phép cộng hai số nguyên
- Bài 16: Phép trừ số nguyên. Quy tắc dấu ngoặc
- Các dạng toán về phép cộng trừ số nguyên, quy tắc dấu ngoặc
- Các dạng toán về phép cộng trừ số nguyên, quy tắc dấu ngoặc (tiếp)
- Bài 17: Phép nhân số nguyên, phép chia hết, bội và ước của một số nguyên
- Các dạng toán phép nhân, chia số nguyên, bội và ước của một số nguyên
- Các dạng toán về phép nhân, chia số nguyên, bội và ước của một số nguyên (tiếp)
- Bài tập cuối chương III
-
Chương 4: Một số hình phẳng trong thực tiễn
-
Chương 5: Tính đối xứng của hình phẳng trong thực tiễn
-
Chương 6: Phân số
- Bài 23: Mở rộng phân số. Phân số bằng nhau
- Các dạng toán về mở rộng khái niệm phân số. Phân số bằng nhau
- Tính chất cơ bản của phân số
- Các dạng toán về tính chất cơ bản của phân số
- Bài 24: So sánh phân số
- Các dạng toán về so sánh phân số
- Bài 24: Hỗn số dương
- Các dạng toán về hỗn số dương
- Bài 25: Phép cộng và phép trừ phân số
- Các dạng toán về phép cộng và phép trừ phân số
- Bài 26: Phép nhân và phép chia phân số
- Các dạng toán về phép nhân và phép chia phân số
- Bài 27: Hai bài toán về phân số
- Bài tập cuối chương VI
-
Chương 7: Số thập phân
-
Chương 8: Những hình hình học cơ bản
-
Chương 9: Dữ liệu và xác suất thực nghiệm
Trắc nghiệm Các dạng toán về tập hợp Toán 6 Kết nối tri thức
Đề bài
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Viết tập hợp \(P\) các chữ cái khác nhau trong cụm từ: “ HOC SINH”
-
A.
\(P = \left\{ {H;O;C;S;I;N;H} \right\}.\)
-
B.
\(P = \left\{ {H;O;C;S;I;N} \right\}.\)
-
C.
\(P = \left\{ {H;C;S;I;N} \right\}.\)
-
D.
\(P = \left\{ {H;O;C;H;I;N} \right\}.\)
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Cho hình vẽ.
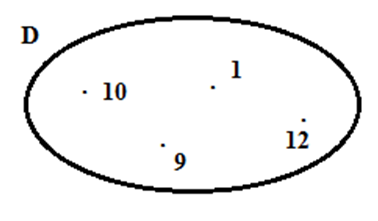
Tập hợp \(D\) là
-
A.
\(D = \left\{ {8;9;10;12} \right\}\)
-
B.
\(D = \left\{ {1;9;10} \right\}\)
-
C.
\(D = \left\{ {9;10;12} \right\}\)
-
D.
\(D = \left\{ {1;9;10;12} \right\}\)
Cho B là tập hợp các số tự nhiên nhỏ hơn 10. Trong các khẳng định sau, có bao nhiêu khẳng định sai?
1. \(2 \in B\)
2. \(5 \notin B\)
3. \(B = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
4. \(B = \left\{ {9;8;7;6;5;4;3;2;1;0} \right\}\)
5. \(B = \left\{ {0;1;1;2;3;4;5;6;7;8;9} \right\}\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Tập hợp \(P\) gồm các số tự nhiên lớn hơn \(50\) và không lớn hơn \(57\). Kết luận nào sau đây là sai?
-
A.
\(55 \in P\)
-
B.
\(57 \in P\)
-
C.
\(50 \notin P\)
-
D.
\(58 \in P\)
Cho hình vẽ sau:
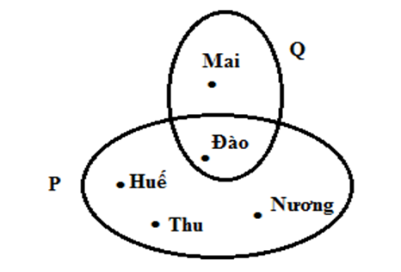
Viết tập hợp P và Q.
-
A.
P={Huế; Thu; Nương}; Q={Đào; Mai}
-
B.
P={Huế; Thu; Nương; Đào}; Q={Đào; Mai}
-
C.
P={Huế; Thu; Nương; Đào}; Q={Mai}
-
D.
P={Huế; Thu; Đào}; Q={Đào; Mai}
Cho hình vẽ sau:
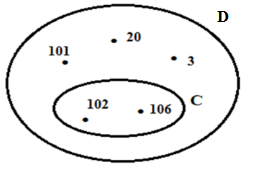
Viết tập hợp C và D.
-
A.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {20;101;102;106} \right\}\)
-
B.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;102;106} \right\}\)
-
C.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101} \right\}\)
-
D.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Cho tập hợp \(A = \left\{ {x \in N|2 < x \le 7} \right\}\) . Kết luận nào sau đây không đúng?
-
A.
\(7 \in A\)
-
B.
Tập hợp $A$ có $5$ phần tử
-
C.
\(2 \in A\)
-
D.
Tập hợp $A$ gồm các số tự nhiên lớn hơn $2$ và nhỏ hơn hoặc bằng $7$
Tập hợp \(C\) các số tự nhiên \(x\) sao cho \(x - 10 = 15\) có số phần tử là
-
A.
\(4\)
-
B.
\(2\)
-
C.
\(1\)
-
D.
\(3\)
Cho tập hợp \(A = \left\{ {x \in N|1990 \le x \le 2009} \right\}\). Số phần tử của tập hợp \(A\) là
-
A.
\(20\)
-
B.
\(21\)
-
C.
\(19\)
-
D.
\(22\)
Lời giải và đáp án
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Đáp án : A
Viết tập hợp \(A\) dưới dạng liệt kê các phần tử thỏa mãn đề bài.
Tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10\) là \(A = \left\{ {6;7;8;9} \right\}.\)
Viết tập hợp \(P\) các chữ cái khác nhau trong cụm từ: “ HOC SINH”
-
A.
\(P = \left\{ {H;O;C;S;I;N;H} \right\}.\)
-
B.
\(P = \left\{ {H;O;C;S;I;N} \right\}.\)
-
C.
\(P = \left\{ {H;C;S;I;N} \right\}.\)
-
D.
\(P = \left\{ {H;O;C;H;I;N} \right\}.\)
Đáp án : B
Viết tập hợp \(P\) dưới dạng liệt kê các phần tử thỏa mãn đề bài.
Các chữ cái khác nhau trong cụm từ “ HOC SINH” là H;O;C;S;I;N
Nên \(P = \left\{ {H;O;C;S;I;N} \right\}.\)
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Đáp án : B
+ Tìm tính chất chung của các phần tử trong tập hợp
+ Viết tập hợp dưới dạng chỉ ra tính chất đặc trưng
Nhận thấy các số \(16;17;18;19\) là các số tự nhiên lớn hơn \(15\) và nhỏ hơn \(20\)
Nên \(A = \left\{ {x \in N |15 < x < 20} \right\}\).
Cho hình vẽ.
Tập hợp \(D\) là
-
A.
\(D = \left\{ {8;9;10;12} \right\}\)
-
B.
\(D = \left\{ {1;9;10} \right\}\)
-
C.
\(D = \left\{ {9;10;12} \right\}\)
-
D.
\(D = \left\{ {1;9;10;12} \right\}\)
Đáp án : D
+ Các phần tử nằm trong vòng tròn là các phần tử thuộc tập hợp D.
Ta có các số trong vòng tròn là \(1,9,10,12\) nên tập hợp \(D = \left\{ {1;9;10;12} \right\}\).
Cho B là tập hợp các số tự nhiên nhỏ hơn 10. Trong các khẳng định sau, có bao nhiêu khẳng định sai?
1. \(2 \in B\)
2. \(5 \notin B\)
3. \(B = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
4. \(B = \left\{ {9;8;7;6;5;4;3;2;1;0} \right\}\)
5. \(B = \left\{ {0;1;1;2;3;4;5;6;7;8;9} \right\}\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
+) Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,” hoặc dấu “;”(đối với trường hợp là các phần tử số).
+) Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
+) Phần tử \(x\) thuộc tập hợp \(A\) được kí hiệu là \(x \in A\), đọc là “x thuộc A”. Phần tử \(y\) không thuộc tập hợp \(A\) được kí hiệu là \(y \notin A\), đọc là “y không thuộc A”.
Số 2 là số tự nhiên nhỏ hơn 10 nên \(2 \in B\) =>Khẳng định 1 đúng.
Số 5 là số tự nhiên nhỏ hơn 10 nên \(5 \in B\) =>Khẳng định 2 sai.
Tập hợp B là tập hợp các số tự nhiên nhỏ hơn 10 nên các phần tử của B là:
1;2;3;4;5;6;7;8;9
\( \Rightarrow B = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\)\( = \left\{ {9;8;7;6;5;4;3;2;1} \right\}\) =>Khẳng định 4 đúng.
Tập hợp B trong khẳng định 3 có chứa số 10 mà 10 không thuộc B =>Khẳng định 3 sai.
\(B = \left\{ {1;1;2;3;4;5;6;7;8;9} \right\}\) có số 1 được liệt kê hai lần => Khẳng định 5 sai
Vậy có 3 khẳng định sai.
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Đáp án : C
+ Chỉ ra các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27.\)
+ Từ đó viết tập hợp A dưới dạng liệt kê.
Các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27\) là \(23;24;25;26;27.\)
Nên \(A = \left\{ {23;24;25;26;27} \right\}.\)
Tập hợp \(P\) gồm các số tự nhiên lớn hơn \(50\) và không lớn hơn \(57\). Kết luận nào sau đây là sai?
-
A.
\(55 \in P\)
-
B.
\(57 \in P\)
-
C.
\(50 \notin P\)
-
D.
\(58 \in P\)
Đáp án : D
+ Viết tập hợp \(P\) dưới dạng liệt kê.
+ Chỉ ra các phần tử thuộc \(P\) và không thuộc \(P\) để chọn đáp án.
Các số tự nhiên lớn hơn \(50\) và không lớn hơn \(57\) là \(51;52;53;54;55;56;57\)
Nên \(P = \left\{ {51;52;53;54;55;56;57} \right\}\)
Do đó \(58 \notin P\) nên D sai.
Cho hình vẽ sau:
Viết tập hợp P và Q.
-
A.
P={Huế; Thu; Nương}; Q={Đào; Mai}
-
B.
P={Huế; Thu; Nương; Đào}; Q={Đào; Mai}
-
C.
P={Huế; Thu; Nương; Đào}; Q={Mai}
-
D.
P={Huế; Thu; Đào}; Q={Đào; Mai}
Đáp án : B
Các phần tử trong vòng tròn là các phần tử của tập hợp. Nhìn vào hình vẽ để viết các tập hợp.
Ta có P={Huế; Thu; Nương; Đào}
Q={Đào; Mai}
Cho hình vẽ sau:
Viết tập hợp C và D.
-
A.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {20;101;102;106} \right\}\)
-
B.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;102;106} \right\}\)
-
C.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101} \right\}\)
-
D.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Đáp án : D
Các phần tử trong vòng tròn là các phần tử thuộc tập hợp.
Từ hình vẽ ta viết các tập hợp dưới dạng liệt kê.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Cho tập hợp \(A = \left\{ {x \in N|2 < x \le 7} \right\}\) . Kết luận nào sau đây không đúng?
-
A.
\(7 \in A\)
-
B.
Tập hợp $A$ có $5$ phần tử
-
C.
\(2 \in A\)
-
D.
Tập hợp $A$ gồm các số tự nhiên lớn hơn $2$ và nhỏ hơn hoặc bằng $7$
Đáp án : C
Sử dụng tính chất đặc trưng của phần tử trong tập hợp để tìm đáp án.
Trong cách viết \(A = \left\{ {x \in N|2 < x \le 7} \right\}\), ta chỉ ra tính chất đặc trưng cho các phần tử \(x\) của tập hợp A đó là \(x > 2\) và \(x \le 7\) .
Khi đó tập hợp A gồm các phần tử 3, 4, 5, 6, 7
Do đó \(2\) không là phần tử của tập \(A\).
Tập hợp \(C\) các số tự nhiên \(x\) sao cho \(x - 10 = 15\) có số phần tử là
-
A.
\(4\)
-
B.
\(2\)
-
C.
\(1\)
-
D.
\(3\)
Đáp án : C
Tìm các giá trị của \(x\) thỏa mãn \(x - 10 = 15\)
Sau đó suy ra số phần tử của tập hợp \(C.\)
Ta có \(x - 10 = 15\)
\(x = 15+10\)
$x=25$
nên \(C = \left\{ {25} \right\}\) do đó \(C\) có một phần tử.
Cho tập hợp \(A = \left\{ {x \in N|1990 \le x \le 2009} \right\}\). Số phần tử của tập hợp \(A\) là
-
A.
\(20\)
-
B.
\(21\)
-
C.
\(19\)
-
D.
\(22\)
Đáp án : A
Đếm các số tự nhiên từ \(1990\) đến \(2000.\)
Tập hợp các số tự nhiên liên tiếp từ \(a\) đến \(b\) có \(b - a + 1\) phần tử.
Các số tự nhiên liên tiếp hơn kém nhau \(1\) đơn vị. Vì vậy số phần tử của tập hợp \(A\) là:
\(2009 - 1990 + 1 = 20.\)
Luyện tập và củng cố kiến thức Bài 2: Cách ghi số tự nhiên. Thứ tự trong tập hợp các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về cách ghi số tự nhiên, thứ tự trong tập hợp các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Phép cộng và phép trừ số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng và phép trừ số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Phép nhân và phép chia số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép nhân và phép chia số tự nhiên Toán 6 Kết nối tri thức với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép nhân và phép chia số tự nhiên (tiếp) Toán 6 Kết nối tri thức với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Lũy thừa với số mũ tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về lũy thừa với số mũ tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương I Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Tập hợp Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập cuối chương IX Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 43: Xác suất thực nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 42: Kết quả có thể và sự kiện trong trò chơi, thí nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 41: Biểu đồ cột kép Toán 6 Kết nối tri thức với cuộc sống
- Trắc nghiệm Bài 40: Biểu đồ cột Toán 6 Kết nối tri thức
