Trắc nghiệm Các dạng toán về tập hợp các số nguyên Toán 6 Kết nối tri thức
Đề bài
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
-
A.
$3$
-
B.
$ - 3$
-
C.
$ - 4$
-
D.
$4$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
-
A.
$3$
-
B.
$5$
-
C.
$2$
-
D.
$4$
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
-
A.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
-
B.
\(D = \left\{ { - 3; - 2} \right\}.\)
-
C.
\(D = \left\{ {0;1;6;10} \right\}.\)
-
D.
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
-
A.
$3$ và \( - 3\)
-
B.
$2$ và \( - 2\)
-
C.
$2$ và \( - 3\)
-
D.
$3$ và \( - 2\)
Những điểm cách điểm 3 năm đơn vị là:
-
A.
$7$ và \( - 1\)
-
B.
$6$ và \( - 2\)
-
C.
$2$ và \( - 2\)
-
D.
$8$ và \( - 2\)
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
-
A.
$3$
-
B.
$5$
-
C.
$6$
-
D.
$7$
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
-
A.
$3$
-
B.
$5$
-
C.
$2$
-
D.
$4$
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
-
A.
$6$
-
B.
$ - 8$
-
C.
$4$
-
D.
$5$
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
-
A.
\(120\,\,(m)\)
-
B.
\( - 120\,\,(m)\)
-
C.
\( + \,120\,(m)\)
-
D.
\(120\, - \,(m)\)
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
-
A.
\(5\,000\,000\) đồng
-
B.
\(5\,\,000\,\,000\,\, - \) đồng
-
C.
\( - \,5\,\,000\,\,000\) đồng
-
D.
\( + \,5\,000\,\,000\) đồng
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
-
A.
\(776\)
-
B.
\( - 776\)
-
C.
\( + 776\)
-
D.
\( - 767\)
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(4\)
Cách viết nào sau đây là đúng:
-
A.
\( - 2 \in \mathbb{N}\)
-
B.
\(1,5 \in \mathbb{Z}\)
-
C.
\( - 31 \in \mathbb{Z}\)
-
D.
\(1\dfrac{1}{2} \in \mathbb{Z}\)
-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
-
A.
\(4\)
-
B.
\( - 7\)
-
C.
\(7\)
-
D.
\(6\)
-
A.
\({8^o}C\)
-
B.
\( - {3^o}C\)
-
C.
\({3^o}C\)
-
D.
\({6^o}C\)
Lời giải và đáp án
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
-
A.
$3$
-
B.
$ - 3$
-
C.
$ - 4$
-
D.
$4$
Đáp án : C
- Sử dụng trục số để tìm đáp án
+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
Điểm cách $ - 1$ ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị.
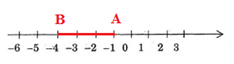
Điểm nằm bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị là điểm $ - 4$
Nên điểm cách $ - 1$ ba đơn vị theo chiều âm là $ - 4.$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
-
A.
$3$
-
B.
$5$
-
C.
$2$
-
D.
$4$
Đáp án : D
- Sử dụng kiến thức về trục số để xác định khoảng cách từ điểm \(6\) đến điểm \(2\).
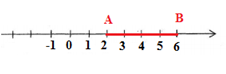
Điểm \(6\) cách điểm \(2\) là bốn đơn vị
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
-
A.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
-
B.
\(D = \left\{ { - 3; - 2} \right\}.\)
-
C.
\(D = \left\{ {0;1;6;10} \right\}.\)
-
D.
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Đáp án : B
- Chọn ra các số nguyên âm trong các phần tử thuộc tập hợp \(C.\)
- Viết tập hợp \(D\) gồm các phần tử là các số vừa tìm được.
Ta có \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\) có các số nguyên âm là \( - 3; - 2\). Nên tập hợp \(D = \left\{ { - 3; - 2} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
-
A.
$3$ và \( - 3\)
-
B.
$2$ và \( - 2\)
-
C.
$2$ và \( - 3\)
-
D.
$3$ và \( - 2\)
Đáp án : A
Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị, điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị.
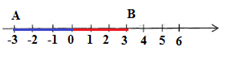
Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$
Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.
Những điểm cách điểm 3 năm đơn vị là:
-
A.
$7$ và \( - 1\)
-
B.
$6$ và \( - 2\)
-
C.
$2$ và \( - 2\)
-
D.
$8$ và \( - 2\)
Đáp án : D
Những điểm cách điểm $3$ năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.
Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$
Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
-
A.
$3$
-
B.
$5$
-
C.
$6$
-
D.
$7$
Đáp án : C
Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)
Vậy có \(6\) số thỏa mãn điều kiện đề bài.
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
-
A.
$3$
-
B.
$5$
-
C.
$2$
-
D.
$4$
Đáp án : B
Dựa vào trục số để xác định.
Lưu ý: Gốc trên trục tọa độ là điểm $0.$
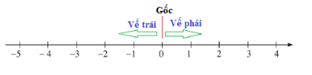
Quan sát trục số ta thấy:
Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$
Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$
Điểm $ - 4$ cách điểm $1$ là năm đơn vị.
Vậy điểm A cách điểm B là $5$ đơn vị.
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
-
A.
$6$
-
B.
$ - 8$
-
C.
$4$
-
D.
$5$
Đáp án : C
Điểm nằm cách điểm A theo chiều dương tức là điểm đó nằm bên tay phải điểm A
Điểm nằm cách điểm A theo chiều âm tức là điểm đó nằm bên trái điểm A

Ta đếm về bên phải số $ - 2$ sáu đơn vị được số $4$ ( hay $ + 4$ )
Vậy số cách số $ - 2$ sáu đơn vị theo chiều dương là: $4$ ( hay $ + 4$)
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
-
A.
\(120\,\,(m)\)
-
B.
\( - 120\,\,(m)\)
-
C.
\( + \,120\,(m)\)
-
D.
\(120\, - \,(m)\)
Đáp án : B
Số nguyên âm biểu thị vị trí dưới mực nước biển \(a\,\,\left( m \right)\) là: \( - a\,\,\left( m \right)\).
Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là: \( - 120\,\,m\).
Viết dấu “ - ” sau đó đến số và cuối cùng là đơn vị đo.
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
-
A.
\(5\,000\,000\) đồng
-
B.
\(5\,\,000\,\,000\,\, - \) đồng
-
C.
\( - \,5\,\,000\,\,000\) đồng
-
D.
\( + \,5\,000\,\,000\) đồng
Đáp án : C
Số nguyên âm biểu thị số tiền nợ (lỗ) \(a\,\,\)đồng là: \( - a\,\,\) đồng.
Do ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng nên ta có thể nói ông Hai có \( - \,5\,\,000\,\,000\) đồng.
Viết dấu “ - ” sau đó đến số tiền nợ (lỗ).
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
-
A.
\(776\)
-
B.
\( - 776\)
-
C.
\( + 776\)
-
D.
\( - 767\)
Đáp án : B
Số nguyên âm biểu thị năm \(a\) trước công nguyên là: \( - a\).
Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên tức là nó diễn ra vào năm \( - 776\)
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(4\)
Đáp án : C
Tập hợp số gồm các số nguyên âm, số \(0\) và các số nguyên dương được gọi là tập hợp số nguyên.
Các số \(- \dfrac{4}{3};\,0,5;\,1\dfrac{2}{7}\) không phải là số nguyên.
Các số là số nguyên là: \( - 2;\,\,4;\, - 100\).
Vậy có \(3\) số là số nguyên.
0,5 là số thập phân.
Cách viết nào sau đây là đúng:
-
A.
\( - 2 \in \mathbb{N}\)
-
B.
\(1,5 \in \mathbb{Z}\)
-
C.
\( - 31 \in \mathbb{Z}\)
-
D.
\(1\dfrac{1}{2} \in \mathbb{Z}\)
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => A sai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, D sai.
\( - 31\) là số nguyên => C đúng.
-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
Đáp án : B
-
A.
\(4\)
-
B.
\( - 7\)
-
C.
\(7\)
-
D.
\(6\)
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Khoảng cách giữa hai điểm luôn dương.
-
A.
\({8^o}C\)
-
B.
\( - {3^o}C\)
-
C.
\({3^o}C\)
-
D.
\({6^o}C\)
Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
Luyện tập và củng cố kiến thức Bài 14: Thứ tự trong tập hợp số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về thứ tự trong tập hợp số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 15: Phép cộng hai số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 16: Phép trừ số nguyên. Quy tắc dấu ngoặc Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng trừ số nguyên, quy tắc dấu ngoặc Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng trừ số nguyên, quy tắc dấu ngoặc (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 17: Phép nhân số nguyên, phép chia hết, bội và ước của một số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán phép nhân, chia số nguyên, bội và ước của một số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép nhân, chia số nguyên, bội và ước của một số nguyên (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương III Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 13: Tập hợp các số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập cuối chương IX Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 43: Xác suất thực nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 42: Kết quả có thể và sự kiện trong trò chơi, thí nghiệm Toán 6 Kết nối tri thức
- Trắc nghiệm Bài 41: Biểu đồ cột kép Toán 6 Kết nối tri thức với cuộc sống
- Trắc nghiệm Bài 40: Biểu đồ cột Toán 6 Kết nối tri thức










Danh sách bình luận