Bài 7 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo

Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:

a) \(\frac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\).

b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\).

Phương pháp giải - Xem chi tiết

Vẽ hình sử dụng đường tròn lượng giác.

Lời giải chi tiết

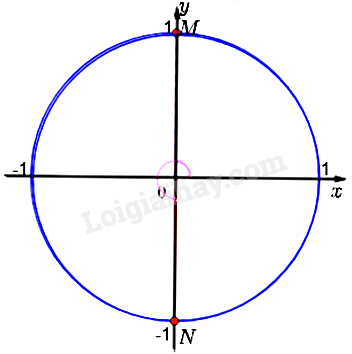
a) Thay k = 0, 1, 2,... Ta được các điểm M, N là điểm biểu diễn của góc \(\frac{\pi }{2};\frac{{3\pi }}{2};...\)

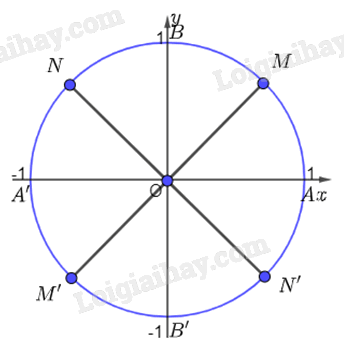
b) Thay k = 0, 1, 2, 3,... Ta được các điểm A, M, B, N, A' M', B', N là điểm biểu diễn của góc \(0;\frac{\pi }{4};\frac{\pi }{2};\frac{{3\pi }}{4};\pi ;\frac{{5\pi }}{4};\frac{{3\pi }}{2};\frac{{7\pi }}{4};2\pi ;...\)

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 15 phiếu

Bài tiếp theo

Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
Bài 9 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Bài 5 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14
Bài 4 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Góc lượng giác (frac{{31pi }}{7}) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
Bài 2 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Đổi số đo của các góc sau đây sang độ:
Bài 1 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Đổi số đo của các góc sau đây sang radian
Giải mục 3 trang 10, 11 SGK Toán 11 tập 1 - Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0). a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 - Chân trời sáng tạo
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9).
Giải mục 1 trang 7, 8, 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
Hoạt động 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA. a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây,
Giải câu hỏi mở đầu trang 7 SGK Toán 11 tập 1 - Chân trời sáng tạo
Mỗi hình dưới đây thể hiện chuyển động quay của một điểm trên bánh lái tàu từ vị trí A đến vị trí B. Các chuyển động này có điểm nào giống nhau, điểm nào khác nhau?
Lý thuyết Góc lượng giác - SGK Toán 11 Chân trời sáng tạo
1. Góc lượng giác