Toán 11, giải toán lớp 11 chân trời sáng tạo Bài 4. Hàm số lượng giác và đồ thị Toán 11 Chân trời sá..

Bài 7 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo


Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất.

Đã có lời giải SGK Toán lớp 12 - Chân trời sáng tạo (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, \(\alpha \) là góc lượng giác \((Tx,{\rm{ }}TA)\) \((0 < \alpha  < \pi ).\)

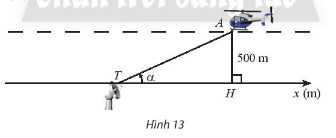
a) Biểu diễn toạ độ \({x_H}\) của điểm H trên trục \({T_x}\) theo \(\alpha \).

b) Dựa vào đồ thị hàm số côtang, hãy cho biết với \(\frac{\pi }{6} < \alpha  < \frac{{2\pi }}{3}\) thì \({x_H}\) nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.

Phương pháp giải - Xem chi tiết

Dựa vào hình vẽ và sử dụng đồ thị hàm số côtang để giải.

Lời giải chi tiết

a) Xét tam giác AHT vuông tại H có:

\(\cot \alpha  = \frac{{TH}}{{AH}} \Leftrightarrow TH = AH.\cot \alpha  = 500.\cot \alpha \)

Vậy trên trục \({T_x}\) tọa độ \({x_H} = 500.\cot \alpha \).

b) Ta có đồ thị của hàm số\(y = cot\alpha \)trong khoảng \(\frac{\pi }{6} < \alpha  < \frac{{2\pi }}{3}\) là:

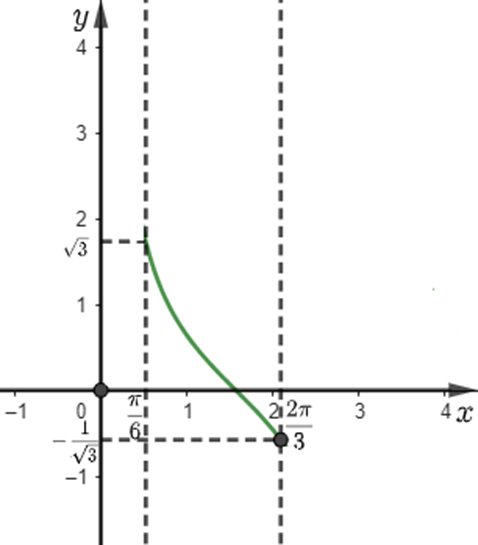
Khi đó \(-\;\frac{1}{{\sqrt 3 }} < cot\alpha  < \frac{1}{{\sqrt 3 }} \Leftrightarrow -\;\frac{{500}}{{\sqrt 3 }} < 500.cot\alpha  < \frac{{500}}{{\sqrt 3 }}\)

\( \Leftrightarrow -\;\frac{{500}}{{\sqrt 3 }} < {x_H} < \frac{{500}}{{\sqrt 3 }} \Leftrightarrow  - 288,7 < {x_H} < 866\).

Vậy \({x_H}\; \in \;\{  - 288,7;866\} \).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua