Trắc nghiệm Bài 6,7: Các phép tính với số thập phân Toán 6 Cánh diều
Đề bài
Giá trị của \(N = - \dfrac{1}{7}\left( {9\dfrac{1}{2} - 8,75} \right):\dfrac{2}{7} + 0,625:1\dfrac{2}{3}\) là
-
A.
$ - \dfrac{5}{6}$
-
B.
\(0\)
-
C.
\( - \dfrac{6}{5}\)
-
D.
\(1\)
Khoảng cách từ nhà An đến trường học là 3km, mỗi ngày An đạp xe đến trường với vận tốc 15km/h. Vậy An đi tới trường hết
phút
Thực hiện phép tính sau: \(12,3 + 5,67\) ta được kết quả là
Kết quả của phép tính \(\left( { - 12,3} \right) + \left( { - 5,67} \right)\) là
Thực hiện phép tính \( - 5,5 + 90,67\) ta được kết quả là:
Kết quả của phép trừ \(0,008 - 3,9999\) là:
Cho biết một quả chuối nặng 100 g có chứa:
- Chất béo: 0,3 g
- Kali: 0,42 g.
Trong quả chuối đó, khối lượng kali nhiều hơn khối lượng chất béo là
g
Tính một cách hợp lí: \(89,45 + \left( { - 3,28} \right) + 0,55 + \left( { - 6,72} \right)\) ta được kết quả bằng
-
A.
\(80\)
-
B.
\(-80\)
-
C.
\(100\)
-
D.
\(-100\)
Bạn Nam cao 1,57 m, bạn Linh cao 1,53 m, bạn Loan cao 1,49 m.
Trong ba bạn đó, bạn nào cao nhất? Bạn nào thấp nhất?
-
A.
Bạn Nam cao nhất, bạn Loan thấp nhất
-
B.
Bạn Linh cao nhất, bạn Loan thấp nhất
-
C.
Bạn Nam cao nhất, bạn Linh thấp nhất
-
D.
Bạn Loan cao nhất, bạn Nam thấp nhất
Chiều cao của bạn cao nhất hơn bạn thấp nhất là bao nhiêu mét?
-
A.
\(0,18\,m\)
-
B.
\(0,08\,m\)
-
C.
\(0,04\,m\)
-
D.
\(0,14\,m\)
Bác Đồng của ba thanh gỗ: thanh thứ nhất dài 1,85 m, thanh thứ hai dài hơn thanh thứ nhất 10 cm. Độ dài thanh gỗ thứ ba ngắn hơn tổng độ dài hai thanh gỗ đầu tiên là 1,35 m. Thanh gỗ thứ ba mà bác Đồng đã cưa dài bao nhiêu mét?
-
A.
\(1,95\,m\)
-
B.
\(3,8\,m\)
-
C.
\(2,45\,m\)
-
D.
\(2,38\,m\)
-
A.
\(8,75\)(cm)
-
B.
\(9,75(cm^2)\)
-
C.
\(7,55(cm^2)\)
-
D.
\(9,75\)(cm)
Thực hiện phép tính: \(\left( { - 4,5} \right) + 3,6 + 4,5 + \left( { - 3,6} \right)\) ta được kết quả là:
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\)
Thực hiện các phép tính sau: \( - 0,18.\left( { - 1,5} \right)\) ta được kết quả là:
-
A.
\( - 0,27\)
-
B.
\( - 2,7\)
-
C.
\(0,27\)
-
D.
\(2,7\)
Thực hiện các phép tính sau: \(\left( { - {\rm{ }}45,5} \right).{\rm{ }}0,4\) ta được kết quả là:
-
A.
\(18,2\)
-
B.
\( - 18,2\)
-
C.
\( - 182\)
-
D.
\( - 1,82\)
Tính diện tích S của một hình tròn có bán kính \(R = 10{\rm{ }}cm\) theo công thức \(S = \pi {R^2}\) với \(\pi = 3,14\)
-
A.
\(31,4\,\,c{m^2}\)
-
B.
\(314\,c{m^2}\)
-
C.
\(64,8\,c{m^2}\)
-
D.
\(314\,c{m^3}\)
Thực hiện các phép tính sau: \(0,15.4,4\) ta được kết quả là:
-
A.
\(6,6\)
-
B.
\(0,66\)
-
C.
\(6,60\)
-
D.
\(0,066\)
Thực hiện phép tính: \(3,176 - \left( {2,104 + 1,18} \right)\) ta được kết quả là
Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là
\(cm^2\)

Khối lượng vitamin C trung bình trong một quả ớt chuông là 0,135 g, còn trong một quả cam là 0,045 g. Khối lượng vitamin C trong quả ớt chuông gấp bao nhiêu lần trong quả cam?
-
A.
2 lần
-
B.
3 lần
-
C.
4 lần
-
D.
5 lần
Tính chu vi của một hình tròn có bán kính R = 1,25 m theo công thức C = \(2\pi R\) với \(\pi \) = 3,142.
-
A.
7,855 m
-
B.
7,855 m2
-
C.
7,585 m
-
D.
7,558 m

Tìm \(y\), biết: \(135,2 - y = 52,53 + 16,7\).
A. \(y = 65,97\)
B. \(y = 66,2\)
C. \(y = 82,67\)
D. \(y = 204,43\)

Điền số thích hợp vào ô trống để tính bằng cách thuận tiện:
\(245,18 - 81,359 - 17,641 + 113,82\)
\( = (245,18 + \)
\( ) \, - \,(81,359 + \)
\( ) \)
\( = \)
\(- \)
\( =\)
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một cửa hàng có \(58,5kg\) gạo nếp, số gạo tẻ nhiều hơn gạo nếp \(33,8kg\). Vậy cửa hàng có tất cả
tạ gạo.

\(24,225km + 818m - 67,9hm = ...km\).
Số thích hợp điền vào chỗ chấm là:
A. \(18,253\)
B. \(25,615\)
C. \(31,726\)
D. \(774,325\)
Điền số thích hợp vào ô trống:
Cho đường gấp khúc ABCD như hình vẽ:
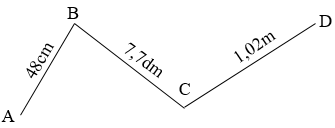
Độ dài đường gấp khúc đó là
\( m.\)

$385,18$ trừ đi hiệu của $207,4$ và $91,28$ rồi cộng với $115$ được kết quả là:
A. \(201,5\)
B. \(231,12\)
C. \(384,06\)
D. \(616,33\)
Lời giải và đáp án
Giá trị của \(N = - \dfrac{1}{7}\left( {9\dfrac{1}{2} - 8,75} \right):\dfrac{2}{7} + 0,625:1\dfrac{2}{3}\) là
-
A.
$ - \dfrac{5}{6}$
-
B.
\(0\)
-
C.
\( - \dfrac{6}{5}\)
-
D.
\(1\)
Đáp án : B
Đổi các hỗn số, số thập phân thành phân số rồi thực hiện phép tính.
Lưu ý thứ tự thực hiện phép tính nếu có ngoặc thì thực hiện trong ngoặc trước.
\(N = - \dfrac{1}{7}\left( {9\dfrac{1}{2} - 8,75} \right):\dfrac{2}{7} + 0,625:1\dfrac{2}{3}\)
\(N = - \dfrac{1}{7}\left( {\dfrac{{19}}{2} - \dfrac{{875}}{{100}}} \right).\dfrac{7}{2} + \dfrac{{625}}{{1000}}:\dfrac{5}{3}\)
\(N = - \dfrac{1}{7}\left( {\dfrac{{19}}{2} - \dfrac{{35}}{4}} \right).\dfrac{7}{2} + \dfrac{5}{8}.\dfrac{3}{5}\)
\(N = - \dfrac{1}{7}.\dfrac{3}{4}.\dfrac{7}{2} + \dfrac{3}{8}\)
\(N = - \dfrac{3}{8} + \dfrac{3}{8} = 0\)
Khoảng cách từ nhà An đến trường học là 3km, mỗi ngày An đạp xe đến trường với vận tốc 15km/h. Vậy An đi tới trường hết
phút
Khoảng cách từ nhà An đến trường học là 3km, mỗi ngày An đạp xe đến trường với vận tốc 15km/h. Vậy An đi tới trường hết
phút
Áp dụng công thức tính quãng đường: \(t = \dfrac{s}{v}\)
Đổi giờ ra phút: \(a(h) = a.60\) phút
Thời gian An đi từ nhà tới trường là: \(t = \dfrac{s}{v} = \dfrac{3}{{15}} = 0,2\) (giờ) = \(0,2.60\) = \(12\) phút
Thực hiện phép tính sau: \(12,3 + 5,67\) ta được kết quả là
Thực hiện phép tính sau: \(12,3 + 5,67\) ta được kết quả là
\(12,3 + 5,67 = 17,97 \)
Kết quả của phép tính \(\left( { - 12,3} \right) + \left( { - 5,67} \right)\) là
Kết quả của phép tính \(\left( { - 12,3} \right) + \left( { - 5,67} \right)\) là
\(\left( { - 12,3} \right) + \left( { - 5,67} \right) = - 17,97\;\;\)
Thực hiện phép tính \( - 5,5 + 90,67\) ta được kết quả là:
Thực hiện phép tính \( - 5,5 + 90,67\) ta được kết quả là:
\( - 5,5 + 90,67 = 90,67-5,5 = 85,17\;{\rm{ }}\)
Kết quả của phép trừ \(0,008 - 3,9999\) là:
Kết quả của phép trừ \(0,008 - 3,9999\) là:
\(0,008 - 3,9999 = 0,008 + \left( { - 3,9999} \right) = - \left( {3,9999-0,008} \right) = - 3,9919\)
Cho biết một quả chuối nặng 100 g có chứa:
- Chất béo: 0,3 g
- Kali: 0,42 g.
Trong quả chuối đó, khối lượng kali nhiều hơn khối lượng chất béo là
g
Cho biết một quả chuối nặng 100 g có chứa:
- Chất béo: 0,3 g
- Kali: 0,42 g.
Trong quả chuối đó, khối lượng kali nhiều hơn khối lượng chất béo là
g
Tính hiệu của khối lượng kali và khối lượng chất béo.
Khối lượng kali nhiều hơn khối lượng chất béo là: \(0,42 - 0,3 = 0,12\)(g)
Tính một cách hợp lí: \(89,45 + \left( { - 3,28} \right) + 0,55 + \left( { - 6,72} \right)\) ta được kết quả bằng
-
A.
\(80\)
-
B.
\(-80\)
-
C.
\(100\)
-
D.
\(-100\)
Đáp án : A
Áp dụng:
- Tính chất giao hoán: Với mọi a,b thuộc \(\mathbb{Z}\): a + b = b + a.
- Tính chất kết hợp: Với mọi a,b,c thuộc \(\mathbb{Z}\): (a + b) + c = a + (b + c).
\(\begin{array}{l}89,45 + \left( { - 3,28} \right) + 0,55 + \left( { - 6,72} \right)\\ = 89,45 + 0,55 + \left( { - 3,28} \right) + \left( { - 6,72} \right)\\ = \left( {89,45 + 0,55} \right) + \left[ {\left( { - 3,28} \right) + \left( { - 6,72} \right)} \right]\\ = 90 + \left( { - 10} \right)\\ = 90 - 10\\ = 80\end{array}\)
Bạn Nam cao 1,57 m, bạn Linh cao 1,53 m, bạn Loan cao 1,49 m.
Trong ba bạn đó, bạn nào cao nhất? Bạn nào thấp nhất?
-
A.
Bạn Nam cao nhất, bạn Loan thấp nhất
-
B.
Bạn Linh cao nhất, bạn Loan thấp nhất
-
C.
Bạn Nam cao nhất, bạn Linh thấp nhất
-
D.
Bạn Loan cao nhất, bạn Nam thấp nhất
Đáp án: A
So sánh các số thập phân rồi suy ra bạn nào cao nhất? Bạn nào thấp nhất?
Ta thấy: \(1,57 > 1,53 > 1,49\)
=> Bạn Nam cao nhất, bạn Loan thấp nhất.
Chiều cao của bạn cao nhất hơn bạn thấp nhất là bao nhiêu mét?
-
A.
\(0,18\,m\)
-
B.
\(0,08\,m\)
-
C.
\(0,04\,m\)
-
D.
\(0,14\,m\)
Đáp án: B
Tính hiệu chiều cao của bạn cao nhất và thấp nhất.
Chiều cao của bạn cao nhất hơn bạn thấp nhất là: 1,57 - 1,49 = 0,08 (m)
Bác Đồng của ba thanh gỗ: thanh thứ nhất dài 1,85 m, thanh thứ hai dài hơn thanh thứ nhất 10 cm. Độ dài thanh gỗ thứ ba ngắn hơn tổng độ dài hai thanh gỗ đầu tiên là 1,35 m. Thanh gỗ thứ ba mà bác Đồng đã cưa dài bao nhiêu mét?
-
A.
\(1,95\,m\)
-
B.
\(3,8\,m\)
-
C.
\(2,45\,m\)
-
D.
\(2,38\,m\)
Đáp án : C
- Tính chiều dài thanh gỗ thứ hai.
- Tính tổng chiều dài hai thanh gỗ đầu tiên.
=> Tính chiều dài thanh gỗ thứ ba
Đổi \(10 cm = 0,1 m\)
Chiều dài thanh gỗ thứ hai là: \(1,85 + 0,1 = 1,95\) (m)
Tổng chiều dài hai thanh gỗ đầu tiên là: \(1,85 + 1,95 = 3,8\)(m)
Chiều dài thanh gỗ thứ ba là: \(3,8 - 1,35 = 2,45\) (m)
-
A.
\(8,75\)(cm)
-
B.
\(9,75(cm^2)\)
-
C.
\(7,55(cm^2)\)
-
D.
\(9,75\)(cm)
Đáp án : D
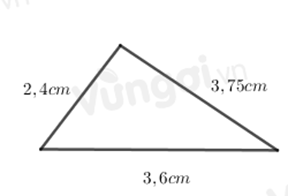
Chu vi tam giác = Tổng độ dài ba cạnh.
Chu vi hình tam giác là: \(2,4 + 3,75 + 3,6 = 9,75\) (cm).
Một số em không quan sát kĩ dẫn đến chọn nhầm đáp án có đơn vị là \(cm^2\)
Thực hiện phép tính: \(\left( { - 4,5} \right) + 3,6 + 4,5 + \left( { - 3,6} \right)\) ta được kết quả là:
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : A
Nhóm thành các tổng hai số đối nhau.
\(\begin{array}{*{20}{l}}{\left( { - 4,5} \right) + 3,6 + 4,5 + \left( { - 3,6} \right)}\\{ = \;{\rm{ }}\left[ {\left( { - 4,5} \right){\rm{ }} + 4,5} \right] + \left[ {3,6 + \left( { - 3.6} \right)} \right]\;}\\{ = {\rm{ }}0 + 0 = 0}\end{array}\)
Thực hiện các phép tính sau: \( - 0,18.\left( { - 1,5} \right)\) ta được kết quả là:
-
A.
\( - 0,27\)
-
B.
\( - 2,7\)
-
C.
\(0,27\)
-
D.
\(2,7\)
Đáp án : C
Tích của hai số thập phân cùng dấu luôn là một số dương
\( - 0,18.\left( { - 1,5} \right) = 0,18.1,5 = 0,27\)
Thực hiện các phép tính sau: \(\left( { - {\rm{ }}45,5} \right).{\rm{ }}0,4\) ta được kết quả là:
-
A.
\(18,2\)
-
B.
\( - 18,2\)
-
C.
\( - 182\)
-
D.
\( - 1,82\)
Đáp án : B
Tích và thương của hai số thập phân khác dấu luôn là một số âm.
\(\left( { - {\rm{ }}45,5} \right).0,4{\rm{ }} = \; - \left( {45,5.0,4} \right) = - 18,2\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;\)
Tính diện tích S của một hình tròn có bán kính \(R = 10{\rm{ }}cm\) theo công thức \(S = \pi {R^2}\) với \(\pi = 3,14\)
-
A.
\(31,4\,\,c{m^2}\)
-
B.
\(314\,c{m^2}\)
-
C.
\(64,8\,c{m^2}\)
-
D.
\(314\,c{m^3}\)
Đáp án : B
Thay \(R,\,\,\pi \) vào công thức \(S = \pi {R^2}\), sau đó thực hiện phép tính.
Diện tích hình tròn là: \(S = 3,{14.10^2} = 314\,c{m^2}\)
Thực hiện các phép tính sau: \(0,15.4,4\) ta được kết quả là:
-
A.
\(6,6\)
-
B.
\(0,66\)
-
C.
\(6,60\)
-
D.
\(0,066\)
Đáp án : B
Tích của hai số thập phân cùng dấu luôn là một số dương
\(0,15.4,4 = 0,66\)
Thực hiện phép tính: \(3,176 - \left( {2,104 + 1,18} \right)\) ta được kết quả là
Thực hiện phép tính: \(3,176 - \left( {2,104 + 1,18} \right)\) ta được kết quả là
Thực hiện phép tính trong ngoặc trước, sau đó thực hiện phép trừ.
\(3,176 - \left( {2,104 + 1,18} \right) = 3,176 - 3,284 = - 0,108\)
Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là
\(cm^2\)
Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là
\(cm^2\)
Diện tích của hình chữ nhật bằng chiều dài nhân chiều rộng.
Diện tích của hình chữ nhật đó là:
\(31,21.22,52 = 702,8492\)(cm2)

Khối lượng vitamin C trung bình trong một quả ớt chuông là 0,135 g, còn trong một quả cam là 0,045 g. Khối lượng vitamin C trong quả ớt chuông gấp bao nhiêu lần trong quả cam?
-
A.
2 lần
-
B.
3 lần
-
C.
4 lần
-
D.
5 lần
Đáp án : B
Lấy khối lượng vitamin C trong quả ớt chuông chia cho khối lượng lượng vitamin C trong quả cam.
Khối lượng vitamin C trong quả ớt chuông gấp số lần trong quả cam là:
0,135 : 0,045 =3 ( lần)
Đáp số: 3 lần.
Tính chu vi của một hình tròn có bán kính R = 1,25 m theo công thức C = \(2\pi R\) với \(\pi \) = 3,142.
-
A.
7,855 m
-
B.
7,855 m2
-
C.
7,585 m
-
D.
7,558 m
Đáp án : A
Áp dụng công thức C = \(2\pi R\).
Chu vi của hình tròn đó là:
\(C = 2πR = 2.3,142.1,25 = 7,855\) (m)
Đáp số: 7,855 m

Tìm \(y\), biết: \(135,2 - y = 52,53 + 16,7\).
A. \(y = 65,97\)
B. \(y = 66,2\)
C. \(y = 82,67\)
D. \(y = 204,43\)
A. \(y = 65,97\)
- Tính giá trị của vế phải: \(52,53 + 16,7 = 69,23\).
- \(y\) ở vị trí số trừ nên để tìm \(y\) ta lấy số bị trừ trừ đi hiệu.
Ta có:
\(\begin{array}{l}135,2 - y = 52,53 + 16,7\\135,2 - y = 69,23\\ y = 135,2 - 69,23\\ y = 65,97\end{array}\)
Vậy \(y = 65,97\).

Điền số thích hợp vào ô trống để tính bằng cách thuận tiện:
\(245,18 - 81,359 - 17,641 + 113,82\)
\( = (245,18 + \)
\( ) \, - \,(81,359 + \)
\( ) \)
\( = \)
\(- \)
\( =\)
\(245,18 - 81,359 - 17,641 + 113,82\)
\( = (245,18 + \)
\( ) \, - \,(81,359 + \)
\( ) \)
\( = \)
\(- \)
\( =\)
Ta có: $a - b - c + d\; = \;\left( {a + \;d} \right) - \left( {b + c} \right)$.
Nhận thấy \(18 + 82 = 100;\,\,\,359 + 641 = 1000\) nên ta nhóm các số thập phân có phần thập phân cộng với nhau là số tròn chục, tròn trăm, tròn nghìn, ...
Ta có:
\(\begin{array}{l}245,18 - 81,359 - 17,641 + 113,82\\ = (245,18 + 113,82) - (81,359 + 17,641)\\ = 359 - 99\\ = 260\end{array}\)
Vậy số thích hợp điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải lần lượt là \(113,82 \,;\,\, 17,641\,;\,\, 359 \,;\,\, 99 \,;\,\,260\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một cửa hàng có \(58,5kg\) gạo nếp, số gạo tẻ nhiều hơn gạo nếp \(33,8kg\). Vậy cửa hàng có tất cả
tạ gạo.
Một cửa hàng có \(58,5kg\) gạo nếp, số gạo tẻ nhiều hơn gạo nếp \(33,8kg\). Vậy cửa hàng có tất cả
tạ gạo.
- Tìm số gạo tẻ ta lấy số gạo nếp cộng với \(33,8kg\).
- Tìm tổng số gạo ta lấy số gạo nếp cộng với số gạo tẻ.
- Đổi số gạo của cửa hàng sang đơn vị tạ.
Cửa hàng có số ki-lô-gam gạo tẻ là:
\(58,5 + 33,8 = 92,3\;(kg)\)
Cửa hàng có tất cả số ki-lô-gam gạo là:
\(58,5 + 92,3 = 150,8\;(kg)\)
\(150,8kg = 1,508\) tạ.
Đáp số: \(1,508\) tạ
Học sinh cần nhớ bảng đơn vị đo khối lượng và cách viết số đo khối lượng dưới dạng số thập phân.

\(24,225km + 818m - 67,9hm = ...km\).
Số thích hợp điền vào chỗ chấm là:
A. \(18,253\)
B. \(25,615\)
C. \(31,726\)
D. \(774,325\)
A. \(18,253\)
Đổi các số đo về cùng đơn vị đo là \(km\) rồi tính lần lượt từ trái sang phải.
Ta có:
\(\begin{array}{l}24,225km + 818m - 67,9hm \\= 24,225km + 0,818km - 6,79km\\ = 25,043km - 6,79km \\= 18,253km\end{array}\)
Vậy số thích hợp điền vào chỗ chấm là \(18,253\).
Học sinh cần nhớ bảng đơn vị đo độ dài và cách viết số đo độ dài dưới dạng số thập phân.
Điền số thích hợp vào ô trống:
Cho đường gấp khúc ABCD như hình vẽ:

Độ dài đường gấp khúc đó là
\( m.\)
Cho đường gấp khúc ABCD như hình vẽ:

Độ dài đường gấp khúc đó là
\( m.\)
- Đổi các số đo về cùng đơn vị đo là \(m\).
- Để tìm độ dài đường gấp khúc ta lấy độ dài của các đoạn thẳng trong đường gấp khúc cộng lại với nhau.
Đổi : \(48cm = 0,48m; \quad 7,7dm = 0,77m\)
Độ dài đường gấp khúc ABCD là:
\(0,48 + 0,77 + 1,02 = 2,27(m)\)
Đáp số: \(2,27m\).
Học sinh cần nhớ bảng đơn vị đo độ dài và cách viết số đo độ dài dưới dạng số thập phân.

$385,18$ trừ đi hiệu của $207,4$ và $91,28$ rồi cộng với $115$ được kết quả là:
A. \(201,5\)
B. \(231,12\)
C. \(384,06\)
D. \(616,33\)
C. \(384,06\)
Từ dữ kiện đề bài cho ta lập biểu thức thích hợp rồi tính giá trị biểu thức đó.
Từ đề bài ta có biểu thức: \(385,18 - (207,4 - 91,28) + 115\).
Tính giá trị biểu thức trên ta có:
\(\begin{array}{l}385,18 - (207,4 - 91,28) + 115\\ = 385,18 - 116,12 + 115\\ = 269,06 + 115\\ = 384,06\end{array}\)
Luyện tập và củng cố kiến thức Bài 8: Ước lượng và làm tròn số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Tỉ số. Tỉ số phần trăm Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Hai bài toán về phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương V Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Số thập phân Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép nhân, phép chia phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Phép nhân, phép chia phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng, phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Phép cộng, phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Hỗn số dương Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: So sánh phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phân số với tử và mẫu là số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Phân số với tử và mẫu là số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết


















Danh sách bình luận