Bài tập trắc nghiệm Toán 6 - Cánh diều có đáp án Bài tập trắc nghiệm Chương 2. Số nguyên

Trắc nghiệm Bài 2: Tập hợp các số nguyên Toán 6 Cánh diều

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Tập hợp các số nguyên kí hiệu là

A.

$N$
B.

${N^*}$
C.

$Z$
D.

${Z^*}$

Câu 2 :

Số đối của số $ - 3$ là

A.

$3$
B.

$ - 3$
C.

$2$
D.

$4$

Câu 3 :

Chọn câu đúng

A.

$ - 6 \in N$
B.

$9 \notin Z$
C.

$ - 9 \in N$
D.

$ - 10 \in Z$

Câu 4 :

Điểm $6$ cách điểm $2$ bao nhiêu đơn vị?

A.

$3$
B.

$5$
C.

$2$
D.

$4$

Câu 5 :

Cho tập hợp $A = \left\{ { - 3;2;0; - 1;5;7} \right\}$. Viết tập hợp $B$ gồm các phần tử là số đối của các phần tử trong tập hợp $A.$

A.

$B = \left\{ {3; - 2;0;1; - 5; - 7} \right\}$
B.

$B = \left\{ {3; - 2;0; - 5; - 7} \right\}$
C.

$B = \left\{ {3; - 2;0;1; - 5;7} \right\}$
D.

$B = \left\{ { - 3;2;0;1; - 5; - 7} \right\}$

Câu 6 :

Số cách số $ - 2$ sáu đơn vị theo chiều dương là?

A.

$6$
B.

$ - 8$
C.

$4$
D.

$5$

Câu 7 :

Trong các số: $ - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}$ có bao nhiêu số là số nguyên.

A.
$1$
B.
$2$
C.
$3$
D.
$4$

Câu 8 :

Khẳng định nào sau đây đúng?

A.
Số $0$ vừa là số nguyên dương vừa là số nguyên âm.
B.
Số $0$ là số nguyên dương.
C.
Số $0$ là số nguyên âm.
D.
Tập hợp số nguyên bao gồm số nguyên âm, số nguyên dương và số 0.

Câu 9 : Điểm $x$ trong hình sau đây biểu diễn số nguyên nào?

A.
$ - 2$
B.
$4$
C.
$3$
D.
$ - 3$

Câu 10 :

Điểm $ - 2$ cách điểm $3$ bao nhiêu đơn vị?

A.

$5$
B.

$2$
C.

$1$
D.

$8$

Câu 11 : Nhiệt kế chỉ bao nhiêu độ trong hình dưới đây?

A.
${8^o}C$
B.
$ - {3^o}C$
C.
${3^o}C$
D.
${6^o}C$

Câu 12 : Số đối của -78 là:

A.
$87$
B.
$ - 87$
C.
$ - 78$
D.
$78$

Câu 13 : Trong các phát biểu sau, phát biểu nào đúng?

A.
Số đối của một số nguyên dương là một số nguyên âm.
B.
Số $0$ không có số đối.
C.
Số đối của mọi số nguyên dương đều là số nguyên dương.
D.
Số đối của mọi số nguyên âm đều là số nguyên âm.

Lời giải và đáp án

Câu 1 :

Tập hợp các số nguyên kí hiệu là

A.

$N$
B.

${N^*}$
C.

$Z$
D.

${Z^*}$

Đáp án : C

Lời giải chi tiết :

Tập hợp các số nguyên kí hiệu là $Z.$

Câu 2 :

Số đối của số $ - 3$ là

A.

$3$
B.

$ - 3$
C.

$2$
D.

$4$

Đáp án : A

Phương pháp giải :

- Sử dụng: Số đối của $a$ là $ - a.$

Lời giải chi tiết :

Ta có số đối của số $ - 3$ là $3.$

Câu 3 :

Chọn câu đúng

A.

$ - 6 \in N$
B.

$9 \notin Z$
C.

$ - 9 \in N$
D.

$ - 10 \in Z$

Đáp án : D

Phương pháp giải :

Tập hợp số nguyên bao gồm số nguyên âm, số $0$ và số nguyên dương.
Tập hợp số nguyên kí hiệu là: $Z$
Tập hợp số tự nhiên kí hiệu là: $N$

Lời giải chi tiết :

Ta có $ - 10 \in Z$ vì $ - 10$ là số nguyên âm nên D đúng.

Câu 4 :

Điểm $6$ cách điểm $2$ bao nhiêu đơn vị?

A.

$3$
B.

$5$
C.

$2$
D.

$4$

Đáp án : D

Phương pháp giải :

- Sử dụng kiến thức về trục số để xác định khoảng cách từ điểm $6$ đến điểm $2$.

Lời giải chi tiết :

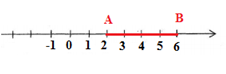
Điểm $6$ cách điểm $2$ là bốn đơn vị

Câu 5 :

Cho tập hợp $A = \left\{ { - 3;2;0; - 1;5;7} \right\}$. Viết tập hợp $B$ gồm các phần tử là số đối của các phần tử trong tập hợp $A.$

A.

$B = \left\{ {3; - 2;0;1; - 5; - 7} \right\}$
B.

$B = \left\{ {3; - 2;0; - 5; - 7} \right\}$
C.

$B = \left\{ {3; - 2;0;1; - 5;7} \right\}$
D.

$B = \left\{ { - 3;2;0;1; - 5; - 7} \right\}$

Đáp án : A

Phương pháp giải :

+ Tìm số đối của mỗi phần tử thuộc tập hợp $A$ bằng cách sử dụng: Số đối của $a$ là $ - a.$

+ Từ đó viết tập hợp $B.$

Lời giải chi tiết :

Số đối của $ - 3$ là $3$; số đối của $2$ là $ - 2;$ số đối của $0$ là $0;$số đối của $ - 1$ là 1; số đối của $5$ là $ - 5;$ số đối của $7$ là $ - 7.$

Nên tập hợp $B = \left\{ {3; - 2;0;1; - 5; - 7} \right\}$

Câu 6 :

Số cách số $ - 2$ sáu đơn vị theo chiều dương là?

A.

$6$
B.

$ - 8$
C.

$4$
D.

$5$

Đáp án : C

Phương pháp giải :

Điểm nằm cách điểm A theo chiều dương tức là điểm đó nằm bên tay phải điểm A
Điểm nằm cách điểm A theo chiều âm tức là điểm đó nằm bên trái điểm A

Lời giải chi tiết :

Ta đếm về bên phải số $ - 2$ sáu đơn vị được số $4$ ( hay $ + 4$ )
Vậy số cách số $ - 2$ sáu đơn vị theo chiều dương là: $4$ ( hay $ + 4$)

Câu 7 :

Trong các số: $ - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}$ có bao nhiêu số là số nguyên.

A.
$1$
B.
$2$
C.
$3$
D.
$4$

Đáp án : C

Phương pháp giải :

Tập hợp số gồm các số nguyên âm, số $0$ và các số nguyên dương được gọi là tập hợp số nguyên.

Lời giải chi tiết :

Các số là số nguyên là: $ - 2;\,\,4;\, - 100$.

Vậy có $3$ số là số nguyên.

Câu 8 :

Khẳng định nào sau đây đúng?

A.
Số $0$ vừa là số nguyên dương vừa là số nguyên âm.
B.
Số $0$ là số nguyên dương.
C.
Số $0$ là số nguyên âm.
D.
Tập hợp số nguyên bao gồm số nguyên âm, số nguyên dương và số 0.

Đáp án : D

Phương pháp giải :

Tập hợp số gồm các số nguyên âm, số $0$ và các số nguyên dương được gọi là tập hợp số nguyên.

Lời giải chi tiết :

Tập hợp số nguyên bao gồm số nguyên âm, số nguyên dương và số 0.

$ \Rightarrow A,\,B,\,C$ sai.

Tập hợp số nguyên bao gồm số nguyên âm, số nguyên dương và số 0.

Câu 9 : Điểm $x$ trong hình sau đây biểu diễn số nguyên nào?

A.
$ - 2$
B.
$4$
C.
$3$
D.
$ - 3$

Đáp án : D

Phương pháp giải :

Đếm khoảng cách từ điểm $x$ đến điểm $0$, thêm dấu “-” vào số vừa tìm được.

Lời giải chi tiết :

Điểm $x$ trong hình biểu diễn số $ - 3$.

Câu 10 :

Điểm $ - 2$ cách điểm $3$ bao nhiêu đơn vị?

A.

$5$
B.

$2$
C.

$1$
D.

$8$

Đáp án : A

Phương pháp giải :

Dựa vào trục số để xác định
Nếu điểm này cách điểm kia theo chiều từ trái sang phải gọi là chiều dương, chiều từ phải sang trái gọi là chiều âm của trục số.

Lời giải chi tiết :

Quan sát trục số ta thấy: Điểm $ - 2$ cách điểm $3$ là $5$ đơn vị.

Câu 11 : Nhiệt kế chỉ bao nhiêu độ trong hình dưới đây?

A.
${8^o}C$
B.
$ - {3^o}C$
C.
${3^o}C$
D.
${6^o}C$

Đáp án : B

Phương pháp giải :

Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.

Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.

Lời giải chi tiết :

Quan sát hình ta thấy vạch đỏ ở điểm $ - 3$, vậy nhiệt kế chỉ $ - {3^o}C$.

Câu 12 : Số đối của -78 là:

A.
$87$
B.
$ - 87$
C.
$ - 78$
D.
$78$

Đáp án : D

Phương pháp giải :

Số đối của số $ - a$ là $a$.

Lời giải chi tiết :

Số đối của $ - 78$ là $78$.

Câu 13 : Trong các phát biểu sau, phát biểu nào đúng?

A.
Số đối của một số nguyên dương là một số nguyên âm.
B.
Số $0$ không có số đối.
C.
Số đối của mọi số nguyên dương đều là số nguyên dương.
D.
Số đối của mọi số nguyên âm đều là số nguyên âm.

Đáp án : A

Phương pháp giải :

Số đối của số $a$ là $ - a$.

Lời giải chi tiết :

- Số đối của một số nguyên dương là một số nguyên âm => C sai, A đúng

- Số đối của một số nguyên âm là một số nguyên dương => D sai.

- Số đối của $0$ là $0$ => B sai.

Trắc nghiệm Các dạng toán về tập hợp các số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về tập hợp các số nguyên học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Thứ tự trong tập hợp số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Thứ tự trong tập hợp số nguyên học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Các dạng toán về thứ tự trong tập hợp số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về thứ tự trong tập hợp số nguyên học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 3: Phép cộng các số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 3: Phép cộng các số nguyên học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 4: Phép trừ các số nguyên. Quy tắc dấu ngoặc Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 4: Phép trừ các số nguyên. Quy tắc dấu ngoặc học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Các dạng toán về phép cộng, phép trừ các số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về phép cộng, phép trừ các số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Các dạng toán về phép cộng, phép trừ các số nguyên (tiếp) Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về phép cộng, phép trừ các số nguyên (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 5,6: Phép nhân, phép chia các số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 5,6: Phép nhân, phép chia các số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Các dạng toán về phép nhân, phép chia các số nguyên Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về phép nhân, phép chia các số nguyên học Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Các dạng toán về phép nhân, phép chia các số nguyên (tiếp) Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Các dạng toán về phép nhân, phép chia các số nguyên (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài tập cuối chương II Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài tập cuối chương II Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 1: Số nguyên âm Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 1: Số nguyên âm Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết