Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Làm đề thiCâu hỏi 1 :
Cho số phức \(z = - 2 + 3i\). Số phức liên hợp của \({\rm{z}}\) là
- A \(\bar z = - 2 - 3i\).
- B \(\bar z = 2 - 3i\).
- C \(\bar z = \sqrt {13} \).
- D \(\bar z = 3 - 2i\)
Đáp án: A
Phương pháp giải:
Số phức liên hợp của \(z = a + bi\) là \(\overline z = a - bi\)
Lời giải chi tiết:
\(\bar z = - 2 - 3i\)
Câu hỏi 2 :
Gọi \((H)\) là hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = \frac{4}{{\rm{x}}}\), trục hoành và các đường thằng \(x = 1,x = 4\). Tính thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục hoành,
- A \(12\pi \).
- B \(6\pi \).
- C \(16\pi \).
- D \(4\pi \)
Đáp án: A
Phương pháp giải:
\(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
\(V = \pi \int\limits_1^4 {{{\left( {\frac{4}{x}} \right)}^2}dx} = 12\pi \)
Câu hỏi 3 :
Tìm tham số thực \(m\) để số phức \(z = 1 - {(m - i)^2}\) là một số thuần ảo.
- A \(m = \pm \sqrt 2 \).
- B \(m = \sqrt 3 \).
- C \(m = 0\).
- D \(m = \pm \sqrt 3 \).
Đáp án: A
Phương pháp giải:
\(\left( {a + bi} \right) \pm \left( {c + di} \right)\)\( = \left( {a \pm c} \right) + \left( {b \pm d} \right)i\)
\(\left( {a + bi} \right).\left( {c + di} \right)\)\( = \left( {ac - bd} \right) + \left( {ad + bc} \right)i\)
Số phức z là số thuần ảo nếu phần thực bằng 0.
Lời giải chi tiết:
\(\begin{array}{l}z = 1 - {(m - i)^2} = 1 - \left( {{m^2} - 1 - 2m.i} \right)\\ = 2 - {m^2} + 2mi\end{array}\)
Để z là số thuần ảo thì \(2 - {m^2} = 0 \Leftrightarrow m = \pm \sqrt 2 \)
Câu hỏi 4 :
Biết \(\int {\frac{{{{\ln }^2}x}}{x}} dx = a{\ln ^3}x + C(a \in \mathbb{Q})\). Tìm khẳng định đúng.
- A \(a \in \left( { - 1;\frac{1}{2}} \right)\).
- B \(a \in \left( {\frac{1}{2};2} \right)\).
- C \(a \in ( - 2; - 1)\).
- D \(a \in (2;4)\).
Đáp án: A
Phương pháp giải:
Đặt \(\ln x = t \Rightarrow dt = \frac{1}{x}dx\)
Lời giải chi tiết:
Đặt \(\ln x = t \Rightarrow dt = \frac{1}{x}dx\)
\(\int {\frac{{{{\ln }^2}x}}{x}} dx = \int {{t^2}dt} = \frac{{{t^3}}}{3} + C\)\( \Rightarrow a = \frac{1}{3} \in \left( { - 1;\frac{1}{2}} \right)\)
Câu hỏi 5 :
Mệnh đề nào dưới đây đúng ?
- A \(\int {\frac{1}{{{{\sin }^2}x}}} \;{\rm{d}}x = - \tan x + C\).
- B \(\int {\frac{1}{{{{\sin }^2}x}}} \;{\rm{d}}x = \tan x + C\).
- C \(\int {\frac{1}{{{{\sin }^2}x}}} \;{\rm{d}}x = - \cot x + C\).
- D \(\int {\frac{1}{{{{\sin }^2}x}}} \;{\rm{d}}x = \cot x + C\).
Đáp án: C
Phương pháp giải:
Sử dụng bảng nguyên hàm cơ bản.
Lời giải chi tiết:
\(\int {\frac{1}{{{{\sin }^2}x}}} \;{\rm{d}}x = - \cot x + C\)
Câu hỏi 6 :
Một vật chuyển động với vận tốc \(v(t)({\rm{m}}/{\rm{s}})\) và có gia tốc \(a(t) = \frac{3}{{t + 1}}\left( {m/{s^2}} \right)\). Vận tốc ban đầu của vật là \(6(m/s)\). Hỏi vận tốc của vật sau 10 giây là bao nhiêu ?
- A \(3\ln 11 - 6\).
- B \(3\ln 6 + 6\).
- C \(3\left( {\ln \frac{{11}}{7}} \right)\).
- D \(3\ln 11 + 6\).
Đáp án: D
Phương pháp giải:
\(a\left( t \right) = v'\left( t \right)\)
Lời giải chi tiết:
\(v\left( t \right) = \int {a\left( t \right)dt} = \int {\frac{3}{{t + 1}}dt} \)\( = 3\ln \left| {t + 1} \right| + C\)
\(v\left( 0 \right) = 6 \Rightarrow 3\ln 1 + C = 6\)\( \Rightarrow C = 6\)
\(\begin{array}{l} \Rightarrow v\left( t \right) = 3\ln \left| {t + 1} \right| + 6\\ \Rightarrow v\left( {10} \right) = 3\ln 11 + 6\end{array}\)
Câu hỏi 7 :
Trong không gian Oxyz, cho hai điểm \(A(1;2;3),B(3;0;1)\). Diện tích của mặt cầu \((S)\) có đường kính AB bằng
- A \(3\pi \)
- B \(9\pi \).
- C \(12\pi \)
- D \(6\pi \).
Đáp án: C
Phương pháp giải:
Bán kính \(R = \frac{{AB}}{2}\)
Độ dài đoạn thẳng AB: \(\sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Diện tích mặt cầu bán kính R: \(S = 4\pi {R^2}\)
Lời giải chi tiết:
\(R = \frac{{AB}}{2} = \frac{{\sqrt {{2^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} }}{2}\)\( = \sqrt 3 \)
\(S = 4\pi {R^2} = 12\pi \)
Câu hỏi 8 :
Trong không gian Oxyz, phương trình của mặt cầu \((S)\) có tâm \(O\) và bán kính \(R = 2\) là
- A \({x^2} + {y^2} + {z^2} = 2\).
- B \({x^2} + {y^2} + {z^2} = 4\).
- C \({(x - 2)^2} + {y^2} + {z^2} = 4\).
- D \({x^2} + {y^2} + {(z - 2)^2} = 4\).
Đáp án: B
Phương pháp giải:
Mặt cầu tâm \(I\left( {{x_0};{y_0};{z_0}} \right)\) bán kính R: \({\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {R^2}\)
Lời giải chi tiết:
Mặt cầu tâm \(O\left( {0;0;0} \right)\) bán kính R=2 có phương trình là:
\({x^2} + {y^2} + {z^2} = 4\)
Câu hỏi 9 :
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A(1;2;3)\) lên mặt phẳng (Oxz) là
- A \(E(0;2;0)\).
- B \(D(1;2;0)\)
- C \(C(0;2;3)\).
- D \(B(1;0;3)\).
Đáp án: D
Phương pháp giải:
Hình chiếu của \(M\left( {x;y;z} \right)\) lên (Oxz) là \(M'\left( {x;0;z} \right)\)
Lời giải chi tiết:
Hình chiếu của điểm \(A(1;2;3)\) lên mặt phẳng (Oxz) là:
\(B(1;0;3)\)
Câu hỏi 10 :
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 1 \right) - f\left( 0 \right) = 2\). Tích phân \(I = \int\limits_0^1 {f'\left( x \right)dx} \) bằng
- A \(I = 2\)
- B \(I = - 1\)
- C \(I = 0\)
- D \(I = 1\)
Đáp án: A
Phương pháp giải:
\(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\)
Lời giải chi tiết:
\(I = \int\limits_0^1 {f'\left( x \right)dx} = f\left( 1 \right) - f\left( 0 \right) = 2\)
Câu hỏi 11 :
Cho hàm số \(y = f(x)\) liên tục trên [a ; b]. Viết công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục Ox và các đường thẳng \(x = a,x = b(a < b)\).
- A \(S = \int_a^b f (x){\rm{d}}x\).
- B \(S = \int_a^b | f(x)|{\rm{d}}x\).
- C \(S = - \int_a^b f (x){\rm{d}}x\).
- D \(S = \pi \int\limits_a^b {|f(x)|{\rm{d}}x} \).
Đáp án: B
Phương pháp giải:
Công thức tính diện tích hình phẳng.
Lời giải chi tiết:
\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Câu hỏi 12 :
Biết \(\int_1^2 f (x){\rm{d}}x = 3\). Giá trị của \(\int\limits_1^2 {\left[ {2f\left( x \right)} \right]dx} \) bằng
- A 1 .
- B 6 .
- C 4
- D 5 .
Đáp án: B
Phương pháp giải:
\(\int\limits_a^b {\left[ {k.f\left( x \right)} \right]dx} = k.\int\limits_a^b {f\left( x \right)dx} \)
Lời giải chi tiết:
\(\int\limits_1^2 {\left[ {2f\left( x \right)} \right]dx} \)\( = 2.\int_1^2 f (x){\rm{d}}x = 2.3 = 6\)
Câu hỏi 13 :
Trong không gian Oxyz, phương trình đường thẳng đi qua điểm \(A(3; - 2;4)\) và có vecto chỉ phương \(\vec u = (2; - 1;6)\) là
- A \(\frac{{x - 3}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 4}}{6}\).
- B \(\frac{{x + 3}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z + 4}}{6}\).
- C \(\frac{{x - 3}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 4}}{6}\).
- D \(\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 6}}{4}\).
Đáp án: A
Phương pháp giải:
Đường thẳng qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow u = \left( {a;b;c} \right)\) làm vecto chỉ phương có phương trình chính tắc: \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\)
Lời giải chi tiết:
Phương trình đường thẳng đi qua điểm \(A(3; - 2;4)\) và có vecto chỉ phương \(\vec u = (2; - 1;6)\) là: \(\frac{{x - 3}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 4}}{6}\)
Câu hỏi 14 :
Tìm \(\frac{{2 + 3i}}{{1 + i}}\).
- A \(\frac{{ - 1}}{2} + \frac{5}{2}i\).
- B \(\frac{3}{2} + \frac{5}{2}i\).
- C \(\frac{5}{2} + \frac{1}{2}i\).
- D \(\frac{{ - 1}}{2} + \frac{1}{2}i\).
Đáp án: C
Phương pháp giải:
Sử dụng MTCT, bật Mode 2.
Lời giải chi tiết:
\(\frac{{2 + 3i}}{{1 + i}} = \frac{5}{2} + \frac{1}{2}i\)
Câu hỏi 15 :
Trong không gian Oxyz, cho mặt phẳng \((P):x - y + 2z - 3 = 0\). Vectơ nào sau đây là vectơ chỉ phương của đường thẳng vuông góc với mặt phẳng \((P)\) ?
- A \(\vec b = (1; - 1; - 3)\).
- B \(\vec v = (1;1; - 2)\).
- C \(\vec u = ( - 1; - 1;2)\).
- D \(\vec a = (1; - 1;2)\).
Đáp án: D
Phương pháp giải:
\(\overrightarrow {{n_{\left( P \right)}}} \bot \left( P \right)\).
Đường thẳng vuông góc với mặt phẳng thì vecto chỉ phương của đường thẳng vuông góc với mặt phẳng đó.
Lời giải chi tiết:
\(\overrightarrow a = \overrightarrow {{n_{\left( P \right)}}} \) nên \(\vec a = (1; - 1;2)\) là một vecto chỉ phương của đường thẳng vuông góc với (P).
Câu hỏi 16 :
Cho hai số phức \({z_1} = 1 + i\) và \({z_2} = a - bi\). Tìm phần ảo của số phức \({z_1} + {z_2}\).
- A \(1 - b\).
- B \((1 - b)i\).
- C \(1 + b\).
- D \(1 + a\).
Đáp án: A
Phương pháp giải:
\(\left( {a + bi} \right) \pm \left( {c + di} \right)\)\( = \left( {a \pm c} \right) + \left( {b \pm d} \right)i\)
Lời giải chi tiết:
\({z_1} + {z_2} = \left( {1 + i} \right) + \left( {a - bi} \right)\)\( = \left( {1 + a} \right) + \left( {1 - b} \right)i\)
Câu hỏi 17 :
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A(0; - 1;0)\) và có vectơ pháp tuyến \(\vec n = (3; - 1; - 2)\) có phương trình là
- A \(x - 2y + 2z - 1 = 0.\)
- B \(x - 2y + 2z + 1 = 0\)
- C \(3x - y - 2z - 1 = 0\).
- D \(3x - y - 2z + 1 = 0\).
Đáp án: C
Phương pháp giải:
Mặt phẳng qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b;c} \right)\) làm vecto pháp tuyến có phương trình: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\)
Lời giải chi tiết:
\(3.x - \left( {y + 1} \right) - 2z = 0\)\( \Leftrightarrow 3x - y - 2z - 1 = 0\)
Câu hỏi 18 :
Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y = f(x),x = a,x = b(a < b)\) và trục Ox. Khi quay \((H)\) quanh trục Ox ta được một khối tròn xoay có thể tích tính bằng công thức nào sau đây?
- A \(V = \pi \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
- B \(V = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
- C \(V = \pi \int\limits_a^b {f\left( x \right)dx} \)
- D \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Đáp án: D
Phương pháp giải:
Ứng dụng tích phân tính thể tích.
Lời giải chi tiết:
\(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Câu hỏi 19 :
Gọi a, b lần lượt là phần thực và phần ảo của số phức \(z = \frac{1}{4} + \frac{{\sqrt 2 }}{2}i\). Tính tỉ số \(\frac{a}{b}\).
- A \( - \sqrt 2 \)
- B \(\frac{{\sqrt 2 }}{4}\)
- C \(\sqrt 2 \)
- D \(\frac{1}{{\sqrt 2 }}\)
Đáp án: B
Phương pháp giải:
Xác định a, b.
Tính \(\frac{a}{b}\)
Lời giải chi tiết:
Phần thực là \(\frac{1}{4}\), phần ảo là \(\frac{{\sqrt 2 }}{2}\).
\(\frac{a}{b} = \frac{{\frac{1}{4}}}{{\frac{{\sqrt 2 }}{2}}} = \frac{1}{4}.\sqrt 2 = \frac{{\sqrt 2 }}{4}\)
Câu hỏi 20 :
Cho số phức z thỏa mãn \(\left( {3 - i} \right)z - 2 = 6i\). Môđun của số phức \(w = 2z - 3\).
- A \(\left| w \right| = \sqrt 7 \)
- B \(\left| w \right| = 5\)
- C \(\left| w \right| = \sqrt {13} \)
- D \(\left| w \right| = 25\)
Đáp án: B
Phương pháp giải:
Tìm z bằng MTCT: bật Mode 2.
Tính |w|.
Lời giải chi tiết:
\(\left( {3 - i} \right)z - 2 = 6i \Rightarrow z = \frac{{2 + 6i}}{{3 - i}} = 2i\)
\(\begin{array}{l}w = 2z - 3 = 2.2i - 3 = - 3 + 4i\\ \Rightarrow \left| w \right| = 5\end{array}\)
Câu hỏi 21 :
Cho số phức \(z = \frac{{a + 2i}}{{1 - i}}\left( {a \in \mathbb{R}} \right)\). Hỏi có bao nhiêu số thực a thỏa mãn \(\left| z \right| = \sqrt {10} \).
- A 2 .
- B 1 .
- C 4 .
- D 3 .
Đáp án: A
Phương pháp giải:
\(\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}\)
Lời giải chi tiết:
\(\begin{array}{l}z = \frac{{a + 2i}}{{1 - i}} \Rightarrow \left| z \right| = \frac{{\left| {a + 2i} \right|}}{{\left| {1 - i} \right|}} = \frac{{\sqrt {{a^2} + 4} }}{{\sqrt 2 }} = \sqrt {10} \\ \Rightarrow \sqrt {{a^2} + 4} = \sqrt {20} \\ \Leftrightarrow {a^2} + 4 = 20\\ \Leftrightarrow {a^2} = 16\\ \Leftrightarrow a = \pm 4\end{array}\)
=> Có 2 giá trị thỏa mãn bài toán.
Câu hỏi 22 :
Nguyên hàm \(F(x)\) của hàm số \(f(x) = {x^2} - 2\) là
- A \(F(x) = \frac{{{x^3}}}{3} - 2x + C\).
- B \(F(x) = \frac{{{x^3}}}{3} - x + C\).
- C \(F(x) = \frac{{{x^3}}}{3} - {x^2} + C\).
- D \(F(x) = 2x + C\).
Đáp án: A
Phương pháp giải:
\(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\)
Lời giải chi tiết:
\(F(x) = \int {\left( {{x^2} - 2} \right)dx} = \frac{{{x^3}}}{3} - 2x + C\)
Câu hỏi 23 :
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = - 1 + 3t}\\{z = 2 - t}\end{array}} \right.\) . Điểm nào dưới đây thuộc \(\Delta \)?
- A \(C( - 1;1; - 2)\).
- B \(A( - 1; - 4;3)\).
- C \(B(2;3; - 1)\).
- D \(D(2; - 2;4)\)
Đáp án: B
Phương pháp giải:
Cho t=-1. Thay vào hệ phương trình tìm x,y,z.
Lời giải chi tiết:
Thay t=-1 vào hệ phương trình ta được x=-1;y=-4;z=3
Câu hỏi 24 :
Tất cả các nghiệm phức của phương trình \({z^2} + 5 = 0\) là
- A \( \pm 5\).
- B \( \pm 5i\).
- C \( \pm \sqrt 5 \).
- D \( \pm \sqrt 5 i\).
Đáp án: D
Phương pháp giải:
Sử dụng MTCT, Mode 5 -> 3. Bấm hệ số vào tìm nghiệm.
Lời giải chi tiết:
\({z^2} + 5 = 0 \Leftrightarrow z = \pm \sqrt 5 i\)
Câu hỏi 25 :
Trong mặt phẳng Oxy, điểm biểu diễn của số phức \(z = 2 + 3i\) là
- A \(M(3;2)\).
- B \(M( - 2; - 3)\).
- C \(M(3; - 2)\).
- D \(M(2;3)\).
Đáp án: D
Phương pháp giải:
Điểm biểu diễn số phức \(z = a + bi\) là: \(M\left( {a;b} \right)\)
Lời giải chi tiết:
Điểm biểu diễn của số phức \(z = 2 + 3i\) là \(M(2;3)\)
Câu hỏi 26 :
Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm \(A(3; - 1;2)\) và \(B(4;1;0)\) là
- A \(\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 2}}{{ - 2}}\).
- B \(\frac{{x + 3}}{1} = \frac{{y - 1}}{2} = \frac{{z + 2}}{{ - 2}}\).
- C \(\frac{{x - 3}}{4} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 2}}{1}\).
- D \(\frac{{x - 1}}{3} = \frac{{y - 2}}{{ - 1}} = \frac{{z + 2}}{2}\).
Đáp án: A
Phương pháp giải:
Tìm \(\overrightarrow {AB} \).
Phương trình đường thẳng đi qua hai điểm A,B nhận \(\overrightarrow {AB} \) làm vecto chỉ phương.
Lời giải chi tiết:
\(\overrightarrow {AB} = \left( {1;2; - 2} \right)\)
Phương trình đường thẳng đi qua hai điểm \(A(3; - 1;2)\) và \(B(4;1;0)\) là:
\(\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 2}}{{ - 2}}\)
Câu hỏi 27 :
Cho \(\int_1^2 f (x)dx = 2,\int_3^2 f (x)dx = 5\). Tính \(\int_0^2 f (x + 1)dx\).
- A 3 .
- B \( - 3\).
- C 4 .
- D 7 .
Đáp án: B
Phương pháp giải:
Đặt x+1=t. Đưa về tích phân biến t.
\(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( t \right)dt} \)
Lời giải chi tiết:
Đặt x+1=t.
\(\int_0^2 f (x + 1)dx = \int_1^3 {f\left( t \right)dt} \)\( = \int_1^2 f (x)dx - \int_3^2 f (x)dx = 2 - 5 = - 3\)
Câu hỏi 28 :
Kí hiệu \({z_0}\) là nghiệm phức có phần ảo âm của phương trình \(2{z^2} - 6z + 5 = 0.\) Hỏi điểm nào dưới đây là điểm biểu diễn của số phức \(i{z_0}\) ?
- A \({M_2}\left( {\frac{3}{2};\frac{1}{2}} \right)\).
- B \({M_4}\left( { - \frac{1}{2};\frac{3}{2}} \right)\)
- C \({M_3}\left( {\frac{3}{2}; - \frac{1}{2}} \right)\).
- D \({M_1}\left( {\frac{1}{2};\frac{3}{2}} \right)\).
Đáp án: D
Phương pháp giải:
Sử dụng MTCT, Mode 5 -> 3. Bấm hệ số vào tìm nghiệm.
Tính \(i{z_0}\)
Điểm biểu diễn số phức \(z = a + bi\) là: \(M\left( {a;b} \right)\)
Lời giải chi tiết:
\(\begin{array}{l}2{z^2} - 6z + 5 = 0. \Leftrightarrow \left[ \begin{array}{l}z = \frac{3}{2} + \frac{1}{2}\\z = \frac{3}{2} - \frac{1}{2}i\end{array} \right.\\ \Rightarrow {z_0} = \frac{3}{2} - \frac{1}{2}i \Rightarrow i.{z_0} = \frac{1}{2} + \frac{3}{2}i\\ \Rightarrow M\left( {\frac{1}{2};\frac{3}{2}} \right)\end{array}\)
Câu hỏi 29 :
Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành (phần tô đậm) trong hình dưới bằng
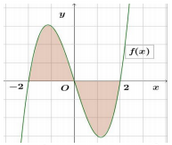
- A \(\int\limits_{ - 2}^0 {f\left( x \right)dx} - \int\limits_0^2 {f\left( x \right)dx} \)
- B \(\int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} \)
- C \(\int\limits_{ - 2}^2 {f\left( x \right)dx} \)
- D \(\int\limits_0^{ - 2} {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} \)
Đáp án: A
Phương pháp giải:
Phần diện tích trên Ox: \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} = \int\limits_a^b {f\left( x \right)dx} \)
Dưới Ox: \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} = - \int\limits_a^b {f\left( x \right)dx} \)
Lời giải chi tiết:
Diện tích phần tô đậm:
\(\begin{array}{l}S = \int\limits_{ - 2}^2 {\left| {f\left( x \right)} \right|dx} \\ = \int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^2 {\left| {f\left( x \right)} \right|dx} \\ = \int\limits_{ - 2}^0 {f\left( x \right)dx} - \int\limits_0^2 {f\left( x \right)dx} \end{array}\)
Câu hỏi 30 :
Cho hai số phức \({z_1} = 2 + i,{z_2} = 2 - i\). Tính \({z_1} - {z_2}\).
- A 4
- B -4
- C -2i
- D 2i
Đáp án: D
Phương pháp giải:
\(\left( {a + bi} \right) \pm \left( {c + di} \right)\)\( = \left( {a \pm c} \right) + \left( {b \pm d} \right)i\)
Lời giải chi tiết:
\({z_1} - {z_2} = \left( {2 + i} \right) - \left( {2 - i} \right) = 2i\)
Câu hỏi 31 :
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;2} \right),B\left( {3;0;2} \right)\). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
- A \(x - y - z + 1 = 0\)
- B \(x - y - 1 = 0\)
- C \(x + y - z - 1 = 0\)
- D \(x + y - 3 = 0\)
Đáp án: B
Phương pháp giải:
Mặt phẳng trung trực của AB là mặt phẳng qua trung điểm I của AB và vuông góc với AB.
Lời giải chi tiết:
Gọi I là trung điểm của AB.
=>\(I\left( {2;1;2} \right)\)
\(\overrightarrow {AB} = \left( {2; - 2;0} \right)\)
Mặt phẳng trung trực của AB: \(1.\left( {x - 2} \right) - 1.\left( {y - 1} \right) = 0\)\( \Leftrightarrow x - y - 1 = 0\)
Câu hỏi 32 :
Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x) = \frac{1}{{x - 1}}\) và \(F(2) = 1\) thì \(F(3)\) bằng
- A \(F(3) = \frac{1}{2}\).
- B \(F(3) = \ln 2\).
- C \(F(3) = \ln 2 + 1\).
- D \(F(3) = \ln \frac{3}{2}\).
Đáp án: C
Phương pháp giải:
Tìm họ nguyên hàm của f(x).
Thay x=2 vào tìm hằng số C.
Lời giải chi tiết:
\(\begin{array}{l}F(x) = \int {\frac{1}{{x - 1}}dx} = \ln \left| {x - 1} \right| + C\\F\left( 2 \right) = 1 \Rightarrow \ln \left| {2 - 1} \right| + C = 1 \Rightarrow C = 1\\ \Rightarrow F\left( 3 \right) = \ln 2 + 1\end{array}\)
Câu hỏi 33 :
Biết \(\int_0^{\frac{\pi }{2}} {(x - 1)} \cos xdx = \frac{{\pi - a}}{b},\left( {a,b \in {\mathbb{N}^*}} \right)\). Tính \({a^2} + 2b\).
- A 18 .
- B 6 .
- C 20 .
- D 8 .
Đáp án: C
Phương pháp giải:
Sử dụng phương pháp tích phân từng phần. Đặt:
\(\begin{array}{l}u = x - 1,dv = \cos xdx\\\int\limits_a^b {udv} = \left. {\left( {uv} \right)} \right|_a^b - \int\limits_a^b {vdu} \end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\int_0^{\frac{\pi }{2}} {(x - 1)} \cos xdx = \int\limits_0^{\frac{\pi }{2}} {\left( {x - 1} \right)d\left( {\sin x} \right)} \\ = \left. {\left[ {\left( {x - 1} \right)\sin x} \right]} \right|_0^{\frac{\pi }{2}} - \int\limits_0^{\frac{\pi }{2}} {\sin xdx} \\ = \frac{\pi }{2} - 1 - 1 = \frac{{\pi - 4}}{2} \Rightarrow a = 4,b = 2\\ \Rightarrow {a^2} + b = 20\end{array}\)
Câu hỏi 34 :
Tìm số phức nghịch đảo của số phức \(z = ai\).
- A \(\frac{1}{a}i\).
- B \(\frac{1}{a}\).
- C \( - ai\).
- D \( - \frac{1}{a}i\)
Đáp án: D
Phương pháp giải:
\(\frac{1}{z} = \frac{{\overline z }}{{{{\left| z \right|}^2}}}\)
Lời giải chi tiết:
\(\frac{1}{z} = \frac{1}{{ai}} = \frac{{ - ai}}{{{a^2}}} = - \frac{1}{a}i\)
Câu hỏi 35 :
Trong không gian với hệ trục toạ độ Oxyz, tính khoảng cách từ điểm \(M(1;2; - 3)\) đến măt phẳng \((P):x + 2y - 2z - 2 = 0\).
- A \(d(M,(P)) = 1\).
- B \(d(M,(P)) = \frac{1}{3}\).
- C \(d(M,(P)) = 3\).
- D \(d(M,(P)) = \frac{{11}}{3}\).
Đáp án: C
Phương pháp giải:
Khoảng cách từ điểm M đến mặt phẳng (P):
\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lời giải chi tiết:
\(\begin{array}{l}d\left( {M,\left( P \right)} \right)\\ = \frac{{\left| {1.1 + 2.2 - 2.\left( { - 3} \right) - 2} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }}\\ = 3\end{array}\)
Câu hỏi 36 :
Tìm \(\int x \ln (x - 1) \cdot dx\).
Phương pháp giải:
Sử dụng phương pháp nguyên hàm từng phần.
Đặt \(u = \ln \left( {x - 1} \right),dv = xdx\)
Lời giải chi tiết:
\(\begin{array}{l}\int x \ln (x - 1) \cdot dx\\ = \frac{1}{2}\int {\ln \left( {x - 1} \right)d\left( {{x^2}} \right)} \\ = \frac{1}{2}{x^2}\ln \left( {x - 1} \right) - \frac{1}{2}\int {\frac{{{x^2}}}{{x - 1}}dx} \\ = \frac{1}{2}{x^2}\ln \left( {x - 1} \right) - \frac{1}{2}\int {\left( {x + 1 + \frac{1}{{x - 1}}} \right)dx} \\ = \frac{1}{2}{x^2}\ln \left( {x - 1} \right) - \frac{{{x^2}}}{4} - \frac{1}{2}x - \frac{1}{2}\ln \left( {x - 1} \right) + C\end{array}\)
Câu hỏi 37 :
Trong không gian Oxyz, viết phương trình của mặt phẳng \((\beta )\) vuông góc với mặt phẳng \((\alpha ):2x - 3y + z - 2 = 0\) đồng thời chứa đường thẳng \(d:\frac{x}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 2}}{{ - 1}}\).
Phương pháp giải:
Tìm vtcp của d và vtpt của \((\alpha )\)
\((\beta )\) vuông góc với \((\alpha )\) và chứa d thì có vtpt vuông góc với vtcp của d và vtpt của \((\alpha )\).
Tính tích có hướng của 2 vecto này.
Lời giải chi tiết:
\(\overrightarrow {{u_d}} = \left( { - 1;2; - 1} \right),\overrightarrow {{n_{\left( \alpha \right)}}} = \left( {2; - 3;1} \right)\)
\(\left[ {\overrightarrow {{n_{\left( \alpha \right)}}} ,\overrightarrow {{u_d}} } \right] = \left( {1;1;1} \right) = \overrightarrow {{n_{\left( \beta \right)}}} \)
Phương trình \((\beta )\) qua \(A\left( {0; - 1;2} \right)\) là: \(x + y + 1 + z - 2 = 0\)\( \Leftrightarrow x + y + z - 1 = 0\)
Câu hỏi 38 :
Cho số phức \(z\) thỏa mãn \(|z + 4 + i| + |z - 4 - 3i| = 4\sqrt 5 \). Tìm giá trị lớn nhất của biểu thức \(P = |z + 6 - 4i|\).
Phương pháp giải:
Đưa về bài toán Oxy.
M, A, B, C lần lượt là điểm biểu diễn \(z,{z_1} = - 4 - i,{z_2} = 4 + 3i,\)\({z_0} = - 6 + 4i\).
Lời giải chi tiết:
Gọi M, A, B, C lần lượt là điểm biểu diễn \(z,{z_1} = - 4 - i,{z_2} = 4 + 3i,\)\({z_0} = - 6 + 4i\).
Khi đó ta có \(AB = \left| {{z_2} - {z_1}} \right| = 4\sqrt 5 \)
\(\begin{array}{l}MA = |z + 4 + i|,MB = |z - 4 - 3i|\\ \Rightarrow MA + MB = AB\end{array}\)
\(CA = \left| {{z_1} - {z_0}} \right| = \sqrt {29} ,\)\(CB = \left| {{z_2} - {z_0}} \right| = \sqrt {101} \)
Do đó M là điểm thuộc đoạn thẳng AB.
\(P = M{C_{\max }}\)\( \Leftrightarrow MC = \max \left\{ {CA,CB} \right\} = CB\)\( = \sqrt {101} \)
Câu hỏi 39 :
Để trang trí cho một căn phòng trong ngôi nhà, ông An vẽ lên tường một hình như sau: trên mỗi cạnh của hình lục giác đều có cạnh bằng 4dm có một cánh hoa hình Parabol, đỉnh của Parabol cách cạnh 5dm và nẳm phía ngoài hình lục giác như hình vẽ dưới. Hãy tính diện tích của hình nói trên (kể cả hình lục giác đều) để mua sơn trang trí cho phù hợp.

Phương pháp giải:
Diện tích hình lục giác đều cạnh a: \(S = 6.\frac{{{a^2}.\sqrt 3 }}{4}\)
Tính diện tích 1 cánh hoa: Diện tích hình phẳng giới hạn bởi đồ thị (P) và trục Ox.
Lời giải chi tiết:
Diện tích hình lục giác đều cạnh 4 dm : \(S = 6.\frac{{{4^2}.\sqrt 3 }}{4} = 24\sqrt 3 \left( {d{m^2}} \right)\)
Gắn trục tọa độ Oxy cho cánh hoa:
Diện tích 1 cánh hoa là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = a{x^2} + bx + c\)

Từ đồ thị ta có \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 0\\c = 5\\4a + 2b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\c = 5\\a = - \frac{5}{4}\end{array} \right.\)\( \Rightarrow y = - \frac{5}{4}{x^2} + 5\).
Diện tích hình phẳng giới hạn bởi đồ thị trên và Ox là: \({S_{1ch}} = \int\limits_{ - 2}^2 {\left| { - \frac{5}{4}{x^2} + 5} \right|dx} = \frac{{40}}{3}\left( {d{m^2}} \right)\)
Vậy diện tích của hình cần tìm là: \(S = 24\sqrt 3 + 80\left( {d{m^2}} \right)\)
Luyện Bài tập trắc nghiệm môn Toán lớp 12 - Xem ngay
Giải chi tiết đề thi học kì 2 môn 12 năm 2020 - 2021 trường THPT Lý Thường Kiệt với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn 12 năm 2020 - 2021 trường THCS-THPT Long Thạnh với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn 12 năm 2020 - 2021 trường THPT Lê Quý Đôn với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn 12 năm 2020 - 2021 trường THPT Đan Phượng với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 trường THPT Yên Lạc 2 - Vĩnh Phúc với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 Sở GD&ĐT Đà Nẵng với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 trường THPT Lý Thái Tổ Bắc Ninh với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 trường THCS & THPT Nguyễn Tất Thành với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 trường THPT chuyên Thái Nguyên với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 12 năm 2019 - 2020 trường THPT Yên Phong 2 - Bắc Ninh với cách giải nhanh và chú ý quan trọng
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |









