Đề kiểm tra 15 phút - Đề số 3 - Chương I - Giải Tích 12

Đề bài

Câu 1. Đồ thị sau đây là của hàm số nào?

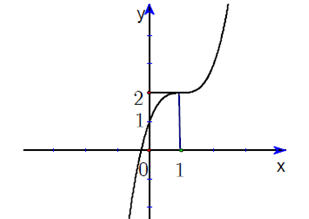
A. \(y =  - {x^3} + 3{x^2} + 1\)

B. \(y = {x^3} - 3x + 1\)

C. \(y = {x^3} - 3{x^2} + 3x + 1\)

D. \(y =  - {x^3} - 3{x^2} - 1\)

Câu 2. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sau đây ?

A. \(y = \dfrac{{2x - 2}}{{x + 2}}\)

B. \(y = \dfrac{{{x^2} + 2x + 2}}{{1 + x}}\)

C. \(y = \dfrac{{2{x^2} + 3}}{{2 - x}}\)

D. \(y = \dfrac{{1 + x}}{{1 - 2x}}\)

Câu 3. Hàm số \(y =  - {x^3} + 3{x^2} - 1\) đồng biến trên khoảng nào ?

A. \(( - \infty ;1)\)

B. \((0;2)\)

C. \((2; + \infty )\)

D. \(( - \infty ; + \infty )\)

Câu 4. Tìm giá trị lớn nhất của hàm số \(y = \sqrt { - {x^2} + 4x} \).

A. 0                    B. 4

C. – 2                 D. 2.

Câu 5. Số giao điểm của đồ thị hàm số \(y = {x^4} + {x^2} - 2\) với trục hoành là

A. 0                    B. 3

C. 2                    D. 1

Câu 6. Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) với a > 0 có đồ thị như hình vẽ sau. Mệnh đề nào đúng ?

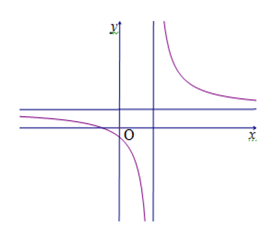
A. b < 0, c < 0, d < 0.

B. b > 0 , c > 0, d < 0.

C. b < 0, c > 0, d < 0.

D. b > 0, c < 0, d < 0.

Câu 7. Trong những điểm sau điểm nào thuộc đồ thị hàm số \(y = \dfrac{{x + 1}}{{2x - 1}}\) ?

A. (2 ; - 1)                    B. (1 ; 2)

C. (1; 0)                        D. (0 ; 1).

Câu 8. Đồ thị sau đây là của hàm số nào?

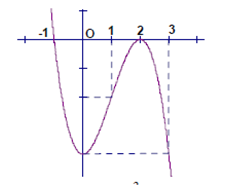
A. \(y = {x^3} + 3x - 4\)

B. \(y =  - {x^3} + 3{x^2} - 4\)

C. \(y = {x^3} - 3x - 4\)

D.. \(y = {x^3} - 3{x^2} - 4\)

Câu 9. Cho hàm số y=f(x) xác định và lien tục trên khoảng \(( - \infty ; + \infty )\) có bảng biến thiên như sau:

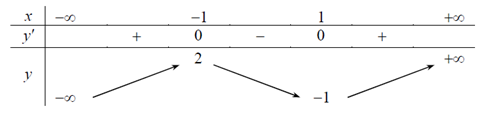
Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng \((1; + \infty )\).

B. Hàm số đồng biến trên khoảng \(( - \infty ; - 2)\).

C. Hàm số nghịch biến trên khoảng \(( - \infty ;1)\).

D. Hàm số đồng biến trên khoảng \(( - 1; + \infty )\).

Câu 10. Tìm số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{{x^2} - 5x + 4}}{{{x^2} - 1}}\)

A.  0                             B. 2

C.  1                             D. 3

Lời giải chi tiết

Câu 1. 

Đồ thị hàm số đi lên nên loại A, D.

Hàm số đồng biến trên R nên \(y' \ge 0,\forall x \in R\).

Do câu C có \(y' = 3{x^2} - 6x + 3 = 0\)

\( = 3\left( {{x^2} - 2x + 1} \right)\) \( = 3{\left( {x - 1} \right)^2} \ge 0,\forall x \in R\)

\( \Leftrightarrow \) hàm số ở đáp án C thỏa mãn.

Chọn C.

Câu 2.

Do \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{{2x - 2}}{{x + 2}} \)\(= \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{2x - 2}}{{x + 2}} = 2\)

Chọn A.

Câu 3.

Ta có \(y' =  - 3{x^2} + 6x,\,\,y' = 0\)

\(\Rightarrow \,\, - 3{x^2} + 6x = 0\)

\(\Leftrightarrow \,\,\left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)

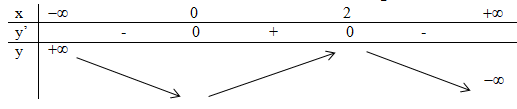
Vậy hàm số đồng biến trên \(\left( {0;2} \right)\)

Chọn B. 

Câu 4.

Ta có \(D = [0;4],\)

\(y' = \dfrac{{ - 2x + 4}}{{2\sqrt { - {x^2} + 4x} }} = 0 \Rightarrow \,\,x = 2\).

\(y(0) = 0, y( 2) = 2, y(4) = 0.\)

Vậy giá trị lớn nhất của hàm số là 2.

Chọn D.

Câu 5.

Số giao điểm của đồ thị hàm số \(y = {x^4} + {x^2} - 2\) với trục hoành là số nghiệm của phương trình \({x^4} + {x^2} - 2 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}
{x^2} = 1\\
{x^2} = - 2\left( {VN} \right)
\end{array} \right.\)

\( \Leftrightarrow \,\,\left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\).

Vậy số giao điểm là 2.

Chọn C.

Câu 6. Do đường tiệm cận ngang nằm phía trên trục hoành mà \(a > 0\) nên \(\frac{a}{c} > 0 \Rightarrow c > 0\)

Do đường tiệm cận đứng nằm bên phải trục tung nên \( - \frac{d}{c} > 0\), mà \(c > 0\) suy ra \(d <  0.\)

Đồ thị hàm số cắt trục Oy tại điểm \(\left( {0;\frac{b}{d}} \right)\).

Từ đồ thị suy ra \(\frac{b}{d} < 0 \Rightarrow b > 0\) (do d < 0)

Chọn  B.

Câu 7.

Thay tọa độ điểm vào hàm số ta có  điểm \((1; 2)\) thuộc đồ thị hàm số.

Chọn B.

Câu 8.

Nhìn vào đồ thị hàm số ta có \(a < 0\) nên loại A, C, D.

Chọn B.

Câu 9.

Từ bảng biến thiên suy ra hàm số đồng biến trên khoảng \((1; + \infty )\) và \(( - \infty ; - 1)\).

Mà \(\left( { - \infty ; - 2} \right) \subset \left( { - \infty ; - 1} \right)\) nên hàm số đồng biến trên \(\left( { - \infty ; - 2} \right) \).

Chọn B.

Câu 10.

\(\mathop {\lim }\limits_{x \to  \pm \infty } \frac{{{x^2} - 5x + 4}}{{{x^2} - 1}} = 1\) nên \(y = 1\) là đường TCN của đồ thị hàm số.

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 5x + 4}}{{{x^2} - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x - 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{x - 4}}{{x + 1}} =  - \frac{3}{2}\end{array}\)

Nên \(x = 1\) không là TCĐ của đồ thị hàm số.

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  - {1^ + }} \frac{{{x^2} - 5x + 4}}{{{x^2} - 1}}\\ = \mathop {\lim }\limits_{x \to  - {1^ + }} \frac{{\left( {x - 1} \right)\left( {x - 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to  - {1^ + }} \frac{{x - 4}}{{x + 1}} =  - \infty \\\mathop {\lim }\limits_{x \to  - {1^ - }} \frac{{{x^2} - 5x + 4}}{{{x^2} - 1}} =  + \infty \end{array}\)

Nên \(x =  - 1\) là đường TCĐ của đồ thị hàm số.

Chú ý:

Có thể nhận xét nhanh x=1 là nghiệm của mẫu và cũng là nghiệm của tử (cùng bậc) nên x=1 không là TCĐ.

Còn x=-1 là nghiệm của mẫu nhưng không là nghiệm của tử nên x=-1 là đường TCĐ.

Chọn B.

Loigiaihay.com