Trắc nghiệm Bài 35: Định lí Pythagore và ứng dụng Toán 8 Kết nối tri thức
Đề bài
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
-
A.
6 cm
-
B.
8 cm
-
C.
9 cm
-
D.
12 cm
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
-
A.
\(B{{{D}}^2} - B{C^2} = C{{D}}{{.AB}}\)
-
B.
\(B{{{D}}^2} - B{C^2} = A{B^2}\)
-
C.
\(B{{{D}}^2} - B{C^2} = 2C{{D}}.AB\)
-
D.
\(B{{{D}}^2} - B{C^2} = BC.AB\)
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
-
A.
\(7\;cm\).
-
B.
\(13\;cm\).
-
C.
\(15\;cm\).
-
D.
\(17\;cm\).
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
-
A.
\(7\;cm\).
-
B.
\(8\;cm\).
-
C.
\(9\;cm\).
-
D.
\(10\;cm\).
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
-
A.
10cm
-
B.
9cm
-
C.
5cm
-
D.
8cm
Chọn phát biểu đúng nhất về định lí Pythagore:
-
A.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
-
B.
Trong một tam giác vuông, cạnh huyền bằng cạnh góc vuông.
-
C.
Trong tam giác vuông, bình phương cạnh huyền bằng bình phương cạnh góc vuông.
-
D.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng hai cạnh góc vuông.
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
-
A.
BC = 4 dm.
-
B.
\(BC = \sqrt {64} dm\).
-
C.
BC = 8 dm.
-
D.
\(BC = \sqrt 8 dm\)
-
A.
x = 10 cm.
-
B.
x = 11 cm.
-
C.
x = 8 cm.
-
D.
x = 5 cm
Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
-
A.
12cm ; 24cm.
-
B.
10cm ; 22 cm.
-
C.
10cm ; 24cm.
-
D.
15cm ; 24cm.
-
A.
\(5\).
-
B.
\(5\sqrt 4 \).
-
C.
\(4\).
-
D.
\(4\sqrt 5 \).
Lựa chọn phương án đúng nhất:
-
A.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác nhọn.
-
B.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
-
C.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác tù.
-
D.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác cân.
Cho tam giác ABC vuông tại B, khi đó:
-
A.
\(A{B^2} + B{C^2} = A{C^2}\)
-
B.
\(A{B^2} - B{C^2} = A{C^2}\)
-
C.
\(A{B^2} + A{C^2} = B{C^2}\).
-
D.
\(A{B^2} = A{C^2} + B{C^2}\)
Tam giác ABC có AB = 3 cm, AC = 4cm, BC = 5cm. Tam giác ABC là tam giác gì?
-
A.
Tam giác nhọn
-
B.
Tam giác tù.
-
C.
Tam giác vuông.
-
D.
Không đủ dữ kiện để xác định
Cạnh huyền của một tam giác là bao nhiêu biết hai cạnh góc vuông là 3 và 4.
-
A.
8
-
B.
7
-
C.
6
-
D.
5
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm, AB = 4cm. Tính AH:
-
A.
\(\sqrt {10} cm\).
-
B.
\(\sqrt {13} cm\).
-
C.
\(\sqrt {12} cm\).
-
D.
12 cm.
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
15cm; 8cm; 18cm.
-
B.
21dm; 20dm; 29dm.
-
C.
5m; 6m; 8m.
-
D.
2m; 3m; 4m.
-
A.
\(AC = 4\sqrt 2 cm\).
-
B.
\(AC = 4cm\).
-
C.
\(AC = \sqrt {30} cm\).
-
D.
\(AC = 8cm\).
Tìm câu sai trong các câu sau đây. Cho tam giác PQR vuông tại P. Khi đó:
-
A.
QR > PQ
-
B.
QR > PR
-
C.
\(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\)
-
D.
\(Q{{{R}}^2} + P{{{R}}^2} = P{Q^2}\)
Cho tam giác ABC vuông ở A có AC = 20 cm. Kẻ \(AH \bot BC\). Biết BH = 9cm; HC = 16cm. Tính AB , AH
-
A.
AH = 12cm; AB = 15cm.
-
B.
AH = 10cm; AB = 15 cm.
-
C.
AH = 15cm; AB = 12cm.
-
D.
AH = 12cm; AB = 13 cm.
Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4 cm, \(HC = \sqrt {184} cm\). (làm tròn đến chữ số thập phân thứ nhất).
-
A.
30,8cm.
-
B.
35, 7cm.
-
C.
31 cm.
-
D.
31, 7cm.
Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4 và chu vi tam giác là 36 cm
-
A.
9cm.
-
B.
12cm .
-
C.
15cm.
-
D.
16cm.
-
A.
x = 6
-
B.
x = 7
-
C.
x = 8
-
D.
x = 5
-
A.
x = 2
-
B.
x = 1,5
-
C.
x = 1
-
D.
x = 1,2
-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
Cho tam giác ABC biết BC = 7,5cm; CA = 4,5cm, AB = 6cm. Độ dài đường cao AH của tam giác ABC là:
-
A.
12,96cm
-
B.
6,48cm
-
C.
3,6cm
-
D.
6,3cm
Cho tam giác ABC cân tại A biết AB = AC = 17cm. Kẻ \(B{\rm{D}} \bot AC\), biết BD = 15cm. Tính cạnh đáy BC.
-
A.
17 cm
-
B.
16 cm
-
C.
\(3\sqrt {14} \)cm
-
D.
\(3\sqrt {34} cm\)
-
A.
36
-
B.
40
-
C.
42
-
D.
30
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm ; BH = 4,5cm và HC = 8cm. Khi đó tam giác ABC là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Một tam giác có độ dài ba đường cao là 4,8cm ; 6cm ; 8cm. Tam giác đó là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Lời giải và đáp án
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
Đáp án : B
Sử dụng định lí Pytago trong tam giác vuông.
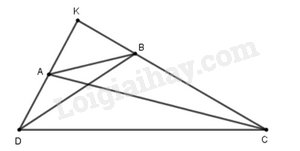
Gọi K là giao điểm AD, BC.
Vì \(\widehat C + \widehat D = {90^o}\) nên \(\widehat K = {90^o}\)
Áp dụng định lí Pytago trong tam giác vuông vào các tam giác:
+ ΔKAC vuông tại K ta có: AC2 = KC2 + KA2.
+ ΔKBD vuông tại K ta có: BD2 = KB2 + KD2.
+ ΔKBA vuông tại K ta có: BA2 = KA2 + KB2.
+ ΔKBD vuông tại K ta có: CD2 = KC2 + KD2.
Từ đó AC2+ BD2 = KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2) = AB2 + DC2.
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
-
A.
6 cm
-
B.
8 cm
-
C.
9 cm
-
D.
12 cm
Đáp án : D
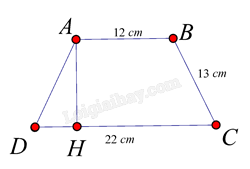
Xét hình thang cân ABCD có đáy lớn CD và đáy nhỏ AB đường cao AH ta có:
\(C{{D}} = AB + 2.DH \Rightarrow DH = \frac{{C{{D}} - AB}}{2} \Rightarrow DH = \frac{{22 - 12}}{2} = 5cm\)
Áp dụng định lí Pythago cho tam giác AHD vuông tại H có AD = BC = 13 cm và
DH = 5 cm ta có:
\(A{H^2} = A{{{D}}^2} - D{H^2} = {13^2} - {5^2} = 144 \Rightarrow AH = \sqrt {144} = 12cm\)
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
-
A.
\(B{{{D}}^2} - B{C^2} = C{{D}}{{.AB}}\)
-
B.
\(B{{{D}}^2} - B{C^2} = A{B^2}\)
-
C.
\(B{{{D}}^2} - B{C^2} = 2C{{D}}.AB\)
-
D.
\(B{{{D}}^2} - B{C^2} = BC.AB\)
Đáp án : A
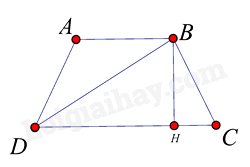
Kẻ \(BH \bot C{{D}}\) tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có: \(B{{{D}}^2} = D{H^2} + B{H^2}\)
Xét tam giác vuông CBH, theo định lý Pytago ta có: \(B{C^2} = C{H^2} + B{H^2}\)
Suy ra: \(B{{{D}}^2} - B{C^2} = D{H^2} - C{H^2} = \left( {DH + CH} \right)\left( {DH - CH} \right) = C{{D}}.AB\)
(Do DH + CH = CD; DH – CH = AB)
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
-
A.
\(7\;cm\).
-
B.
\(13\;cm\).
-
C.
\(15\;cm\).
-
D.
\(17\;cm\).
Đáp án : B
Áp dụng định lý Pytago trong tam giác vuông, ta được độ dài đường chéo hình chữ nhật bằng
\(\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\;\left( {cm} \right)\)
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
-
A.
\(7\;cm\).
-
B.
\(8\;cm\).
-
C.
\(9\;cm\).
-
D.
\(10\;cm\).
Đáp án : B
Hình chữ nhật \(ABCD\) có \(CD = AB = 6\;\;cm\).
Áp dụng định lý Pytago trong tam giác \(BCD\) , ta có:
\(BC = \sqrt {B{D^2} - C{D^2}} = \sqrt {{{10}^2} - {6^2}} = \sqrt {64} = 8\;\;\left( {cm} \right)\)
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
-
A.
10cm
-
B.
9cm
-
C.
5cm
-
D.
8cm
Đáp án : C
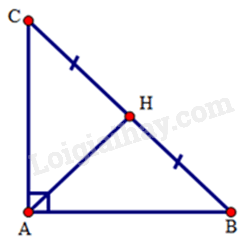
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 62 + 82
⇒ BC2 = 100. Suy ra BC = 10 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 10 : 2 = 5cm
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Chọn phát biểu đúng nhất về định lí Pythagore:
-
A.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
-
B.
Trong một tam giác vuông, cạnh huyền bằng cạnh góc vuông.
-
C.
Trong tam giác vuông, bình phương cạnh huyền bằng bình phương cạnh góc vuông.
-
D.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng hai cạnh góc vuông.
Đáp án : A
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
-
A.
BC = 4 dm.
-
B.
\(BC = \sqrt {64} dm\).
-
C.
BC = 8 dm.
-
D.
\(BC = \sqrt 8 dm\)
Đáp án : D
Tam giác ABC vuông cân ở A nên theo định lý Pythagore ta có \(A{B^2} + A{C^2} = B{C^2}\) mà
AB = AC = 2 dm
Nên \(B{C^2} = {2^2} + {2^2} = 8 \Rightarrow BC = \sqrt 8 dm\)
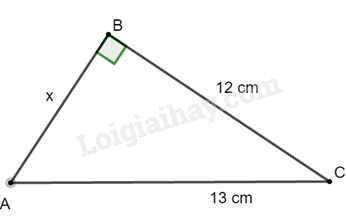
-
A.
x = 10 cm.
-
B.
x = 11 cm.
-
C.
x = 8 cm.
-
D.
x = 5 cm
Đáp án : D
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta được :
\(A{C^2} = A{B^2} + B{C^2} \)
\(A{B^2} = A{C^2} - B{C^2} \)
\({x^2} = {13^2} - {12^2} = 25 \)
\(x = 5cm\)
Vậy x = 5 cm
Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
-
A.
12cm ; 24cm.
-
B.
10cm ; 22 cm.
-
C.
10cm ; 24cm.
-
D.
15cm ; 24cm.
Đáp án : C
Gọi độ dài hai cạnh góc vuông là \(x,y\left( {x,y > 0} \right)\)
Theo định lý Pytago ta có: \({x^2} + {y^2} = 26{}^2 \Rightarrow {x^2} + {y^2} = 676\)
Theo đề bài ta có: \(\frac{x}{5} = \frac{y}{{12}} \Rightarrow \frac{{{x^2}}}{{25}} = \frac{{{y^2}}}{{144}} = \frac{{{x^2} + {y^2}}}{{25 + 144}} = \frac{{676}}{{169}} = 4\)
Suy ra \({x^2} = 25.4 \Rightarrow {x^2} = 100 \Rightarrow x = 10cm\)
\({y^2} = 144.4 \Rightarrow {y^2} = 576 \Rightarrow y = 24cm\)
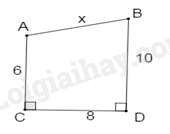
-
A.
\(5\).
-
B.
\(5\sqrt 4 \).
-
C.
\(4\).
-
D.
\(4\sqrt 5 \).
Đáp án : D
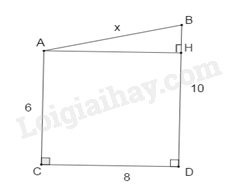
Kẻ \(AH \bot B{{D}}\) tại H.
Khi đó ACDH là hình chữ nhật, suy ra: HD = AC = 6; AH = CD = 8.
Do đó: BH = BD – HD = 10 – 6 = 4
Áp dụng định lí Pythagore cho tam giác AHB vuông tại H, ta có:
\(A{B^2} = B{H^2} + A{H^2} = {4^2} + {8^2} = 80\)
suy ra \(AB = 4\sqrt 5 \)
Vậy \(x = 4\sqrt 5 \)
Lựa chọn phương án đúng nhất:
-
A.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác nhọn.
-
B.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
-
C.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác tù.
-
D.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác cân.
Đáp án : B
Cho tam giác ABC vuông tại B, khi đó:
-
A.
\(A{B^2} + B{C^2} = A{C^2}\)
-
B.
\(A{B^2} - B{C^2} = A{C^2}\)
-
C.
\(A{B^2} + A{C^2} = B{C^2}\).
-
D.
\(A{B^2} = A{C^2} + B{C^2}\)
Đáp án : A
Vì tam giác ABC vuông tại B nên theo định lý Pythagore ta có \(A{B^2} + B{C^2} = A{C^2}\).
Tam giác ABC có AB = 3 cm, AC = 4cm, BC = 5cm. Tam giác ABC là tam giác gì?
-
A.
Tam giác nhọn
-
B.
Tam giác tù.
-
C.
Tam giác vuông.
-
D.
Không đủ dữ kiện để xác định
Đáp án : C
\(\begin{array}{l}A{B^2} + A{C^2} = {3^2} + {4^2} = 25\\B{C^2} = {5^2} = 25\\ \Rightarrow A{B^2} + A{C^2} = B{C^2}\end{array}\)
Vậy tam giác ABC là tam giác vuông
Cạnh huyền của một tam giác là bao nhiêu biết hai cạnh góc vuông là 3 và 4.
-
A.
8
-
B.
7
-
C.
6
-
D.
5
Đáp án : D
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm, AB = 4cm. Tính AH:
-
A.
\(\sqrt {10} cm\).
-
B.
\(\sqrt {13} cm\).
-
C.
\(\sqrt {12} cm\).
-
D.
12 cm.
Đáp án : C
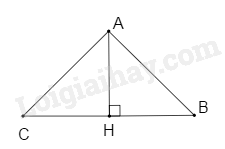
Áp dụng định lí Pythagore cho \(\Delta ABH\) vuông tại H ta có:
\(A{B^2} = B{H^2} + A{H^2} \)
suy ra \(A{H^2} = A{B^2} - B{H^2} = {4^2} - {2^2} = 12\)
nên \(AH = \sqrt {12} cm\)
Vậy \(AH = \sqrt {12} cm\)
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
15cm; 8cm; 18cm.
-
B.
21dm; 20dm; 29dm.
-
C.
5m; 6m; 8m.
-
D.
2m; 3m; 4m.
Đáp án : B
+) Với bộ số: 15cm; 8cm; 18cm ta thấy : \({18^2} = 324{,^{}}{15^2} + {8^2} = 289 < 324\) nên loại đáp án A.
+) Với bộ số: 21dm; 20dm; 29dm ta thấy : \({29^2} = 841{;^{}}{21^2} + {20^2} = 841 = {29^2}\) nên đây là ba cạnh của tam giác vuông.
+) Với bộ số: 5m; 6m; 8m ta thấy : \({8^2} = 64{;^{}}{5^2} + {6^2} = 61 < 64\) nên loại đáp án C.
+) Với bộ số: 2m; 3m; 4m ta thấy : \({4^2} = 16{;^{}}{3^2} + {2^2} = 13 < 16\) nên loại đáp án D.
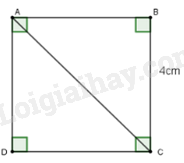
-
A.
\(AC = 4\sqrt 2 cm\).
-
B.
\(AC = 4cm\).
-
C.
\(AC = \sqrt {30} cm\).
-
D.
\(AC = 8cm\).
Đáp án : A
Vì ABCD là hình vuông nên AB = AC = 4cm
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. cho tam giác ABC vuông tại B ta có
\(A{C^2} = A{B^2} + B{C^2} = {4^2} + {4^2} = 32 \Rightarrow AC = \sqrt {32} = 4\sqrt 2 cm\)
Tìm câu sai trong các câu sau đây. Cho tam giác PQR vuông tại P. Khi đó:
-
A.
QR > PQ
-
B.
QR > PR
-
C.
\(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\)
-
D.
\(Q{{{R}}^2} + P{{{R}}^2} = P{Q^2}\)
Đáp án : D
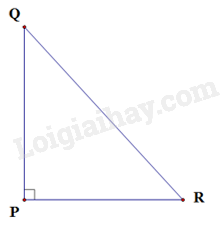
Tam giác PQR vuông tại P nên theo định lí Pythagore ta có: \(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\) nên câu C đúng.
Vì độ dài đoạn thẳng là một số dương nên QR > PQ; QR > PR
Suy ra các câu A, B đúng.
Câu trả lời sai là câu D.
Cho tam giác ABC vuông ở A có AC = 20 cm. Kẻ \(AH \bot BC\). Biết BH = 9cm; HC = 16cm. Tính AB , AH
-
A.
AH = 12cm; AB = 15cm.
-
B.
AH = 10cm; AB = 15 cm.
-
C.
AH = 15cm; AB = 12cm.
-
D.
AH = 12cm; AB = 13 cm.
Đáp án : A
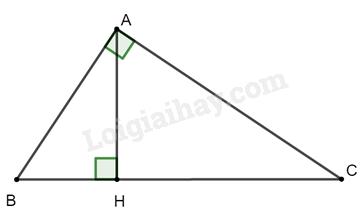
+) Ta có: BC = BH + HC = 9 + 16 = 25 cm
+) Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow A{B^2} = B{C^2} - A{C^2} = {25^2} - {20^2} = 225 \Rightarrow AB = 15cm\)
+) Xét tam giác ABH vuông tại H, theo định lí Pythagore ta có:
\(H{B^2} + H{A^2} = A{B^2} \Rightarrow A{H^2} = A{B^2} - H{B^2} = {15^2} - {9^2} = 144 \Rightarrow AH = 12cm\)
+) Vậy AH = 12cm ; AB = 15cm
Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4 cm, \(HC = \sqrt {184} cm\). (làm tròn đến chữ số thập phân thứ nhất).
-
A.
30,8cm.
-
B.
35, 7cm.
-
C.
31 cm.
-
D.
31, 7cm.
Đáp án : B
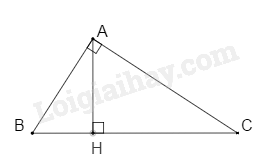
Áp dụng định lí Pythagore cho tam giác ABH vuông tại H, ta có:
\(\begin{array}{l}A{B^2} = B{H^2} + A{H^2} \Rightarrow B{H^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\\ \Rightarrow BH = 3(cm)\end{array}\)
Suy ra: \(BC = HB + HC = 3 + \sqrt {184} \)
Áp dụng định lí Pythagore cho tam giác AHC vuông tại H ta có:
\(A{C^2} = C{H^2} + A{H^2} = {4^2} + {\left( {\sqrt {184} } \right)^2} = 200 \Rightarrow AC = \sqrt {200} \)
Vậy chu vi tam giác ABC là: \(AB + AC + BC = 5 + \sqrt {200} + 3 + \sqrt {184} \approx 35,7cm\)
Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4 và chu vi tam giác là 36 cm
-
A.
9cm.
-
B.
12cm .
-
C.
15cm.
-
D.
16cm.
Đáp án : C
Gọi độ dài hai cạnh góc vuông là \(x,y\left( {y > x > 0} \right)\) (cm) và độ dài cạnh huyền là \(z\left( {z > y} \right)\)(cm)
Theo đề bài ta có \(\frac{x}{3} = \frac{y}{4}\) và x + y + z = 36
Đặt \(\frac{x}{3} = \frac{y}{4} = k\left( {k > 0} \right) \Rightarrow x = 3k;y = 4k\)
Theo định lý Pythagore ta có: \({x^2} + {y^2} = {z^2} \Rightarrow {z^2} = {\left( {3k} \right)^2} + {\left( {4k} \right)^2} = 25{k^2} = {\left( {5k} \right)^2} \Rightarrow z = 5k\)
Suy ra \(x + y + z = 3k + 4k + 5k = 12k = 36 \Rightarrow k = 3\) (thỏa mãn)
Từ đó: \(x{{ }} = {{ }}9{{ }}cm;{{ }}y{{ }} = {{ }}12{{ }}cm;{{ }}z{{ }} = {{ }}15cm.\)
Vậy cạnh huyền dài 15 cm
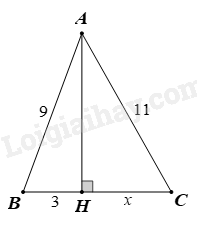
-
A.
x = 6
-
B.
x = 7
-
C.
x = 8
-
D.
x = 5
Đáp án : B
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. vào Tam giác ABH vuông tại H ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow A{H^2} = A{B^2} - B{H^2} = {9^2} - {3^2} = 72\end{array}\)
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. vào tam giác ACH vuông tại H ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow H{C^2} = A{C^2} - A{H^2} = {11^2} - 72 = 49\\ \Rightarrow x = HC = \sqrt {49} = 7\end{array}\)
-
A.
x = 2
-
B.
x = 1,5
-
C.
x = 1
-
D.
x = 1,2
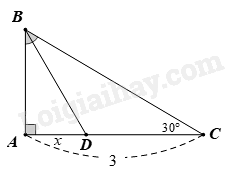
Đáp án : C
Tam giác ABC vuông tại A nên \(\widehat {ABC} + \widehat {ACB} = {90^o} \) nên \(\widehat {ABC} = {90^o} - \widehat {ACB} = {90^o} - {30^o} = {60^o}\).
Lại có BD là tia phân giác của \(\widehat {ABC}\) (gỉa thiết) nên \(\widehat {AB{{D}}} = \widehat {DBC} = \frac{{\widehat {ABC}}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\).
Tam giác ABC vuông tại A có \(\widehat {ACB} = {30^o}\) nên \(AB = \frac{1}{2}BC\) hay BC = 2 AB.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ {\left( {2{{A}}B} \right)^2} = A{B^2} + {3^2}\\ 4{{A}}B = A{B^2} + 9\\ 3{{A}}{B^2} = 9\\ A{B^2} = 3\\ AB = \sqrt 3 \end{array}\)
Tam giác ABC vuông tại A có: \(\widehat {AB{{D}}} = {30^o}\) nên \(A{{D}} = \frac{1}{2}B{{D}}\) hay BD = 2AD.
Áp dụng định lý Pythagore vào tam giác ABD vuông tại A ta có:
\(\begin{array}{l}B{{{D}}^2} = A{B^2} + A{{{D}}^2}\\ {\left( {2{{AD}}} \right)^2} = A{B^2} + A{{{D}}^2}\\ {\left( {2x} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {x^2}\\ 4{{{x}}^2} = 3 + {x^2}\\ 3{{{x}}^2} = 3\\ {x^2} = 1\\ x = 1\end{array}\)
-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
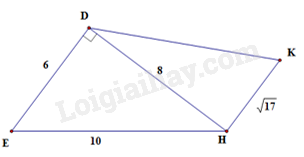
Đáp án : C
Ta có DE // HK nên: \(\widehat {E{{D}}H} = \widehat {DHK} = {90^o}\) (so le trong)
Áp dụng định lí Pythagore trong tam giác vuông DHK ta được:
\(D{K^2} = D{H^2} + H{K^2}\)
\(D{K^2} = {8^2} + {\left( {\sqrt {17} } \right)^2}\)
\(D{K^2} = 64 + 17 = 81 = {9^2}\\DK = 9\)
Cho tam giác ABC biết BC = 7,5cm; CA = 4,5cm, AB = 6cm. Độ dài đường cao AH của tam giác ABC là:
-
A.
12,96cm
-
B.
6,48cm
-
C.
3,6cm
-
D.
6,3cm
Đáp án : C
+ Áp dụng định lí Pythagore trong tam giác vuông.
+ Trong tam giác vuông, tích của hai cạnh góc vuông bằng tích của đường cao nhân với cạnh huyền.
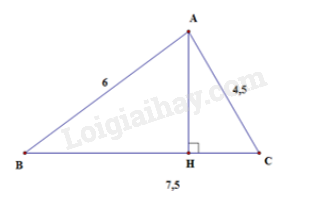
\(B{C^2} = {\left( {7,5} \right)^2} = 56,25\)
\(A{C^2} + A{B^2} = {\left( {4,5} \right)^2} + {6^2} = 56,25\)
Ta thấy: \(B{C^2} = A{B^2} + A{C^2}\)
Suy ra tam giác ABC vuông tại A.
Ta lại có: \(AB.AC = AH.BC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{6.4,5}}{{7,5}} = 3,6(cm)\)
Cho tam giác ABC cân tại A biết AB = AC = 17cm. Kẻ \(B{\rm{D}} \bot AC\), biết BD = 15cm. Tính cạnh đáy BC.
-
A.
17 cm
-
B.
16 cm
-
C.
\(3\sqrt {14} \)cm
-
D.
\(3\sqrt {34} cm\)
Đáp án : D
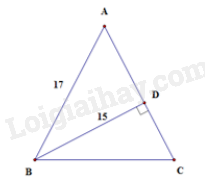
Tam giác ABD vuông tại D nên theo định lí Pythagore ta có: \(A{{\rm{D}}^2} = A{B^2} - B{{\rm{D}}^2} = {17^2} - {15^2} = 64 = {8^2} \)
nên \(A{\rm{D}} = 8(cm)\)
Suy ra \( C{\rm{D}} = AC - A{\rm{D}} = 17 - 8 = 9(cm)\)
Tam giác BCD vuông tại D nên theo định lí Pythagore ta có:
\(\begin{array}{l}B{C^2} = C{{\rm{D}}^2} - B{{\rm{D}}^2} = {9^2} + {15^2} = 81 + 225 = 306\end{array}\)
nên \(BC = 3\sqrt {34} (cm)\)
-
A.
36
-
B.
40
-
C.
42
-
D.
30
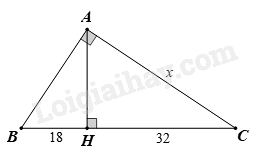
Đáp án : B
Áp dụng định lý Pythagore vào tam giác AHB vuông tại H ta có:
\(A{H^2} + B{H^2} = A{B^2} \Rightarrow A{H^2} = A{B^2} - B{H^2}(1)\)
Áp dụng định lý Pythagore vào tam giác AHC vuông tại H ta có:
\(A{H^2} + C{H^2} = A{C^2} \Rightarrow A{H^2} = A{C^2} - C{H^2} = (2)\)
Từ (1) và (2) ta có: \(A{B^2} - B{H^2} = A{C^2} - C{H^2}\)
\(\begin{array}{l} \Rightarrow A{B^2} - {18^2} = {x^2} - {32^2}\\ \Rightarrow A{B^2} = {x^2} - {32^2} + {18^2}\\ \Rightarrow A{B^2} = {x^2} - 1024 + 324\\ \Rightarrow A{B^2} = {x^2} - 700\end{array}\)
Ta có: BC = BH + CH = 18 + 32 = 50
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{B^2} + {x^2} = {50^2}(3)\end{array}\)
Thay \(A{B^2} = {x^2} - 700\) vào (3) ta được:
\(\begin{array}{l}{x^2} - 700 + {{\rm{x}}^2} = {50^2}\\ \Rightarrow 2{{\rm{x}}^2} = 2500 + 700\\ \Rightarrow 2{{\rm{x}}^2} = 3200\\ \Rightarrow {x^2} = 3200:2 = 1600\\ \Rightarrow x = \sqrt {1600} = 40\end{array}\)
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm ; BH = 4,5cm và HC = 8cm. Khi đó tam giác ABC là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Đáp án : B
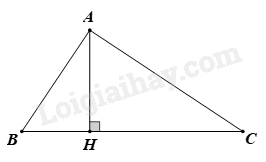
Áp dụng định lý Pythagore vào tam giác AHB vuông tại H ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow AB = {6^2} + 4,{5^2} = 36 + \frac{{81}}{4} = \frac{{225}}{4}\end{array}\)
Áp dụng định lý Pythagore vào tam giác AHC vuông tại H ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow A{C^2} = {6^2} + {8^2} = 100\end{array}\)
Ta có: \(BC = BH + HC = 4,5 + 8 = \frac{{25}}{2}\)
\( \Rightarrow B{C^2} = {\left( {\frac{{25}}{2}} \right)^2} = \frac{{625}}{4}(1)\)
Ta có: \(A{B^2} + A{C^2} = \frac{{225}}{4} + 100 = \frac{{625}}{4}(2)\)
Từ (1) và (2) suy ra: \(B{C^2} = A{B^2} + A{C^2}\)
Vậy tam giác ABC vuông tại A
Một tam giác có độ dài ba đường cao là 4,8cm ; 6cm ; 8cm. Tam giác đó là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Đáp án : B
Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích của tam giác ABC \(\left( {a,b,c,S > 0} \right)\). Chứng minh \({a^2} = {b^2} + {c^2}\) suy ra tam giác ABC là tam giác vuông.
Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích của tam giác ABC \(\left( {a,b,c,S > 0} \right)\)
Ta có: \(S = \frac{1}{2}.4,8.a = \frac{1}{6}.6.b = \frac{1}{2}.8.c\) hay \(4,8{\rm{a}} = 6b = 8c = 2{\rm{S}}\)
Do đó: \(a = \frac{{2{\rm{S}}}}{{4,8}} = \frac{{5{\rm{S}}}}{{12}};b = \frac{{2{\rm{S}}}}{6} = \frac{S}{3};c = \frac{{2{\rm{S}}}}{8} = \frac{S}{4}\)
Ta có: \({b^2} + {c^2} = {\left( {\frac{S}{3}} \right)^2} + {\left( {\frac{S}{4}} \right)^2} = \frac{{{S^2}}}{9} + \frac{{{S^2}}}{{16}} = \frac{{25{{\rm{S}}^2}}}{{144}};{a^2} = {\left( {\frac{{5{\rm{S}}}}{{12}}} \right)^2} = \frac{{25{{\rm{S}}^2}}}{{144}}\)
Suy ra \({a^2} = {b^2} + {c^2}\) nên tam giác đã cho là tam giác vuông, đỉnh góc vuông ứng với đường cao có độ dài là 4,8cm
Luyện tập và củng cố kiến thức Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 37: Hình đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 34: Ba trường hợp đồng dạng của hai tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 33: Hai tam giác đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 39: Hình chóp tứ giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 38: Hình chóp tam giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 37: Hình đồng dạng Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 35: Định lí Pythagore và ứng dụng Toán 8 Kết nối tri thức










Danh sách bình luận