Trắc nghiệm Bài 34: Ba trường hợp đồng dạng của hai tam giác Toán 8 Kết nối tri thức
Đề bài
Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :
-
A.
\(3cm;4cm;6cm\) và \(9cm;15cm;18cm\) .
-
B.
\(4cm;5cm;6cm\) và \(8cm;10cm;12cm\) .
-
C.
\(6cm;5cm;6cm\) và \(3cm;5cm;3cm\) .
-
D.
\(5cm;7cm;1dm\) và \(10cm;14cm;18cm\) .
Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?
-
A.
\(\Delta ABC \backsim \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta NMP\)
-
C.
\(\Delta ABC \backsim \Delta NPM\)
-
D.
\(\Delta BAC \backsim \Delta MNP\)
Với điều kiện nào sau đây thì \(\Delta ABC \backsim \Delta MNP\)
-
A.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
-
B.
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{MN}} = \frac{{BC}}{{NP}}\) .
-
C.
\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{MN}}\) .
-
D.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
Cho \(\Delta ABC \backsim \Delta MNP\) biết \(AB = 3cm;BC = 4cm;MN = 6cm;MP = 5cm\) . Khi đó:
-
A.
AC = 8cm; NP = 2,5cm
-
B.
AC = 2,5cm; NP = 8cm
-
C.
AC = 2,5cm; NP = 10cm
-
D.
AC = 10cm; NP = 2cm
Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;
MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là
-
A.
\(\frac{3}{5}\) .
-
B.
2.
-
C.
\(\frac{5}{6}\) .
-
D.
\(\frac{1}{2}\) .
Cho hai tam giác ABC và DEF có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?
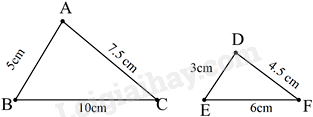
-
A.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta {\rm{FED}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
D.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
A.
\(\Delta ABC \backsim \Delta DBC\)
-
B.
\(\Delta A{\rm{D}}B \backsim \Delta DBC\)
-
C.
\(\Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\)
-
D.
\(\Delta A{\rm{D}}C \backsim \Delta ABC\)
Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là
-
A.
\(\frac{1}{2}\) .
-
B.
3.
-
C.
\(\frac{1}{3}\) .
-
D.
2.
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) khẳng định nào sau đây là sai
-
A.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
-
B.
\(\frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) .
-
C.
\(\frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) .
-
D.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\) . Cho biết \(\Delta ABC \backsim \Delta A'B'C'\) và cạnh nhỏ nhất của \(\Delta A'B'C'\) bằng 2cm. Độ dài các cạnh còn lại của tam giác \(A'B'C'\) lần lượt là
-
A.
3cm; 4cm
-
B.
2,5cm; 4cm.
-
C.
3cm; 2cm
-
D.
2,5cm; 3cm.
Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:
-
A.
x = 12cm; y = 18cm
-
B.
x = 9cm; y = 24cm
-
C.
x = 18cm; y = 12cm
-
D.
x = 8cm; y = 27cm
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là
-
A.
220cm
-
B.
900cm
-
C.
225cm
-
D.
150cm
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
-
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Cho \(\Delta ABC\) vuông tại A, đường cao \(AH(H \in BC)\) . Biết AB = 3cm, AC = 6cm,
AH = 2cm, HC = 4cm. Hệ thức nào sau đây đúng:
-
A.
\(A{C^2} = CH.BH\)
-
B.
\(AB.AH = HC.AC\)
-
C.
\(AB.HC = AH.AC\)
-
D.
\(AB.AC = AH.HC\)
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) thì
-
A.
\(\Delta ABC\backsim \Delta DEF\) .
-
B.
\(\Delta CAB\backsim \Delta DEF\) .
-
C.
\(\Delta ABC\backsim \Delta DFE\) .
-
D.
\(\Delta CAB \backsim \Delta DFE\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}={{70}^{\circ }}\) , \(\widehat{C}={{60}^{\circ }}\) , \(\widehat{E}={{50}^{\circ }}\) , \(\widehat{F}={{70}^{\circ }}\) thì
-
A.
\(\Delta ACB\,\,\backsim \,\,\Delta FED\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta FED\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta DEF\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta DFE\) .
Cho \(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) (g – g ). Khẳng định nào sau đây đúng
-
A.
\(\widehat{A}=\widehat{{{B}'}}\) .
-
B.
\(AB={A}'{B}'\) .
-
C.
\(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\) .
-
D.
\(\frac{AB}{AC}=\frac{{A}'{C}'}{{A}'{B}'}\) .
-
A.
\(\Delta HIG\backsim \Delta DEF\) .
-
B.
\(\Delta IGH\backsim \Delta DEF\) .
-
C.
\(\Delta HIG\backsim \Delta DFE\) .
-
D.
\(\Delta HGI\backsim \Delta DEF\) .
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
-
A.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
có hai cặp cạnh tương ứng bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Nếu \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat{A}=\widehat{N}\) ; \(\widehat{B}=\widehat{M}\) thì
-
A.
\(\Delta ABC\backsim \,\Delta MNP\) .
-
B.
\(\Delta CAB\backsim \Delta NMP\) .
-
C.
\(\Delta ABC\backsim \Delta PMN\) .
-
D.
\(\Delta ABC\backsim \Delta NMP\) .
Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) . Để \(\Delta MNP\,\backsim \,\Delta DEF\) thì cần thêm điều kiện
-
A.
\(\widehat{E}=50{}^\circ \) .
-
B.
\(\widehat{F}=60{}^\circ \) .
-
C.
\(\widehat{F}=40{}^\circ \) .
-
D.
\(\widehat{E}=40{}^\circ \)
Nếu \(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=70{}^\circ \) ; \(\widehat{E}=60{}^\circ \) ; \(\widehat{S}=70{}^\circ \) ; \(\widehat{K}=50{}^\circ \) thì
-
A.
\(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
B.
\(\frac{DE}{SR}=\frac{DF}{RK}=\frac{EF}{SK}\) .
-
C.
\(\frac{DE}{SR}=\frac{DF}{SR}=\frac{EF}{RK}\) .
-
D.
\(\frac{DE}{RK}=\frac{DF}{SK}=\frac{EF}{SR}\)
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Cho hình thang \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\), \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khẳng định nào sau đây đúng
-
A.
\({\rm{\Delta }}OAB \backsim \,\Delta ODC\).
-
B.
\({\rm{\Delta }}CAB \backsim {\rm{\Delta }}CDA\).
-
C.
\({\rm{\Delta }}OAB \backsim {\rm{\Delta }}OCD\).
-
D.
\({\rm{\Delta }}OAD \backsim {\rm{\Delta }}OBC\).
Cho hình thang \(ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)\), \(\widehat {ADB} = \widehat {BCD}\), \(AB = 2\,{\rm{cm}}\), \(BD = \sqrt 5 \,{\rm{cm}}\). Độ dài đoạn thẳng \(CD\) là

-
A.
\(2\sqrt 5 \,{\rm{cm}}\).
-
B.
\(\sqrt 5 - 2\,{\rm{cm}}\).
-
C.
\(\frac{{\sqrt 5 }}{2}\,{\rm{cm}}\).
-
D.
\(2,5\,{\rm{cm}}\).
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Cho hình vẽ, biết \(\widehat {ACB} = \widehat {ABD}\), \(AB = 3\,{\rm{cm}}\), \(AC = 4,5\,{\rm{cm}}\). Độ dài đoạn thẳng \(AD\) là
-
A.
\(2\,{\rm{cm}}\).
-
B.
\(2,5\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(1,5\,{\rm{cm}}\).
Lời giải và đáp án
Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :
-
A.
\(3cm;4cm;6cm\) và \(9cm;15cm;18cm\) .
-
B.
\(4cm;5cm;6cm\) và \(8cm;10cm;12cm\) .
-
C.
\(6cm;5cm;6cm\) và \(3cm;5cm;3cm\) .
-
D.
\(5cm;7cm;1dm\) và \(10cm;14cm;18cm\) .
Đáp án : B
Vì \(\frac{3}{8} = \frac{6}{{18}}\left( { = \frac{1}{2}} \right) \ne \frac{4}{{15}}\) nên hai tam giác có độ dài các cạnh 3cm; 4cm; 6cm và 9 cm; 15cm; 18 cm không đồng dạng với nhau
Vì \(\frac{4}{8} = \frac{5}{{10}} = \frac{6}{{12}}\) nên hai tam giác có độ dài các cạnh là 4cm; 5cm; 6cm và 8cm; 10cm; 12cm đồng dạng với nhau theo trường hợp thứ nhất. Chọn B
Vì \(\frac{6}{3} = \frac{6}{3} \ne \frac{5}{5}\) nên hai tam giác có độ dài các cạnh là 6cm; 5 cm; 6 cm và 3cm; 5cm; 3 cm không đồng dạng với nhau.
Vì \(\frac{5}{{10}} = \frac{7}{{14}} \ne \frac{{10}}{{18}}\) nên hai tam giác có độ dài các cạnh là 5cm; 7cm; 1 dm và 10cm; 14cm; 18 cm không đồng dạng với nhau.
Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?
-
A.
\(\Delta ABC \backsim \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta NMP\)
-
C.
\(\Delta ABC \backsim \Delta NPM\)
-
D.
\(\Delta BAC \backsim \Delta MNP\)
Đáp án : C
Vì \(\frac{{AB}}{{NP}} = \frac{6}{8} = \frac{3}{4};\frac{{AC}}{{NM}} = \frac{9}{{12}} = \frac{3}{4};\frac{{BC}}{{PM}} = \frac{{12}}{{16}} = \frac{3}{4}\)
Nên \(\frac{{AB}}{{NP}} = \frac{{AC}}{{NM}} = \frac{{BC}}{{PM}} = \frac{3}{4} \Rightarrow \Delta ABC \backsim \Delta NPM\)
Với điều kiện nào sau đây thì \(\Delta ABC \backsim \Delta MNP\)
-
A.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
-
B.
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{MN}} = \frac{{BC}}{{NP}}\) .
-
C.
\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{MN}}\) .
-
D.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
Đáp án : A
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} \Rightarrow \Delta ABC \backsim \Delta MNP\)
Cho \(\Delta ABC \backsim \Delta MNP\) biết \(AB = 3cm;BC = 4cm;MN = 6cm;MP = 5cm\) . Khi đó:
-
A.
AC = 8cm; NP = 2,5cm
-
B.
AC = 2,5cm; NP = 8cm
-
C.
AC = 2,5cm; NP = 10cm
-
D.
AC = 10cm; NP = 2cm
Đáp án : B
\(\begin{array}{l}\Delta ABC \backsim \Delta MNP\\ \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\\ \Rightarrow \frac{3}{6} = \frac{{AC}}{5} = \frac{4}{{NP}}\\ \Rightarrow AC = \frac{{3.5}}{6} = 2,5(cm)\\ \Rightarrow NP = \frac{{4.6}}{3} = 8(cm)\end{array}\)
Vậy AC = 2,5cm; NP = 8cm
Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;
MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là
-
A.
\(\frac{3}{5}\) .
-
B.
2.
-
C.
\(\frac{5}{6}\) .
-
D.
\(\frac{1}{2}\) .
Đáp án : D
Vì \(\frac{{AB}}{{MN}} = \frac{3}{6} = \frac{1}{2};\frac{{AC}}{{MP}} = \frac{5}{{10}} = \frac{1}{2};\frac{{BC}}{{NP}} = \frac{7}{{14}} = \frac{1}{2}\)
Suy ra: \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = \frac{1}{2} \Rightarrow \Delta ABC \backsim \Delta MNP\) theo tỉ số đồng dạng là \(\frac{1}{2}\)
Vì \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = \frac{{AB + AC + BC}}{{MN + MP + NP}} = \frac{1}{2}\)
\( \Rightarrow \frac{{C{V_{\Delta ABC}}}}{{C{V_{\Delta MNP}}}} = \frac{1}{2}\)
Cho hai tam giác ABC và DEF có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?

-
A.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta {\rm{FED}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
D.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
Đáp án : D
Vì \(\frac{{AB}}{{DE}} = \frac{5}{3};\frac{{AC}}{{DF}} = \frac{{7,5}}{{4,5}} = \frac{5}{3};\frac{{BC}}{{EF}} = \frac{{10}}{6} = \frac{5}{3}\)
Suy ra: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{5}{3} \Rightarrow \Delta ABC \backsim \Delta DEF\) với tỉ số đồng dạng là \(\frac{5}{3}\)
Tỉ số của các cạnh tương ứng là tỉ số đồng dạng của hai tam giác.
-
A.
\(\Delta ABC \backsim \Delta DBC\)
-
B.
\(\Delta A{\rm{D}}B \backsim \Delta DBC\)
-
C.
\(\Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\)
-
D.
\(\Delta A{\rm{D}}C \backsim \Delta ABC\)
Đáp án : B
Vì \(\frac{{AD}}{{DB}} = \frac{4}{8} = \frac{1}{2};\frac{{AB}}{{DC}} = \frac{6}{{12}} = \frac{1}{2};\frac{{B{\rm{D}}}}{{BC}} = \frac{8}{{16}} = \frac{1}{2}\)
Suy ra: \(\frac{{AD}}{{DB}} = \frac{{AB}}{{DC}} = \frac{{DB}}{{BC}} = \frac{1}{2} \Rightarrow \Delta A{\rm{D}}B \backsim \Delta DBC\) (Trường hợp đồng dạng thứ nhất),
Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là
-
A.
\(\frac{1}{2}\) .
-
B.
3.
-
C.
\(\frac{1}{3}\) .
-
D.
2.
Đáp án : C
Vì \(\frac{{MN}}{{AB}} = \frac{1}{3};\frac{{MP}}{{AC}} = \frac{2}{6} = \frac{1}{3};\frac{{NP}}{{BC}} = \frac{3}{9} = \frac{1}{3}\)
Suy ra: \(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{1}{3}\)
Do đó \(\Delta MNP \backsim \Delta ABC\) theo tỉ số đồng dạng \(\frac{1}{3}\) .
Vì \(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}}\) nên áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{{MN + MP + NP}}{{AB + AC + BC}} = \frac{{C{V_{\Delta MNP}}}}{{C{V_{\Delta ABC}}}} = \frac{1}{3}\)
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) khẳng định nào sau đây là sai
-
A.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
-
B.
\(\frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) .
-
C.
\(\frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) .
-
D.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
Đáp án : D
\(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) \( \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) (các cạnh tương ứng)
\( \Rightarrow \frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) (Tính chất tỉ lệ thức)
\( \Rightarrow \frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) (Tính chất tỉ lệ thức)
\( \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) là khẳng định sai
Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\) . Cho biết \(\Delta ABC \backsim \Delta A'B'C'\) và cạnh nhỏ nhất của \(\Delta A'B'C'\) bằng 2cm. Độ dài các cạnh còn lại của tam giác \(A'B'C'\) lần lượt là
-
A.
3cm; 4cm
-
B.
2,5cm; 4cm.
-
C.
3cm; 2cm
-
D.
2,5cm; 3cm.
Đáp án : D
Theo đầu bài tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\)
Và \(\Delta ABC \backsim \Delta A'B'C'\) nên \(\Delta A'B'C'\) cũng có độ dài các cạnh tỉ lệ với \(4:5:6\)
Giả sử \(A'B' < A'C' < B'C' \Rightarrow A'B' = 2cm\)
\( \Rightarrow \frac{{A'B'}}{4} = \frac{{A'C'}}{5} = \frac{{B'C'}}{6} \Rightarrow \frac{{A'C'}}{5} = \frac{{B'C'}}{6} = \frac{2}{4}\)
\(\begin{array}{l} \Rightarrow A'C' = \frac{{5.2}}{4} = 2,5(cm)\\ \Rightarrow B'C' = \frac{{6.2}}{4} = 3(cm)\end{array}\)
Độ dài các cạnh còn lại của tam giác A’B’C’ lần lượt là 2,5cm ; 3cm.
Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:
-
A.
x = 12cm; y = 18cm
-
B.
x = 9cm; y = 24cm
-
C.
x = 18cm; y = 12cm
-
D.
x = 8cm; y = 27cm
Đáp án : A
Theo đề bài:
Tam giác thứ nhất có cạnh lần lượt là 8; x; y (8 < x < y)
Tam giác thứ hai có cạnh lần lượt là x; y ; 27 ( x < y < 27)
Để hai tam giác đồng dạng cần:
\(\begin{array}{l}\frac{8}{x} = \frac{x}{y} = \frac{y}{{27}}\\ \Rightarrow xy = 8.27;{x^2} = 8y\\ \Rightarrow y = \frac{{8.27}}{x};{x^2} = 8.\frac{{8.27}}{x} \Rightarrow {x^3} = 64.27 = {\left( {4.3} \right)^3}\end{array}\)
Vậy x = 12cm; y = 18cm
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là
-
A.
220cm
-
B.
900cm
-
C.
225cm
-
D.
150cm
Đáp án : C
Vì P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Nên PQ, QR, RP lần lượt là đường trung bình của các tam giác AOB; BOC; AOC. Nên ta có:
\(\frac{{PQ}}{{AB}} = \frac{{Q{\rm{R}}}}{{BC}} = \frac{{P{\rm{R}}}}{{AC}} = \frac{1}{2}\)
Suy ra: \(\Delta PQ{\rm{R}} \backsim \Delta ABC\)
Vì:
\(\begin{array}{l}\frac{{PQ}}{{AB}} = \frac{{Q{\rm{R}}}}{{BC}} = \frac{{P{\rm{R}}}}{{AC}} = \frac{{PQ + Q{\rm{R}} + P{\rm{R}}}}{{AB + BC + AC}} = \frac{{C{V_{\Delta PQ{\rm{R}}}}}}{{C{V_{\Delta ABC}}}}\\ \Rightarrow \frac{{C{V_{\Delta PQ{\rm{R}}}}}}{{C{V_{\Delta ABC}}}} = \frac{1}{2} \Rightarrow C{V_{\Delta PQ{\rm{R}}}} = \frac{{C{V_{\Delta ABC}}}}{2} = \frac{{450}}{2} = 225(cm)\end{array}\)
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Đáp án : D
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc – cạnh nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
Đáp án : B
Ta có: \(\frac{{DE}}{{IL}} = \frac{{EF}}{{LK}}\left( {\frac{{10}}{{20}} = \frac{4}{8} = \frac{1}{2}} \right).\)
Để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)}}\) thì \(\hat E = \hat L\) (hai góc tạo bởi các cặp cạnh)
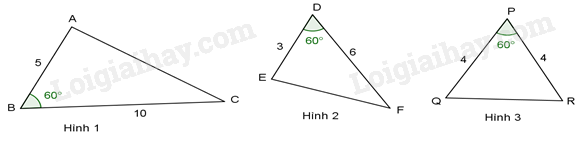
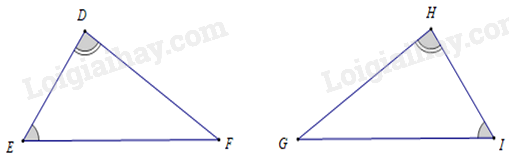
-
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
Đáp án : A
Ta có: \(\frac{{BA}}{{BC}} = \frac{5}{{10}} = \frac{1}{2},\frac{{DE}}{{DF}} = \frac{3}{6} = \frac{1}{2},\frac{{PQ}}{{PR}} = \frac{4}{4} = 1\) ,
Xét \(\Delta ABC\) và \(\Delta EDF\) ta có: \(\frac{{BA}}{{BC}} = \frac{{DE}}{{DF}} = \frac{1}{2} \Leftrightarrow \frac{{BA}}{{DE}} = \frac{{BC}}{{DF}}\) và \(\hat B = \hat D = {60^0}(gt)\)
\( \Rightarrow \Delta ABC \backsim \Delta EDF(c - g - c)\)
Hình 1 và hình 2 là hai tam giác đồng dạng
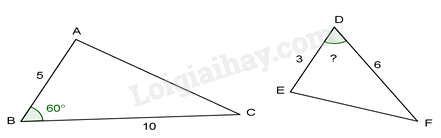
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Đáp án : B
Ta có: \(\frac{{BA}}{{BC}} = \frac{5}{{10}} = \frac{1}{2},\frac{{DE}}{{DF}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{BA}}{{BC}} = \frac{{DE}}{{DF}} = \frac{1}{2} \Leftrightarrow \frac{{BA}}{{DE}} = \frac{{BC}}{{DF}}\)
Để hai tam giác đã cho đồng dạng thì \(\hat B = \hat D = {60^0}\) .
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Đáp án : A
Ta có: \(\widehat A = \widehat {{A'}}\) và \(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}\) thì \(\Delta {A'}{B'}{C'} \backsim \Delta ABC\) (c-g-c)
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Đáp án : D
\(\Delta MNP \backsim \Delta KIH \Rightarrow \frac{{MN}}{{KI}} = \frac{{MP}}{{KH}} \Leftrightarrow \frac{2}{{KI}} = \frac{8}{4} \Rightarrow KI = 1(cm)\)
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Đáp án : C
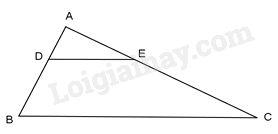
Xét \(\Delta ADE\) và \(\Delta ABC\) ta có: \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) (gt); \(\hat A\) chung
\( \Rightarrow \Delta ADE \backsim \Delta ABC(c - g - c)\)
\( \Rightarrow \widehat {ADE} = \widehat {ABC}\) (cặp góc tương ứng)
\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\)
\( \Rightarrow DE//BC\) (định lý Ta lét đảo)
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
Đáp án : B
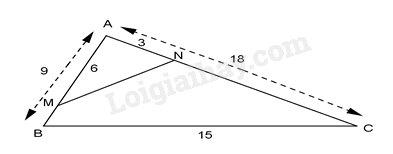
Ta có: \(\frac{{AN}}{{AB}} = \frac{3}{9} = \frac{1}{3},\frac{{AM}}{{AC}} = \frac{6}{{18}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{1}{3}\)
Xét \(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}(cmt);\hat A\) chung
nên \( \Delta ANM \backsim \Delta ABC(c - g - c)\)
suy ra \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{{MN}}{{CB}} = \frac{1}{3}\)
\(\frac{{MN}}{{15}} = \frac{1}{3}\)
\(MN = \frac{{15}}{3} = 5(cm).\)
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
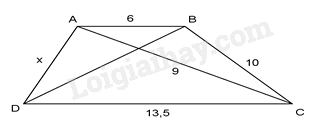
Đáp án : A
Ta có \(\frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3},\frac{{AC}}{{CD}} = \frac{9}{{13,5}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{AC}}{{CD}} = \frac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có: \(\frac{{AB}}{{AC}} = \frac{{AC}}{{CD}}(cmt),\widehat {BAC} = \widehat {ACD}\) (so le trong, AB//CD )
\(\begin{array}{l} \Rightarrow \Delta ABC \backsim \Delta CAD(c - g - c)\\ \Rightarrow \frac{{AB}}{{AC}} = \frac{{CA}}{{CD}} = \frac{{BC}}{{AD}} = \frac{2}{3}\\ \Rightarrow \frac{{10}}{x} = \frac{2}{3} \Rightarrow x = \frac{{10.3}}{2} = 15\end{array}\)
Cho \(\Delta ABC\) vuông tại A, đường cao \(AH(H \in BC)\) . Biết AB = 3cm, AC = 6cm,
AH = 2cm, HC = 4cm. Hệ thức nào sau đây đúng:
-
A.
\(A{C^2} = CH.BH\)
-
B.
\(AB.AH = HC.AC\)
-
C.
\(AB.HC = AH.AC\)
-
D.
\(AB.AC = AH.HC\)
Đáp án : C

Xét \(\Delta ABC\) và \(\Delta HAC\) có: \(\frac{{AB}}{{AC}} = \frac{3}{6} = \frac{1}{2},\frac{{AH}}{{HC}} = \frac{2}{4} = \frac{1}{2}\)
\(\begin{array}{l} \Rightarrow \frac{{AB}}{{AC}} = \frac{{AH}}{{HC}} = \frac{1}{2}\\ \Rightarrow AB.HC = AH.AC\end{array}\)
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Đáp án : B
Ta có tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng \(\frac{{M{M'}}}{{E{E '}}} = k\)
Tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng.
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Đáp án : B
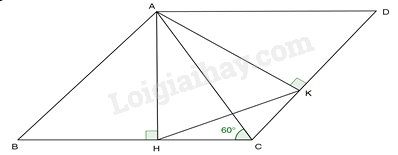
Vì \(AD.AH = AB.AK( = {S_{ABCD}})\) nên \(\frac{{AH}}{{AK}} = \frac{{AB}}{{AD}} = \frac{{AB}}{{BC}}\)
Ta lại có AB//CD (vì ABCD là hình bình hành) mà \(AK \bot DC \Leftrightarrow AK \bot AB \Rightarrow \widehat {BAK} = {90^0}\)
Từ đó \(\widehat {HAK} = \widehat {ABC}\) (cùng phụ với \(\widehat {BAH}\) )
Nên \(\Delta AKH \backsim \Delta BCA(c - g - c) \Rightarrow \widehat {AKH} = \widehat {ACB} = {60^0}\)
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Đáp án : C
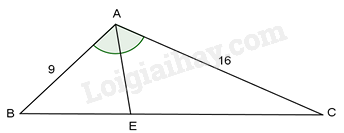
Kẻ đường phân giác AE của \(\Delta ABC\) . Theo tính chất đường phân giác, ta có:
\(\frac{{BE}}{{EC}} = \frac{{AB}}{{AC}} = \frac{9}{{16}}\) hay \(\frac{{BE}}{{AB}} = \frac{{CE}}{{AC}}\)
Nên \(\frac{{BE + EC}}{{AB+AC}} = \frac{{20}}{{9+16}}=\frac{4}{5}\)
Hay \(\frac{{CE}}{{AC}} = \frac{{CE}}{{16}} =\frac{4}{5} \Rightarrow EC = 12,8(cm)\)
Xét \(\Delta ACB\) và \(\Delta ECA\) có: \(\hat C\) là góc chung
\(\frac{{AC}}{{EC}} = \frac{{CB}}{{CA}}\) (vì \(\frac{{16}}{{12,8}} = \frac{{20}}{{16}})\)
Do đó \(\Delta ACB \backsim \Delta ECA\) (c-g-c) suy ra \(\hat B = \widehat {CAE}\) tức là \(\hat B = \frac{{\hat A}}{2}\)
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
Đáp án : C
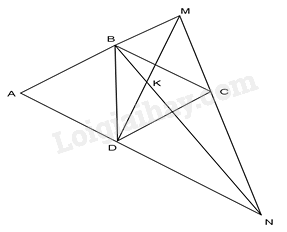
Do BC//AN (Vì \(N \in AD\) ) nên ta có: \(\frac{{MB}}{{AB}} = \frac{{MC}}{{NC}}\) (1)
Do CD//AM (Vì \(M \in AB\) ) nên ta có: \(\frac{{MC}}{{NC}} = \frac{{AD}}{{DN}}\) (2)
Từ (1) và (2) ta có: \(\frac{{MB}}{{AB}} = \frac{{AD}}{{DN}}\)
\(\Delta ABD\) có AB = AD (định nghĩa hình thoi) và \(\hat A = {60^0}\) nên \(\Delta ABD\) là tam giác đều
suy ra \(AB = BD = DA\)
Từ \(\frac{{MB}}{{AB}} = \frac{{AD}}{{DN}}(cmt) \) suy ra \(\frac{{MB}}{{BD}} = \frac{{BD}}{{DN}}\)
Mặt khác \(\widehat {MBD} = \widehat {BDN} = {120^0}\) (hai góc kề bù với góc \(\widehat {ABD} = \widehat {ADB} = {60^0}\)
Xét \(\Delta MBD\) và \(\Delta BDN\) có: \(\frac{{MB}}{{BD}} = \frac{{BD}}{{DN}},\widehat {MBD} = \widehat {BDN}\)
suy ra \( \Delta MBD \backsim \Delta BDN(c - g - c)\) do đó \( \widehat {BMD} = \widehat {DBN}\)
Xét \(\Delta MBD\) và \(\Delta KBD\) có: \(\widehat {MBD} = \widehat {DBN},\widehat {BDM}\) chung
suy ra \(\widehat {BKD} = \widehat {MDB} = {120^0}\)
Vậy \(\widehat {BKD} = {120^0}\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) thì
-
A.
\(\Delta ABC\backsim \Delta DEF\) .
-
B.
\(\Delta CAB\backsim \Delta DEF\) .
-
C.
\(\Delta ABC\backsim \Delta DFE\) .
-
D.
\(\Delta CAB \backsim \Delta DFE\)
Đáp án : A
Xét \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) nên \(\Delta ABC\backsim \Delta DEF\) (g – g)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}={{70}^{\circ }}\) , \(\widehat{C}={{60}^{\circ }}\) , \(\widehat{E}={{50}^{\circ }}\) , \(\widehat{F}={{70}^{\circ }}\) thì
-
A.
\(\Delta ACB\,\,\backsim \,\,\Delta FED\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta FED\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta DEF\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta DFE\) .
Đáp án : B
\(\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}={{180}^{\circ }}\Rightarrow {{70}^{\circ }}+\widehat{B}+{{60}^{\circ }}={{180}^{\circ }}\Leftrightarrow \widehat{B}={{50}^{\circ }}\) .
\(\Delta ABC\) và \(\Delta FED\) có \(\widehat{A}=\widehat{F}=70{}^\circ \) , \(\widehat{B}=\widehat{E}=50{}^\circ \) nên \(\Delta ABC\,\backsim \,\Delta FED\) (g – g ).
Cho \(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) (g – g ). Khẳng định nào sau đây đúng
-
A.
\(\widehat{A}=\widehat{{{B}'}}\) .
-
B.
\(AB={A}'{B}'\) .
-
C.
\(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\) .
-
D.
\(\frac{AB}{AC}=\frac{{A}'{C}'}{{A}'{B}'}\) .
Đáp án : C
\(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) suy ra \(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\)
-
A.
\(\Delta HIG\backsim \Delta DEF\) .
-
B.
\(\Delta IGH\backsim \Delta DEF\) .
-
C.
\(\Delta HIG\backsim \Delta DFE\) .
-
D.
\(\Delta HGI\backsim \Delta DEF\) .
Đáp án : A
\(\Delta HIG\) và \(\Delta DEF\) có \(\widehat{H}=\widehat{D}\) , \(\widehat{I}=\widehat{E}\) (gt) nên \(\Delta HIG\,\,\backsim \Delta DEF\) (g – g ).
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
-
A.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
có hai cặp cạnh tương ứng bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Nếu \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat{A}=\widehat{N}\) ; \(\widehat{B}=\widehat{M}\) thì
-
A.
\(\Delta ABC\backsim \,\Delta MNP\) .
-
B.
\(\Delta CAB\backsim \Delta NMP\) .
-
C.
\(\Delta ABC\backsim \Delta PMN\) .
-
D.
\(\Delta ABC\backsim \Delta NMP\) .
Đáp án : D
\(\Delta ABC\) và \(\Delta NMP\) có \(\widehat{A}=\widehat{N}\) , \(\widehat{B}=\widehat{M}\) nên \(\Delta ABC\backsim \Delta NMP\) (g – g ).
Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) . Để \(\Delta MNP\,\backsim \,\Delta DEF\) thì cần thêm điều kiện
-
A.
\(\widehat{E}=50{}^\circ \) .
-
B.
\(\widehat{F}=60{}^\circ \) .
-
C.
\(\widehat{F}=40{}^\circ \) .
-
D.
\(\widehat{E}=40{}^\circ \)
Đáp án : D
\(\Delta MNP\) có \(\widehat{M}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) \(\Rightarrow \widehat{N}=40{}^\circ \) .
\(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}\) (gt) cần thêm điều kiện \(\widehat{E}=40{}^\circ \) thì \(\Rightarrow \widehat{N}=\widehat{E}=40{}^\circ \)
Lúc này \(\Delta MNP\backsim \Delta DEF\) (g – g ).
Nếu \(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=70{}^\circ \) ; \(\widehat{E}=60{}^\circ \) ; \(\widehat{S}=70{}^\circ \) ; \(\widehat{K}=50{}^\circ \) thì
-
A.
\(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
B.
\(\frac{DE}{SR}=\frac{DF}{RK}=\frac{EF}{SK}\) .
-
C.
\(\frac{DE}{SR}=\frac{DF}{SR}=\frac{EF}{RK}\) .
-
D.
\(\frac{DE}{RK}=\frac{DF}{SK}=\frac{EF}{SR}\)
Đáp án : A
\(\Delta DEF\) có \(\widehat{D}+\widehat{E}+\widehat{F}=180{}^\circ \Rightarrow 70{}^\circ +60{}^\circ +\widehat{F}=180{}^\circ \Rightarrow \widehat{F}=50{}^\circ \) .
\(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=\widehat{S}=70{}^\circ \) và \(\widehat{F}=\widehat{K}=50{}^\circ \) nên \(\Delta DEF\,\backsim \,\Delta SRK\) (g – g).
Suy ra \(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
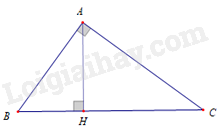
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Đáp án : D
\(\Delta ABC\) và \(\Delta HBA\) có góc \( \widehat{B}\) chung, \(\widehat{BAC}=\widehat{AHB}=90{}^\circ \) nên \(\Delta ABC\,\backsim \Delta HBA\) (g – g)
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Đáp án : C

Xét \(\Delta HCA\) và \(\Delta HAB\) có:
\(\widehat {HAC} = \widehat B\) (Vì cùng phụ với \(\widehat {HAB}\) ); \(\widehat {CHA} = \widehat {AHB} = 90^\circ \)
nên \(\Delta HCA\,\, \backsim \,\Delta HAB\) (g – g ) \( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Leftrightarrow A{H^2} = BH.CH\).
Cho hình thang \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\), \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khẳng định nào sau đây đúng
-
A.
\({\rm{\Delta }}OAB \backsim \,\Delta ODC\).
-
B.
\({\rm{\Delta }}CAB \backsim {\rm{\Delta }}CDA\).
-
C.
\({\rm{\Delta }}OAB \backsim {\rm{\Delta }}OCD\).
-
D.
\({\rm{\Delta }}OAD \backsim {\rm{\Delta }}OBC\).
Đáp án : C

Vì \(AB\,{\rm{//}}\,CD\) (gt) nên \(\widehat {ABO} = \widehat {ODC}\) (cặp góc so le trong) .
\({\rm{\Delta }}OAB\) và \(\,\Delta OCD\) có:
\(\widehat {ABO} = \widehat {ODC}\) (chứng minh trên); \(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Nên \({\rm{\Delta }}OAB \backsim \,\Delta OCD\) (g – g ).
Cho hình thang \(ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)\), \(\widehat {ADB} = \widehat {BCD}\), \(AB = 2\,{\rm{cm}}\), \(BD = \sqrt 5 \,{\rm{cm}}\). Độ dài đoạn thẳng \(CD\) là

-
A.
\(2\sqrt 5 \,{\rm{cm}}\).
-
B.
\(\sqrt 5 - 2\,{\rm{cm}}\).
-
C.
\(\frac{{\sqrt 5 }}{2}\,{\rm{cm}}\).
-
D.
\(2,5\,{\rm{cm}}\).
Đáp án : D
Vì \(AB\,{\rm{//}}\,CD \Rightarrow \widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong).
Xét \(\Delta \,ADB\) và \(\Delta \,BCD\) có:
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên); \(\widehat {ADB} = \widehat {BCD}\) (gt)
Nên \(\Delta \,ADB\, \backsim \Delta BCD\) (g – g ).
\( \Rightarrow \frac{{AB}}{{BD}} = \frac{{DB}}{{CD}} \Leftrightarrow \frac{2}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{{CD}} \Leftrightarrow CD = \frac{{\sqrt 5 .\sqrt 5 }}{2} = \frac{5}{2} = 2,5\,\,\left( {{\rm{cm}}} \right)\).
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Đáp án : D
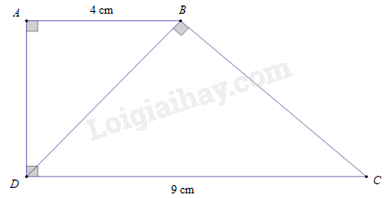
Ta có \(AB\,{\rm{//}}\,{\rm{CD}}\) ( vì cùng vuông góc với \(A{\rm{D}}\)).\( \Rightarrow \widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(\Delta ABD\) và \(\Delta BDC\) có:
\(\widehat {BAD} = \widehat {DBC} = 90^\circ \); \(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Nên \(\Delta \,ABD\,\, \backsim \,\Delta BDC\) (g – g) \( \Rightarrow \frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} \Rightarrow B{D^2} = AB.DC = 4.9 = 36 \Rightarrow BD = 6\,\,\left( {{\rm{cm}}} \right)\).
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Đáp án : C
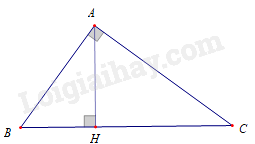
Xét \(\Delta HCA\) và \(\Delta HAB\) có :
\(\widehat {HAC} = \widehat B\) (Vì cùng phụ với \(\widehat {HAB}\)) ; \(\widehat {CHA} = \widehat {AHB} = 90^\circ \)
nên \(\Delta HCA\, \backsim \Delta HAB\) (g – g ) \( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Leftrightarrow A{H^2} = BH.CH\) .
\( \Leftrightarrow A{H^2} = 4.9 = 36 \Rightarrow AH = 6\,\left( {{\rm{cm}}} \right)\) .
Cho hình vẽ, biết \(\widehat {ACB} = \widehat {ABD}\), \(AB = 3\,{\rm{cm}}\), \(AC = 4,5\,{\rm{cm}}\). Độ dài đoạn thẳng \(AD\) là

-
A.
\(2\,{\rm{cm}}\).
-
B.
\(2,5\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(1,5\,{\rm{cm}}\).
Đáp án : A
Chứng minh \(\Delta ABC\, \backsim \Delta ADB\) (g– g ) \( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{AB}} \Leftrightarrow AD = \frac{{AB.AB}}{{AC}} = \frac{{3.3}}{{4,5}} = 2\,({\rm{cm)}}\)
Xét \(\Delta ABC\) và \(\Delta ADB\) có:
Góc \(A\) chung, \(\widehat {ACB} = \widehat {ABD}\) (gt)
Nên \(\Delta ABC\, \backsim \,\Delta ADB\) (g– g ) \( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{AB}} \Leftrightarrow AD = \frac{{AB.AB}}{{AC}} = \frac{{3.3}}{{4,5}} = 2\,({\rm{cm)}}\)
Luyện tập và củng cố kiến thức Bài 35: Định lí Pythagore và ứng dụng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 37: Hình đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 33: Hai tam giác đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 39: Hình chóp tứ giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 38: Hình chóp tam giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 37: Hình đồng dạng Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 35: Định lí Pythagore và ứng dụng Toán 8 Kết nối tri thức











Danh sách bình luận