Trắc nghiệm Bài 27: Khái niệm hàm số và đồ thị của hàm số Toán 8 Kết nối tri thức
Đề bài
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y.
Chọn đáp án đúng
-
A.
y được gọi là hàm số của biến số x
-
B.
x được gọi là hàm số của biến số y
-
C.
Cả A và B đều đúng
-
D.
Cả A và B đều sai
-
A.
y là hàm số của biến số x
-
B.
x là hàm số của biến số y
-
C.
y tỉ lệ thuận với x
-
D.
y tỉ lệ nghịch với x
Trong các công thức dưới đây, công thức nào thể hiện y không phải là hàm số của x?
-
A.
\(y = x + 1\)
-
B.
\(y = \frac{1}{2}x\)
-
C.
\(y = {x^2}\)
-
D.
\({y^2} = x\)
Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y...f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
Đáp án đúng điền vào “…”.
-
A.
\( > \)
-
B.
\( < \)
-
C.
\( = \)
-
D.
\( \ne \)
Nhiệt độ N của một nhà máy ấp trứng vịt được cài đặt luôn bằng 37oC không thay đổi theo thời gian t. Khi đó, công thức xác định hàm số N(t) của nhiệt độ theo thời gian là:
-
A.
\(N\left( t \right) = 37\)
-
B.
\(N\left( t \right) > 37\)
-
C.
\(N\left( t \right) < 37\)
-
D.
\(N\left( t \right) \ge 37\)
Một hàm số được cho bởi công thức \(f\left( x \right) = \frac{{ - 1}}{2}x + 5.\) Khẳng định nào sau đây là đúng?
-
A.
\(f\left( 1 \right) > f\left( 2 \right)\)
-
B.
\(f\left( 1 \right) = f\left( 2 \right)\)
-
C.
\(f\left( 1 \right) < f\left( 2 \right)\)
-
D.
\(f\left( 1 \right) \le f\left( 2 \right)\)
Một hình lập phương có độ dài cạnh là x (cm) và thể tích là \(V\left( {c{m^3}} \right)\).
Chọn khẳng định đúng.
-
A.
\(V = {x^2},\) V là hàm số của biến số x.
-
B.
\(V = {x^2},\) V là không hàm số của biến số x.
-
C.
\(V = {x^3},\) V là hàm số của biến số x.
-
D.
\(V = {x^3},\) V không là hàm số của biến số x.
Nhà bác học Galileo Galilei là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y(m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}.\) Quãng đường mà vật đó chuyển động được sau 4 giây là:
-
A.
60m
-
B.
70m
-
C.
80m
-
D.
90m
Cho hàm số \(f\left( x \right) = 3{x^4} - 3{x^2} - 1.\) So sánh f(x) và f(-x)
-
A.
\(f\left( x \right) < f\left( { - x} \right)\)
-
B.
\(f\left( x \right) = f\left( { - x} \right)\)
-
C.
\(f\left( x \right) > f\left( { - x} \right)\)
-
D.
Không so sánh được f(x) và f(-x)
Cho hàm số \(f\left( x \right) = 30x + 100.\) Để \(f\left( x \right) = 190\) thì giá trị của x là:
-
A.
\(x = - 4\)
-
B.
\(x = 4\)
-
C.
\(x = - 3\)
-
D.
\(x = 3\)
Cho hàm số \(f\left( x \right) = \frac{{ - 3}}{4}x.\) Để f(x) nhận giá trị dương thì
-
A.
\(x > 0\)
-
B.
\(x < 0\)
-
C.
\(x = 0\)
-
D.
Không xác định được
Cho hàm số: \(f\left( x \right) = \frac{3}{4}{x^2} + 5.\) Khẳng định nào sau đây là đúng?
-
A.
\(f\left( x \right)\) nhận giá trị dương với mọi giá trị của x
-
B.
\(f\left( x \right)\) nhận giá trị âm với mọi giá trị của x
-
C.
\(f\left( x \right) = 0\) với mọi giá trị của x
-
D.
Cả A, B, C đều sai.
Cho hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ge \frac{{ - 1}}{2}\\ - 2x - 1\;khi\;x < \frac{{ - 1}}{2}\end{array} \right.\). Chọn khẳng định đúng.
-
A.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 6\)
-
B.
\(f\left( { - 1} \right) + f\left( 2 \right) = 6\)
-
C.
\(f\left( { - 1} \right) + f\left( 2 \right) = 1\)
-
D.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 4\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ thuận với x theo hệ số tỷ lệ \(\frac{1}{2}.\) Khẳng định nào dưới đây đúng?
-
A.
\(f\left( 1 \right) + \frac{1}{2} = - 1\)
-
B.
\(f\left( 1 \right) + \frac{1}{2} = 0\)
-
C.
\(f\left( 1 \right) + \frac{1}{2} = 2\)
-
D.
\(f\left( 1 \right) + \frac{1}{2} = 1\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ nghịch với x theo hệ số \(a = 12.\)
Khẳng định nào sau đây đúng?
-
A.
\(f\left( { - x} \right) = f\left( x \right)\)
-
B.
\(f\left( { - x} \right) = - f\left( x \right)\)
-
C.
\(f\left( { - x} \right) = 2f\left( x \right)\)
-
D.
\(f\left( { - x} \right) = - 2f\left( x \right)\)
Cho hàm số \(y = f\left( x \right) = kx\) (k là hằng số, \(k \ne 0\)). Chọn đáp án đúng.
-
A.
\(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
B.
\(f\left( {{x_1} + {x_2}} \right) > f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
C.
\(f\left( {{x_1} + {x_2}} \right) < f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
D.
\(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\)
Hàm số f(x) được cho bởi bảng sau
| x | 2 | 3 | 4 |
| f(x) | -4 | -6 | -8 |
Hàm số trên được cho bởi công thức:
-
A.
\(f\left( x \right) = - x\)
-
B.
\(f\left( x \right) = 2x\)
-
C.
\(f\left( x \right) = - 2x\)
-
D.
\(f\left( x \right) = \frac{{ - 1}}{2}x\)
Cho hàm số \(f\left( x \right) = a{x^2} + ax + 1.\) Biết rằng \(f\left( 1 \right) = 3\), khi đó giá trị của a là:
-
A.
\(a = 1\)
-
B.
\(a = 2\)
-
C.
\(a = - 1\)
-
D.
\(a = - 2\)
Có bao nhiêu giá trị của a để giá trị hàm số \(f\left( x \right) = {x^2} - 2ax + {a^2} + 1\) luôn lớn hơn 0?
-
A.
0 giá trị
-
B.
1 giá trị
-
C.
2 giá trị
-
D.
Vô số giá trị
Giầy cỡ 36 ứng với khoảng cách d từ gót chân đến mũi ngón chân là 23cm. Khi khoảng cách d tăng (hay giảm) \(\frac{2}{3}cm\) thì cỡ giầy tăng (hay giảm) 1 số. Ta có bảng:
| d(cm) | 19 | 23 | |
| Cỡ giầy | 33 | 36 |
Hãy chọn bảng đúng trong các bảng dưới đây:
-
A.
d(cm) 19 21 23 Cỡ giầy 32 33 36 -
B.
d(cm) 19 22 23 Cỡ giầy 29 33 36 -
C.
d(cm) 19 20 23 Cỡ giầy 31 33 36 -
D.
d(cm) 19 21 23 Cỡ giầy 30 33 36
Cho hàm số \(y = f\left( x \right)\) được xác định bởi tương ứng giữa số que diêm (f(x)) và số hình vuông tạo thành (x) được nêu trong bảng sau:

Tính \(f\left( {12} \right)\)
-
A.
\(f\left( {12} \right) = 32\)
-
B.
\(f\left( {12} \right) = 33\)
-
C.
\(f\left( {12} \right) = 34\)
-
D.
\(f\left( {12} \right) = 37\)
Cho hai hàm số: \(f\left( x \right) = - 6{x^2} + 12x - 7,g\left( x \right) = 3{x^2} + 6x + 4\)
Khẳng định nào sau đây là đúng?
-
A.
\(f\left( x \right) > 0,g\left( x \right) > 0\) với mọi x
-
B.
\(f\left( x \right) < 0,g\left( x \right) > 0\) với mọi x
-
C.
\(f\left( x \right) = 0,g\left( x \right) > 0\) với mọi x
-
D.
\(f\left( x \right) > 0,g\left( x \right) = 0\) với mọi x
Chọn khẳng định đúng.
-
A.
Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó, ta có hệ trục tọa độ Oxy.
-
B.
Trên mặt phẳng, vẽ hai trục Ox, Oy cắt nhau tại O. Khi đó, ta có hệ trục tọa độ Oxy.
-
C.
Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau. Khi đó, ta có hệ trục tọa độ Oxy.
-
D.
Cả A, B, C đều sai
Cho điểm M(a; b) trong mặt phẳng tọa độ Oxy, khi đó:
-
A.
a là tung độ, b là hoành độ của điểm M
-
B.
\( - a\) là tung độ, b là hoành độ của điểm M
-
C.
\( - a\) là hoành độ, b là tung độ của điểm M
-
D.
a là hoành độ, b là tung độ của điểm M
Điểm thuộc trục hoành thì có tung độ bằng:
-
A.
2
-
B.
1
-
C.
0
-
D.
\( - 1\)
Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M có tọa độ:
-
A.
\(M\left( {x;f\left( x \right)} \right)\)
-
B.
\(M\left( {f\left( x \right);x} \right)\)
-
C.
\(M\left( {f\left( { - x} \right);x} \right)\)
-
D.
\(M\left( {x;f\left( { - x} \right)} \right)\)
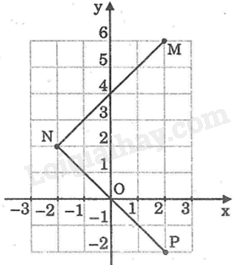
-
A.
\(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2\)
-
B.
\(f\left( 1 \right) = - 2;f\left( 2 \right) = 1\)
-
C.
\(f\left( { - 2} \right) = - 1;f\left( 1 \right) = - 2\)
-
D.
Cả A, B, C đều sai.
Điểm A(1;3) không thuộc đồ thị hàm số:
-
A.
\(y = x + 2\)
-
B.
\(y = 2x + 1\)
-
C.
\(y = 4 - x\)
-
D.
\(y = {x^2}\)
-
A.
(1; 2)
-
B.
(1; 3)
-
C.
(1; 1)
-
D.
(2; 1)
Trong mặt phẳng tọa độ Oxy cho điểm A nằm trên trục tung và có tung độ là 2. Điểm A’ đối xứng với điểm A qua gốc tọa độ O có tọa độ là:
-
A.
A’(-2; 0)
-
B.
A’(0; 2)
-
C.
A’(0; 2)
-
D.
A’(0; -2)
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB như hình vẽ dưới đây. Hàm số \(y = f\left( x \right)\) được cho bởi công thức nào?
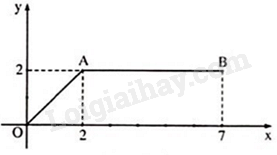
-
A.
\(y = x\)
-
B.
\(y = 2\)
-
C.
\(y = \left\{ \begin{array}{l}x\;\;khi\;\;0 \le x \le 2\\2\;\;khi\;\;2 < x \le 7\end{array} \right.\)
-
D.
\(y = \left\{ \begin{array}{l}x\;\;khi\;\;x \le 2\\2\;\;khi\;\;x > 2\end{array} \right.\)
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB, và đồ thị hàm số \(y = g\left( x \right) = \frac{1}{3}x\) như hình vẽ dưới đây:
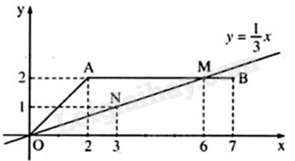
Có bao nhiêu giá trị của x để \(f\left( x \right) = g\left( x \right)\)
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Trong mặt phẳng tọa độ cho các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right).\) Trong các đoạn thẳng MP, PQ, NQ, MN, số đoạn thẳng song song với trục hoành là:
-
A.
1
-
B.
2
-
C.
3
-
D.
4
-
A.
Q(6; 4)
-
B.
Q(4; 2)
-
C.
Q(2; 6)
-
D.
Q(6; 2)
Cho đồ thị hàm số \(y = - 3{x^2} + 1\) và điểm C thuộc đồ thị đó. Nếu tung độ của điểm C là 1 thì tọa độ của điểm C là:
-
A.
\(C\left( { - 1;1} \right)\)
-
B.
\(C\left( { - 1; - 1} \right)\)
-
C.
\(C\left( {0;1} \right)\)
-
D.
\(C\left( {1;0} \right)\)
Cho đồ thị hàm số \(y = 6x.\) Điểm A thuộc đồ thị hàm số đó. Biết rằng điểm A có hoành độ bằng 2. Khi đó, tọa độ của điểm A là:
-
A.
\(A\left( {12;2} \right)\)
-
B.
\(A\left( {2;\frac{1}{3}} \right)\)
-
C.
\(A\left( {2;0} \right)\)
-
D.
\(A\left( {2;12} \right)\)
Cho hàm số \(y = \left( {2m - 1} \right){x^2}.\) Biết rằng đồ thị hàm số trên đi qua điểm A(1; 1). Khi đó,
-
A.
\(m = 2\)
-
B.
\(m = 0\)
-
C.
\(m = 1\)
-
D.
\(m = - 1\)
: Cho hệ trục tọa độ Oxy, diện tích của hình chữ nhật giới hạn bởi hai trục tọa độ và hai đường thẳng chứa tất cả các điểm có hoành độ bằng 3 và tất cả các điểm có tung độ bằng 2 là:
-
A.
4đvdt
-
B.
5đvdt
-
C.
6đvdt
-
D.
7đvdt
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(1; 4), B(-3; -4), C(1; 0). Khi đó, diện tích tam giác ABC là:
-
A.
4đvdt
-
B.
8đvdt
-
C.
6đvdt
-
D.
12đvdt
Lời giải và đáp án
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y.
Chọn đáp án đúng
-
A.
y được gọi là hàm số của biến số x
-
B.
x được gọi là hàm số của biến số y
-
C.
Cả A và B đều đúng
-
D.
Cả A và B đều sai
Đáp án : A
-
A.
y là hàm số của biến số x
-
B.
x là hàm số của biến số y
-
C.
y tỉ lệ thuận với x
-
D.
y tỉ lệ nghịch với x
Đáp án : A
Tuy nhiên, x không phải là hàm số của biến số y, vì với y = 2, ta có 2 giá trị x tương ứng x = -5 và x = 6.
Trong các công thức dưới đây, công thức nào thể hiện y không phải là hàm số của x?
-
A.
\(y = x + 1\)
-
B.
\(y = \frac{1}{2}x\)
-
C.
\(y = {x^2}\)
-
D.
\({y^2} = x\)
Đáp án : D
Với \(x = 4\) thì \({y^2} = 4\) nên \(y = 2\) hoặc \(y = - 2\)
Ta thấy với mỗi giá trị của x có tương ứng 2 giá trị của y nên \({y^2} = x\) không phải là hàm số của x.
Các công thức còn lại ta đều thấy với mỗi giá trị của x có duy nhất một giá trị tương ứng của y nên y là hàm số của x.
Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y...f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
Đáp án đúng điền vào “…”.
-
A.
\( > \)
-
B.
\( < \)
-
C.
\( = \)
-
D.
\( \ne \)
Đáp án : C
Nhiệt độ N của một nhà máy ấp trứng vịt được cài đặt luôn bằng 37oC không thay đổi theo thời gian t. Khi đó, công thức xác định hàm số N(t) của nhiệt độ theo thời gian là:
-
A.
\(N\left( t \right) = 37\)
-
B.
\(N\left( t \right) > 37\)
-
C.
\(N\left( t \right) < 37\)
-
D.
\(N\left( t \right) \ge 37\)
Đáp án : A
Một hàm số được cho bởi công thức \(f\left( x \right) = \frac{{ - 1}}{2}x + 5.\) Khẳng định nào sau đây là đúng?
-
A.
\(f\left( 1 \right) > f\left( 2 \right)\)
-
B.
\(f\left( 1 \right) = f\left( 2 \right)\)
-
C.
\(f\left( 1 \right) < f\left( 2 \right)\)
-
D.
\(f\left( 1 \right) \le f\left( 2 \right)\)
Đáp án : A
Ta có: \(f\left( 1 \right) = \frac{{ - 1}}{2}.1 + 5 = \frac{9}{2};f\left( 2 \right) = \frac{{ - 1}}{2}.2 + 5 = 4\)
Vì \(\frac{9}{2} > 4\) nên \(f\left( 1 \right) > f\left( 2 \right)\)
Một hình lập phương có độ dài cạnh là x (cm) và thể tích là \(V\left( {c{m^3}} \right)\).
Chọn khẳng định đúng.
-
A.
\(V = {x^2},\) V là hàm số của biến số x.
-
B.
\(V = {x^2},\) V là không hàm số của biến số x.
-
C.
\(V = {x^3},\) V là hàm số của biến số x.
-
D.
\(V = {x^3},\) V không là hàm số của biến số x.
Đáp án : C
Thể tích của hình lập phương là: \(V = {x^3}\)
Vì mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của V nên V là hàm số của biến số x.
Nhà bác học Galileo Galilei là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y(m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}.\) Quãng đường mà vật đó chuyển động được sau 4 giây là:
-
A.
60m
-
B.
70m
-
C.
80m
-
D.
90m
Đáp án : C
Xét hàm số \(y = 5{x^2}.\)
Quãng đường vật chuyển động được sau 4 giây ứng với \(x = 4\)
Do đó, \(y = {5.4^2} = 5.16 = 80\left( m \right)\)
Cho hàm số \(f\left( x \right) = 3{x^4} - 3{x^2} - 1.\) So sánh f(x) và f(-x)
-
A.
\(f\left( x \right) < f\left( { - x} \right)\)
-
B.
\(f\left( x \right) = f\left( { - x} \right)\)
-
C.
\(f\left( x \right) > f\left( { - x} \right)\)
-
D.
Không so sánh được f(x) và f(-x)
Đáp án : B
Ta có: \(f\left( { - x} \right) = 3{\left( { - x} \right)^4} - 3{\left( { - x} \right)^2} - 1 = 3{x^4} - 3{x^2} - 1\)
Mà \(f\left( x \right) = 3{x^4} - 3{x^2} - 1.\)
Do đó, \(f\left( x \right) = f\left( { - x} \right)\)
Cho hàm số \(f\left( x \right) = 30x + 100.\) Để \(f\left( x \right) = 190\) thì giá trị của x là:
-
A.
\(x = - 4\)
-
B.
\(x = 4\)
-
C.
\(x = - 3\)
-
D.
\(x = 3\)
Đáp án : D
Với \(f\left( x \right) = 190\) thì ta có: \(190 = 30x + 100\)
\(30x = 90\)
\(x = 3\)
Cho hàm số \(f\left( x \right) = \frac{{ - 3}}{4}x.\) Để f(x) nhận giá trị dương thì
-
A.
\(x > 0\)
-
B.
\(x < 0\)
-
C.
\(x = 0\)
-
D.
Không xác định được
Đáp án : B
Để f(x) nhận giá trị dương thì \(f\left( x \right) > 0\) tức là \(\frac{{ - 3}}{4}.x > 0\)
Mà \(\frac{{ - 3}}{4} < 0\) nên \(x < 0\)
Cho hàm số: \(f\left( x \right) = \frac{3}{4}{x^2} + 5.\) Khẳng định nào sau đây là đúng?
-
A.
\(f\left( x \right)\) nhận giá trị dương với mọi giá trị của x
-
B.
\(f\left( x \right)\) nhận giá trị âm với mọi giá trị của x
-
C.
\(f\left( x \right) = 0\) với mọi giá trị của x
-
D.
Cả A, B, C đều sai.
Đáp án : A
Vì \({x^2} \ge 0\) với mọi số thực x nên \(\frac{3}{4}{x^2} \ge 0\) với mọi số thực x.
Do đó, \(\frac{3}{4}{x^2} + 5 > 0\) với mọi số thực x.
Suy ra: \(f\left( x \right) > 0\) với mọi số thực x.
Vậy \(f\left( x \right)\) nhận giá trị dương với mọi giá trị của x.
Cho hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ge \frac{{ - 1}}{2}\\ - 2x - 1\;khi\;x < \frac{{ - 1}}{2}\end{array} \right.\). Chọn khẳng định đúng.
-
A.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 6\)
-
B.
\(f\left( { - 1} \right) + f\left( 2 \right) = 6\)
-
C.
\(f\left( { - 1} \right) + f\left( 2 \right) = 1\)
-
D.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 4\)
Đáp án : B
Với \(x = - 1 < \frac{{ - 1}}{2}\) thì ta có: \(f\left( { - 1} \right) = - 2\left( { - 1} \right) - 1 = 2 - 1 = 1\)
Với \(x = 2 > \frac{{ - 1}}{2}\) thì ta có: \(f\left( 2 \right) = 2.2 + 1 = 4 + 1 = 5\)
Do đó, \(f\left( { - 1} \right) + f\left( 2 \right) = 1 + 5 = 6\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ thuận với x theo hệ số tỷ lệ \(\frac{1}{2}.\) Khẳng định nào dưới đây đúng?
-
A.
\(f\left( 1 \right) + \frac{1}{2} = - 1\)
-
B.
\(f\left( 1 \right) + \frac{1}{2} = 0\)
-
C.
\(f\left( 1 \right) + \frac{1}{2} = 2\)
-
D.
\(f\left( 1 \right) + \frac{1}{2} = 1\)
Đáp án : D
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Vì y tỉ lệ thuận với x theo hệ số tỷ lệ \(\frac{1}{2}\) nên \(y = f\left( x \right) = \frac{1}{2}x\)
Ta có: \(f\left( 1 \right) = \frac{1}{2}.1 = \frac{1}{2}\) nên \(f\left( 1 \right) + \frac{1}{2} = 1\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ nghịch với x theo hệ số \(a = 12.\)
Khẳng định nào sau đây đúng?
-
A.
\(f\left( { - x} \right) = f\left( x \right)\)
-
B.
\(f\left( { - x} \right) = - f\left( x \right)\)
-
C.
\(f\left( { - x} \right) = 2f\left( x \right)\)
-
D.
\(f\left( { - x} \right) = - 2f\left( x \right)\)
Đáp án : B
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Vì y tỉ lệ nghịch với x theo hệ số \(a = 12\) nên \(xy = 12,\) do đó \(y = f\left( x \right) = \frac{{12}}{x}\)
Ta có: \(f\left( { - x} \right) = \frac{{12}}{{ - x}} = - \frac{{12}}{x} = - f\left( x \right)\)
Vậy \(f\left( { - x} \right) = - f\left( x \right)\)
Cho hàm số \(y = f\left( x \right) = kx\) (k là hằng số, \(k \ne 0\)). Chọn đáp án đúng.
-
A.
\(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
B.
\(f\left( {{x_1} + {x_2}} \right) > f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
C.
\(f\left( {{x_1} + {x_2}} \right) < f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
-
D.
\(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\)
Đáp án : A
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Ta có: \(f\left( {{x_1}} \right) = k{x_1},f\left( {{x_2}} \right) = k{x_2},f\left( {{x_1}} \right) + f\left( {{x_2}} \right) = k{x_1} + k{x_2} = k\left( {{x_1} + {x_2}} \right)\)
\(f\left( {{x_1} + {x_2}} \right) = k\left( {{x_1} + {x_2}} \right)\)
Do đó, \(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) + f\left( {{x_2}} \right)\)
Hàm số f(x) được cho bởi bảng sau
| x | 2 | 3 | 4 |
| f(x) | -4 | -6 | -8 |
Hàm số trên được cho bởi công thức:
-
A.
\(f\left( x \right) = - x\)
-
B.
\(f\left( x \right) = 2x\)
-
C.
\(f\left( x \right) = - 2x\)
-
D.
\(f\left( x \right) = \frac{{ - 1}}{2}x\)
Đáp án : C
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Với \(x = 2\) ta có: \(f\left( 2 \right) = - 4 = - 2.2\)
Với \(x = 3\) ta có: \(f\left( 3 \right) = - 6 = - 2.3\)
Với \(x = 4\) ta có: \(f\left( 4 \right) = - 8 = - 2.4\)
Do đó, \(f\left( x \right) = - 2x\)
Cho hàm số \(f\left( x \right) = a{x^2} + ax + 1.\) Biết rằng \(f\left( 1 \right) = 3\), khi đó giá trị của a là:
-
A.
\(a = 1\)
-
B.
\(a = 2\)
-
C.
\(a = - 1\)
-
D.
\(a = - 2\)
Đáp án : A
Ta có: \(f\left( 1 \right) = a{.1^2} + a.1 + 1 = 2a + 1\)
Mà \(f\left( 1 \right) = 3\) nên \(2a + 1 = 3\)
\(2a = 2\)
\(a = 1\)
Có bao nhiêu giá trị của a để giá trị hàm số \(f\left( x \right) = {x^2} - 2ax + {a^2} + 1\) luôn lớn hơn 0?
-
A.
0 giá trị
-
B.
1 giá trị
-
C.
2 giá trị
-
D.
Vô số giá trị
Đáp án : D
Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
Ta có: \(f\left( x \right) = {x^2} - 2ax + {a^2} + 1 = {\left( {x - a} \right)^2} + 1\)
Vì \({\left( {x - a} \right)^2} \ge 0\) với mọi giá trị của a, x nên \({\left( {x - a} \right)^2} + 1 > 0\) với mọi giá trị của x, a.
Vậy có vô số giá trị của a để giá trị hàm số \(f\left( x \right) = {x^2} - 2ax + {a^2} + 1\) luôn lớn hơn 0.
Giầy cỡ 36 ứng với khoảng cách d từ gót chân đến mũi ngón chân là 23cm. Khi khoảng cách d tăng (hay giảm) \(\frac{2}{3}cm\) thì cỡ giầy tăng (hay giảm) 1 số. Ta có bảng:
| d(cm) | 19 | 23 | |
| Cỡ giầy | 33 | 36 |
Hãy chọn bảng đúng trong các bảng dưới đây:
-
A.
d(cm) 19 21 23 Cỡ giầy 32 33 36 -
B.
d(cm) 19 22 23 Cỡ giầy 29 33 36 -
C.
d(cm) 19 20 23 Cỡ giầy 31 33 36 -
D.
d(cm) 19 21 23 Cỡ giầy 30 33 36
Đáp án : D
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Với \(d = 19\) ta có: \(23 - 19 = 4 = \frac{2}{3}.6\left( {cm} \right)\), tức là từ \(d = 23\) xuống \(d = 19\) thì khoảng cách d giảm đi \(6.\frac{2}{3}cm\), do đó, cỡ giày giảm đi 6 số. Vậy \(d = 19\) ứng với cỡ giày: \(36 - 6 = 30\)
Với giày cỡ 33 thì từ cỡ giày 36 xuống cỡ giày 33 giảm đi \(3.\frac{2}{3} = 2\left( {cm} \right)\)
Do đó, với cỡ giày thứ 33 thì khoảng cách d là: \(23 - 2 = 21\left( {cm} \right)\)
Vậy ta có bảng đúng là:
| d(cm) | 19 | 21 | 23 |
| Cỡ giầy | 30 | 33 | 36 |
Cho hàm số \(y = f\left( x \right)\) được xác định bởi tương ứng giữa số que diêm (f(x)) và số hình vuông tạo thành (x) được nêu trong bảng sau:

Tính \(f\left( {12} \right)\)
-
A.
\(f\left( {12} \right) = 32\)
-
B.
\(f\left( {12} \right) = 33\)
-
C.
\(f\left( {12} \right) = 34\)
-
D.
\(f\left( {12} \right) = 37\)
Đáp án : D
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Với \(x = 1\) ta có: \(f\left( 1 \right) = 4 = 3.1 + 1\)
Với \(x = 2\) ta có: \(f\left( 2 \right) = 7 = 3.2 + 1\)
Với \(x = 3\) ta có: \(f\left( 3 \right) = 10 = 3.3 + 1\)
Do đó, công thức của hàm số là: \(f\left( x \right) = 3x + 1\)
Vậy \(f\left( {12} \right) = 3.12 + 1 = 37\)
Cho hai hàm số: \(f\left( x \right) = - 6{x^2} + 12x - 7,g\left( x \right) = 3{x^2} + 6x + 4\)
Khẳng định nào sau đây là đúng?
-
A.
\(f\left( x \right) > 0,g\left( x \right) > 0\) với mọi x
-
B.
\(f\left( x \right) < 0,g\left( x \right) > 0\) với mọi x
-
C.
\(f\left( x \right) = 0,g\left( x \right) > 0\) với mọi x
-
D.
\(f\left( x \right) > 0,g\left( x \right) = 0\) với mọi x
Đáp án : B
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Ta có: \(f\left( x \right) = - 6{x^2} + 12x - 7 = - 6{x^2} + 12x - 6 - 1 = - 6\left( {{x^2} - 2x + 1} \right) - 1 = - 6{\left( {x - 1} \right)^2} - 1 < 0\) với mọi x.
\(g\left( x \right) = 3{x^2} + 6x + 4 = 3{x^2} + 6x + 3 + 1 = 3\left( {{x^2} + 2x + 1} \right) + 1 = 3{\left( {x + 1} \right)^2} + 1 > 0\) với mọi x.
Chọn khẳng định đúng.
-
A.
Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó, ta có hệ trục tọa độ Oxy.
-
B.
Trên mặt phẳng, vẽ hai trục Ox, Oy cắt nhau tại O. Khi đó, ta có hệ trục tọa độ Oxy.
-
C.
Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau. Khi đó, ta có hệ trục tọa độ Oxy.
-
D.
Cả A, B, C đều sai
Đáp án : A
Cho điểm M(a; b) trong mặt phẳng tọa độ Oxy, khi đó:
-
A.
a là tung độ, b là hoành độ của điểm M
-
B.
\( - a\) là tung độ, b là hoành độ của điểm M
-
C.
\( - a\) là hoành độ, b là tung độ của điểm M
-
D.
a là hoành độ, b là tung độ của điểm M
Đáp án : D
Điểm thuộc trục hoành thì có tung độ bằng:
-
A.
2
-
B.
1
-
C.
0
-
D.
\( - 1\)
Đáp án : C
Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M có tọa độ:
-
A.
\(M\left( {x;f\left( x \right)} \right)\)
-
B.
\(M\left( {f\left( x \right);x} \right)\)
-
C.
\(M\left( {f\left( { - x} \right);x} \right)\)
-
D.
\(M\left( {x;f\left( { - x} \right)} \right)\)
Đáp án : A
-
A.
\(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2\)
-
B.
\(f\left( 1 \right) = - 2;f\left( 2 \right) = 1\)
-
C.
\(f\left( { - 2} \right) = - 1;f\left( 1 \right) = - 2\)
-
D.
Cả A, B, C đều sai.
Đáp án : A
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
+ Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M.
Từ hình vẽ ta thấy B(-2;1) và điểm A(1;2) thuộc đồ thị hàm số.
Do đó, \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2\)
Điểm A(1;3) không thuộc đồ thị hàm số:
-
A.
\(y = x + 2\)
-
B.
\(y = 2x + 1\)
-
C.
\(y = 4 - x\)
-
D.
\(y = {x^2}\)
Đáp án : D
Ta thấy: \(3 \ne {1^2}\) nên điểm A(1;3) không thuộc đồ thị hàm số \(y = {x^2}\)
-
A.
(1; 2)
-
B.
(1; 3)
-
C.
(1; 1)
-
D.
(2; 1)
Đáp án : C
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
+ Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M.
Nhìn vào đồ thị trong hình vẽ ta thấy, \(x = 1\) thì \(y = 1\)
Vậy điểm có tọa độ (1; 1) thuộc đồ thị hàm số.
Trong mặt phẳng tọa độ Oxy cho điểm A nằm trên trục tung và có tung độ là 2. Điểm A’ đối xứng với điểm A qua gốc tọa độ O có tọa độ là:
-
A.
A’(-2; 0)
-
B.
A’(0; 2)
-
C.
A’(0; 2)
-
D.
A’(0; -2)
Đáp án : D
Vì điểm A nằm trên trục tung và có tung độ bằng 2 nên A(0; 2)
Điểm A’ đối xứng với điểm A qua gốc tọa độ O nên O là trung điểm của đoạn thẳng AA’.
Do đó, A’ thuộc trục tung và có tung độ là \( - 2\)
Vậy A’(0; -2)
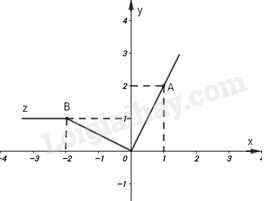
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB như hình vẽ dưới đây. Hàm số \(y = f\left( x \right)\) được cho bởi công thức nào?

-
A.
\(y = x\)
-
B.
\(y = 2\)
-
C.
\(y = \left\{ \begin{array}{l}x\;\;khi\;\;0 \le x \le 2\\2\;\;khi\;\;2 < x \le 7\end{array} \right.\)
-
D.
\(y = \left\{ \begin{array}{l}x\;\;khi\;\;x \le 2\\2\;\;khi\;\;x > 2\end{array} \right.\)
Đáp án : C
Nhìn vào đồ thị ta thấy:
Với \(2 < x \le 7\) ta thấy đồ thị hàm số là đường thẳng \(y = 2\)
Với \(0 \le x \le 2\) ta thấy đồ thị hàm số là đường thẳng \(y = x\)
Vậy \(y = \left\{ \begin{array}{l}x\;\;khi\;\;0 \le x \le 2\\2\;\;khi\;\;2 < x \le 7\end{array} \right.\)
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB, và đồ thị hàm số \(y = g\left( x \right) = \frac{1}{3}x\) như hình vẽ dưới đây:

Có bao nhiêu giá trị của x để \(f\left( x \right) = g\left( x \right)\)
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Đáp án : C
Đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại điểm O(0;0) và M(6;2)
Với \(x = 0\) thì \(f\left( x \right) = g\left( x \right) = 0\)
Với \(x = 6\) thì \(f\left( x \right) = g\left( x \right) = 2\)
Do đó, có 2 giá trị của x để \(f\left( x \right) = g\left( x \right)\)
Trong mặt phẳng tọa độ cho các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right).\) Trong các đoạn thẳng MP, PQ, NQ, MN, số đoạn thẳng song song với trục hoành là:
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
Biểu diễn các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right)\) trên mặt phẳng tọa độ
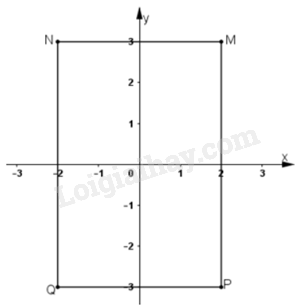
Nhìn vào đồ thị ta thấy đoạn thẳng song song với trục hoành là MN và PQ.
-
A.
Q(6; 4)
-
B.
Q(4; 2)
-
C.
Q(2; 6)
-
D.
Q(6; 2)
Đáp án : D
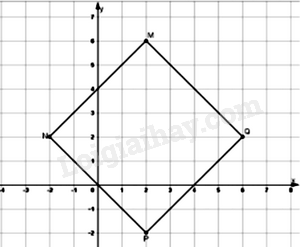
Điểm P cách điểm N là 4 ô chéo thì điểm Q cũng cách điểm M 4 ô chéo
Điểm N cách trục hoành 2 ô vuông thì điểm Q cách trục hoành 2 ô vuông.
Do đó, điểm Q(6; 2)
Cho đồ thị hàm số \(y = - 3{x^2} + 1\) và điểm C thuộc đồ thị đó. Nếu tung độ của điểm C là 1 thì tọa độ của điểm C là:
-
A.
\(C\left( { - 1;1} \right)\)
-
B.
\(C\left( { - 1; - 1} \right)\)
-
C.
\(C\left( {0;1} \right)\)
-
D.
\(C\left( {1;0} \right)\)
Đáp án : C
Vì tung độ của điểm C là 1 nên \(y = 1\). Thay \(y = 1\) vào \(y = - 3{x^2} + 1\) ta có:
\(1 = - 3{x^2} + 1\)
\(0 = - 3{x^2}\)
\(x = 0\)
Vậy \(C\left( {0;1} \right)\)
Cho đồ thị hàm số \(y = 6x.\) Điểm A thuộc đồ thị hàm số đó. Biết rằng điểm A có hoành độ bằng 2. Khi đó, tọa độ của điểm A là:
-
A.
\(A\left( {12;2} \right)\)
-
B.
\(A\left( {2;\frac{1}{3}} \right)\)
-
C.
\(A\left( {2;0} \right)\)
-
D.
\(A\left( {2;12} \right)\)
Đáp án : D
Điểm A có hoành độ bằng 2 nên \(x = 2.\) Thay \(x = 2\) vào \(y = 6x\) ta có: \(y = 2.6 = 12\)
Vậy A(2; 12)
Cho hàm số \(y = \left( {2m - 1} \right){x^2}.\) Biết rằng đồ thị hàm số trên đi qua điểm A(1; 1). Khi đó,
-
A.
\(m = 2\)
-
B.
\(m = 0\)
-
C.
\(m = 1\)
-
D.
\(m = - 1\)
Đáp án : C
Vì đồ thị hàm số đã cho đi qua A(1; 1) nên \(x = 1;y = 1.\) Thay vào hàm số ta có:
\(1 = \left( {2m - 1} \right){.1^2}\)
\(1 = 2m - 1\)
\(2m = 2\)
\(m = 1\)
Vậy với \(m = 1\) thì thỏa mãn yêu cầu bài toán
: Cho hệ trục tọa độ Oxy, diện tích của hình chữ nhật giới hạn bởi hai trục tọa độ và hai đường thẳng chứa tất cả các điểm có hoành độ bằng 3 và tất cả các điểm có tung độ bằng 2 là:
-
A.
4đvdt
-
B.
5đvdt
-
C.
6đvdt
-
D.
7đvdt
Đáp án : C
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Các điểm có hoành độ bằng 3 nằm trên đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng 3.
Các điểm có tung độ bằng 2 nằm trên đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 2.
Do đó, ta có đồ thị hàm số:
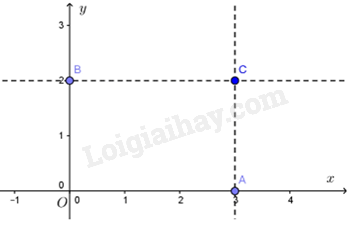
Gọi tên các giao điểm như hình vẽ, ta được hình chữ nhật OBCA.
Do đó, diện tích hình chữ nhật OBCA là: \({S_{OBCA}} = OA.OB = 3.2 = 6\) (đvdt)
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(1; 4), B(-3; -4), C(1; 0). Khi đó, diện tích tam giác ABC là:
-
A.
4đvdt
-
B.
8đvdt
-
C.
6đvdt
-
D.
12đvdt
Đáp án : B
Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ Oxy ta được:
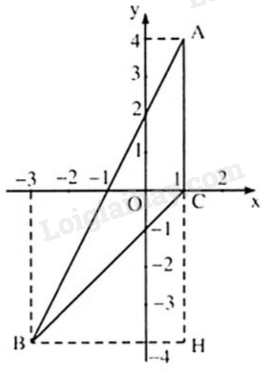
Kẻ BH vuông góc với AC, khi đó, BH là đường cao trong tam giác ABC.
Diện tích tam giác ABC là:
\({S_{ABC}} = \frac{1}{2}BH.AC = \frac{1}{2}.4.4 = 8\) (đvdt)
Luyện tập và củng cố kiến thức Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 29: Hệ số góc của đường thẳng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 26: Giải bài toán bằng cách lập phương trình Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 25: Phương trình bậc nhất một ẩn Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 39: Hình chóp tứ giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 38: Hình chóp tam giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 37: Hình đồng dạng Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 35: Định lí Pythagore và ứng dụng Toán 8 Kết nối tri thức










Danh sách bình luận