Giầy cỡ 36 ứng với khoảng cách d từ gót chân đến mũi ngón chân là 23cm. Khi khoảng cách d tăng (hay giảm) \(\frac{2}{3}cm\) thì cỡ giầy tăng (hay giảm) 1 số. Ta có bảng:
| d(cm) | 19 | 23 | |
| Cỡ giầy | 33 | 36 |
Hãy chọn bảng đúng trong các bảng dưới đây:
-
A.
d(cm) 19 21 23 Cỡ giầy 32 33 36 -
B.
d(cm) 19 22 23 Cỡ giầy 29 33 36 -
C.
d(cm) 19 20 23 Cỡ giầy 31 33 36 -
D.
d(cm) 19 21 23 Cỡ giầy 30 33 36
+ Sử dụng giá trị của hàm số: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
+ Sử dụng khái niệm hàm số: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.
Với \(d = 19\) ta có: \(23 - 19 = 4 = \frac{2}{3}.6\left( {cm} \right)\), tức là từ \(d = 23\) xuống \(d = 19\) thì khoảng cách d giảm đi \(6.\frac{2}{3}cm\), do đó, cỡ giày giảm đi 6 số. Vậy \(d = 19\) ứng với cỡ giày: \(36 - 6 = 30\)
Với giày cỡ 33 thì từ cỡ giày 36 xuống cỡ giày 33 giảm đi \(3.\frac{2}{3} = 2\left( {cm} \right)\)
Do đó, với cỡ giày thứ 33 thì khoảng cách d là: \(23 - 2 = 21\left( {cm} \right)\)
Vậy ta có bảng đúng là:
| d(cm) | 19 | 21 | 23 |
| Cỡ giầy | 30 | 33 | 36 |
Đáp án : D

Các bài tập cùng chuyên đề
Cho hàm số \(y = f\left( x \right)\) được xác định bởi tương ứng giữa số que diêm (f(x)) và số hình vuông tạo thành (x) được nêu trong bảng sau:

Tính \(f\left( {12} \right)\)
-
A.
\(f\left( {12} \right) = 32\)
-
B.
\(f\left( {12} \right) = 33\)
-
C.
\(f\left( {12} \right) = 34\)
-
D.
\(f\left( {12} \right) = 37\)
Có bao nhiêu giá trị của a để giá trị hàm số \(f\left( x \right) = {x^2} - 2ax + {a^2} + 1\) luôn lớn hơn 0?
-
A.
0 giá trị
-
B.
1 giá trị
-
C.
2 giá trị
-
D.
Vô số giá trị
Cho hàm số \(f\left( x \right) = a{x^2} + ax + 1.\) Biết rằng \(f\left( 1 \right) = 3\), khi đó giá trị của a là:
-
A.
\(a = 1\)
-
B.
\(a = 2\)
-
C.
\(a = - 1\)
-
D.
\(a = - 2\)
Cho hai hàm số \(f\left( x \right) = 2a{x^2} + 1,g\left( x \right) = 3x + 1.\) Biết rằng \(f\left( 1 \right) = g\left( 2 \right)\).
Chọn đáp án đúng.
-
A.
\(a = 1\)
-
B.
\(a = 2\)
-
C.
\(a = - 3\)
-
D.
\(a = 3\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ nghịch với x theo hệ số \(a = 12.\)
Khẳng định nào sau đây đúng?
-
A.
\(f\left( { - x} \right) = f\left( x \right)\)
-
B.
\(f\left( { - x} \right) = - f\left( x \right)\)
-
C.
\(f\left( { - x} \right) = 2f\left( x \right)\)
-
D.
\(f\left( { - x} \right) = - 2f\left( x \right)\)
Cho hàm số \(y = f\left( x \right)\), biết rằng y tỉ lệ thuận với x theo hệ số tỷ lệ \(\frac{1}{2}.\) Khẳng định nào dưới đây đúng?
-
A.
\(f\left( 1 \right) + \frac{1}{2} = - 1\)
-
B.
\(f\left( 1 \right) + \frac{1}{2} = 0\)
-
C.
\(f\left( 1 \right) + \frac{1}{2} = 2\)
-
D.
\(f\left( 1 \right) + \frac{1}{2} = 1\)
Cho hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ge \frac{{ - 1}}{2}\\ - 2x - 1\;khi\;x < \frac{{ - 1}}{2}\end{array} \right.\). Chọn khẳng định đúng.
-
A.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 6\)
-
B.
\(f\left( { - 1} \right) + f\left( 2 \right) = 6\)
-
C.
\(f\left( { - 1} \right) + f\left( 2 \right) = 1\)
-
D.
\(f\left( { - 1} \right) + f\left( 2 \right) = - 4\)
Cho hàm số \(f\left( x \right) = \frac{{ - 3}}{4}x.\) Để f(x) nhận giá trị dương thì
-
A.
\(x > 0\)
-
B.
\(x < 0\)
-
C.
\(x = 0\)
-
D.
Không xác định được
Cho hàm số \(f\left( x \right) = 30x + 100.\) Để \(f\left( x \right) = 190\) thì giá trị của x là:
-
A.
\(x = - 4\)
-
B.
\(x = 4\)
-
C.
\(x = - 3\)
-
D.
\(x = 3\)
Cho hàm số \(f\left( x \right) = 3{x^4} - 3{x^2} - 1.\) So sánh f(x) và f(-x)
-
A.
\(f\left( x \right) < f\left( { - x} \right)\)
-
B.
\(f\left( x \right) = f\left( { - x} \right)\)
-
C.
\(f\left( x \right) > f\left( { - x} \right)\)
-
D.
Không so sánh được f(x) và f(-x)
Nhà bác học Galileo Galilei là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y(m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}.\) Quãng đường mà vật đó chuyển động được sau 4 giây là:
-
A.
60m
-
B.
70m
-
C.
80m
-
D.
90m
Một hàm số được cho bởi công thức \(f\left( x \right) = \frac{{ - 1}}{2}x + 5.\) Khẳng định nào sau đây là đúng?
-
A.
\(f\left( 1 \right) > f\left( 2 \right)\)
-
B.
\(f\left( 1 \right) = f\left( 2 \right)\)
-
C.
\(f\left( 1 \right) < f\left( 2 \right)\)
-
D.
\(f\left( 1 \right) \le f\left( 2 \right)\)
Cho hàm số được cho bởi công thức \(y = f\left( x \right) = {x^3}.\) Tính \(f\left( { - 2} \right) + f\left( 2 \right)\)
-
A.
\(f\left( { - 2} \right) + f\left( 2 \right) = 16\)
-
B.
\(f\left( { - 2} \right) + f\left( 2 \right) = 0\)
-
C.
\(f\left( { - 2} \right) + f\left( 2 \right) = - 16\)
-
D.
\(f\left( { - 2} \right) + f\left( 2 \right) = - 8\)
Cho hàm số được cho bởi bảng sau:
| x | 1 | 2 | 3 | 4 |
| f(x) | 3 | 6 | 9 | 12 |
Chọn đáp án đúng
-
A.
\(f\left( 1 \right) - f\left( 3 \right) = - 2\)
-
B.
\(f\left( 1 \right) - f\left( 3 \right) = - 6\)
-
C.
\(f\left( 1 \right) - f\left( 3 \right) = - 9\)
-
D.
\(f\left( 1 \right) - f\left( 3 \right) = - 15\)
Nhiệt độ N của một nhà máy ấp trứng vịt được cài đặt luôn bằng 37oC không thay đổi theo thời gian t. Khi đó, công thức xác định hàm số N(t) của nhiệt độ theo thời gian là:
-
A.
\(N\left( t \right) = 37\)
-
B.
\(N\left( t \right) > 37\)
-
C.
\(N\left( t \right) < 37\)
-
D.
\(N\left( t \right) \ge 37\)
Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có: \(y...f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
Đáp án đúng điền vào “…”.
-
A.
\( > \)
-
B.
\( < \)
-
C.
\( = \)
-
D.
\( \ne \)
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(1; 4), B(-3; -4), C(1; 0). Khi đó, diện tích tam giác ABC là:
-
A.
4đvdt
-
B.
8đvdt
-
C.
6đvdt
-
D.
12đvdt
Ở lớp 6, ta đã biết rằng mỗi điểm trên bản đồ địa lí được xác định bởi một cặp gồm hai con số (tọa độ địa lí) là kinh độ và vĩ độ. Chẳng hạn, tọa độ địa lí của hồ Hoàn Kiếm ở Thủ đô Hà Nội là: (21o01’B; 105o51’Đ)
Trong toán học, cặp số để xác định vị trí của một điểm trên mặt phẳng được gọi là gì?
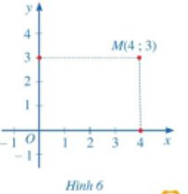
Cho điểm M trong mặt phẳng tọa độ Oxy (hình 6),
a) Hình chiếu của điểm M trên trục hoành Ox là điểm nào trên trục số Ox?
b) Hình chiếu của điểm M trên trục tung Oy là điểm nào trên trục số Oy?
Trong mặt phẳng tọa độ Oxy, hãy nêu cách xác định các điểm A(-1; 2); B(2; 2); C(2; 0); D(0; -2); E\(\left ( \frac{1}{2};-\frac{3}{4} \right) \).
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Điểm thuộc trục hoành có tung độ bằng 0.
b) Điểm thuộc trục hoành có hoành độ bằng 0.
c) Điểm thuộc trục tung có tung độ bằng 0.
d) Điểm thuộc trục tung có hoành độ bằng 0.
Xác định tọa độ điểm A trong mỗi trường hợp sau:
a) Hoành độ bằng -3 và tung độ bằng 5.
b) Hoành độ bằng -2 và nằm trên trục hoành.
c) Tung độ bằng -4 và nằm trên trục tung.
Trong mặt phẳng tọa độ Oxy, nêu cách xác định điểm A(-3; -5).
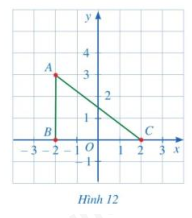
Cho tam giác ABC như hình 12
a) Xác định tọa độ các điểm A, B, C
b) Tam giác ABC có là tam giác vuông hay không?
c) Xác định tọa độ điểm D để tứ giác ABCD là hình chữ nhật
Nhập địa điểm “chợ Bến Thành” trên trang http://google.com/maps, sau đó nháy chuột phải vào địa điểm đó trên bản đồ ta được thông tin về kinh độ, vĩ độ như hình 13. Hãy viết tọa độ địa lí của chợ bến thành thuộc thành phố Hồ Chí Minh. Hãy viết tọa độ địa lí của chợ Bến Thành thuộc thành phố Hồ chí Minh.
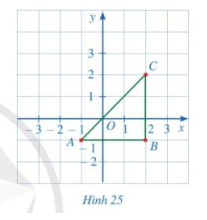
Cho tam giác ABC như hình 25
a) Xác định tọa độ các điểm A, B, C
b) Tam giác ABC có là tam giác vuông cân hay không?
c) Gọi D là điểm để tứ giác ABCD là hình vuông. Xác định tọa độ điểm D.
Trong mặt phẳng tọa độ \(Oxy\), xác định tọa độ điểm \(A\) trong mỗi trường hợp sau:
a) Hoành độ bằng -2 và tung độ bằng 2;
b) Hoành độ bằng 3 và tung độ bằng 4;
c) Tung độ bằng -6 và nằm trên trục tung;
d) Hoành độ bằng \(\frac{1}{2}\) và nằm trên trục hoành.
Trong mặt phẳng tọa độ \(Oxy\), nêu cách xác định mỗi điểm sau:
a) \(M\left( {0;2} \right)\)
b) \(N\left( { - 4;0} \right)\)
c) \(P\left( { - 3; - 3} \right)\)
d) \(Q\left( {5;2} \right)\)
Trong mặt phẳng tọa độ \(Oxy\), cho các điểm \(A\left( { - 4;3} \right),B\left( { - \frac{1}{4}; - \frac{1}{6}} \right),C\left( {2; - \frac{1}{3}} \right)\)
Ba điểm trên nằm ở góc phần tư nào của mặt phẳng tọa độ?
Nhiệt độ \(y\left( {^0C} \right)\) ở một địa điểm thuộc vùng có đới khí hậu hàn đới là một hàm số theo thời điểm \(x\) (h) trong một ngày. Hàm số này được biểu thị dưới dạng Bảng 1.
Trong mặt phẳng tọa độ \(Oxy\), biểu diễn các điểm có tọa độ là các cặp số \(\left( {x;y} \right)\) tương ứng ở Bảng 1.









Danh sách bình luận