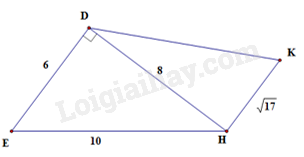
Tìm câu trả lời sai. Cho hình vẽ biết DE // HK. Khi đó:
-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
Ta có DE // HK nên: \(\widehat {E{{D}}H} = \widehat {DHK} = {90^o}\) (so le trong)
Áp dụng định lí Pythagore trong tam giác vuông DHK ta được:
\(D{K^2} = D{H^2} + H{K^2}\)
\(D{K^2} = {8^2} + {\left( {\sqrt {17} } \right)^2}\)
\(D{K^2} = 64 + 17 = 81 = {9^2}\\DK = 9\)
Đáp án : C

Các bài tập cùng chuyên đề
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
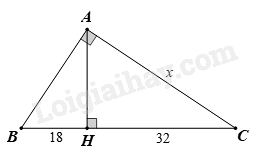
Tính x trong hình sau:
-
A.
36
-
B.
40
-
C.
42
-
D.
30
Cho một tam giác vuông có hai cạnh góc vuông là \(a\), \(b\) và cạnh huyền là \(c\).
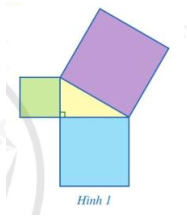
- Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn có cùng có cạnh bằng \(a + b\).
- Đặt bốn tam giác vuông lên hình vuông thứ nhất trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là \(a\) và \(b\). Tính diện tích phần bìa đó là \(a\) và \(b\).
- Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là \(c\). Tính diện tích phần bìa đó theo \(c\).
- Rút ra kết luận về quan hệ giữa \({a^2} + {b^2}\) và \({c^2}\).

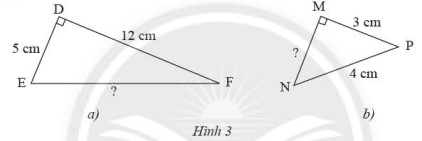
Tính độ dài cạnh \(EF\), \(MN\) của các tam giác vuông trong hình 3.
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là \(72\)cm và \(120\)cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch \( \approx \)\(2,54\)cm).

a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài \(6\)cm và \(8\)cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể).
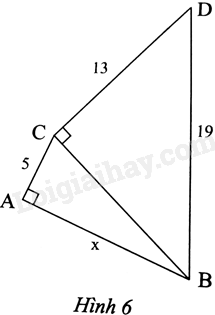
b) Một khung gỗ \(ABCD\) (Hình 6) được tạo thành từ \(5\) thanh nẹp có độ dài như sau: \(AB = CD = 36\)cm; \(BC = AD = 48\)cm; \(AC = 60\)cm. Chứng minh rằng \(\widehat {ABC}\) và \(\widehat {ADC}\) là các góc vuông.

Cho tam giác \(ABC\) vuông tại \(A\).
a) Tính độ dài cạnh \(BC\) nếu biết \(AB = 7\)cm, \(AC = 24\)cm.
b) Tính độ dài cạnh \(AB\) biết \(AC = 2\)cm, \(BC = \sqrt {13} \)cm.
c) Tính độ dài cạnh \(AC\) nếu biết \(BC = 25\)cm, \(AB = 15\)cm.
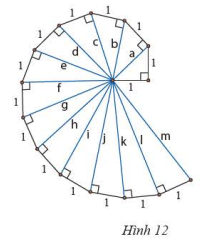
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
Quan sát Hình 1, bạn Đan khẳng định: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?
Thực hiện các hoạt động sau:
a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2)
b) Vẽ hình vuông ABCD có cạnh là b + c như Hình 3. Đặt hình 4 tam giác vuông đã cắt ở câu a lên hình vuông ABCD vừa vẽ, phần chưa bi che đi là hình vuông MNPQ với đọ dài cạnh a (Hình 4)
c) Gọi S1 là diện tích của hình vuông ABCD. Gọi S2 là tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ. So sánh S1 và S2.
d) Dựa vào kết quả ở câu c, dự đoán mỗi liên hệ giữa a2 và b2 + c2.
Tính độ dài đường chéo của hình vuông có độ dài cạnh là a.
Cho tam giác ABC vuông tại A. Tìm độ dài cạnh còn lại trong mỗi trường hợp sau:
a) AB = 8 cm, BC = 17 cm.
b) AB = 20 cm, AC = 21 cm.
c) AB = AC = 6 cm.
Cho tam giác vuông cân có độ dài cạnh góc vuông bằng 1 dm. Tính độ dài cạnh huyền của tam giác đó.
Cho một tam giác đều cạnh a
a) Tính độ dài đường cao của tam giác đó theo a.
b) Tính diện tích của tam giác đó theo a.
Hoàn thành bảng dưới đây bằng cách với mỗi trường hợp, vẽ một tam giác vuông có các cạnh góc vuông bằng \(a\left( {cm} \right)\),\(b\left( {cm} \right)\) và đo độ dài cạnh huyền \(c\left( {cm} \right)\) tương ứng.
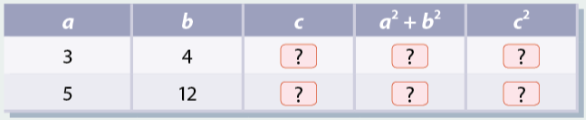
Có nhận xét gì về quan hệ giữa \({c^2}\) và \({a^2} + {b^2}\) trong mỗi trường hợp?

Dùng giấy màu, cắt tám tam giác vuông bằng nhau. Với mỗi tam giác vuông này, gọi độ dài các cạn
h góc vuông là \(a,b\) và độ dài cạnh huyền là \(c\). Dùng giấy bìa trắng, cắt hai hình vuông có cạnh bằng \(a + b\).
1. Đặt bốn tam giác vuông lên tấm bìa hình vuông thứ nhất như hình 3.2. Tính diện tích \({S_1}\) của phần bìa màu trắng không bị che lấp.
2. Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 3.2b. Tính diện tích \({S_2},{S_3}\) của phần bìa màu trắng không bị che lấp.
3. So sánh \({S_1}\) và \({S_2} + {S_3}\), từ đó nhận xét mối quan hệ giữa \({c^2}\) và \({a^2} + {b^2}.\)
Tìm độ dài thích hợp cho ô \(?\).
a) \(\Delta {\rm{DEF}}\) vuông tại \(E\) có \({?^2} + {?^2} = {?^2}\)( định lí Pythagore)
b) \(\Delta MNP\) vuông tại \(P\)có \({?^2} + {?^2} = {?^2}\) ( định lí Pythagore)
c) \(\Delta ABC\) vuông tại \(?\) có \(A{B^2} = A{C^2} + {?^2}\)( định lí Pythagore)
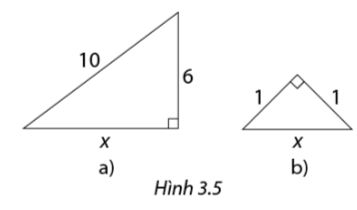
Tìm độ dài \(x\) trong các tam giác vuông ở hình 3.5
Các nhà sản xuất thường dựa vào độ dài đường chéo của màn hình điện thoại (tính theo đơn vị inch) để xác định kích thước màn hình chiếc điện thoại đó. Màn hình một chiếc điện thoại có chiều rộng \(6,9\,cm,\) chiều dài \(15\,cm\) thì có kích thước màn hình là bao nhiêu inch (làm tròn kết quả đến hàng phần mười)? Biết 1 inch\( \approx 3,54\,cm.\)
Hình 3.8 mô phỏng thiết kế của đoạn lên dốc dành cho người ngồi xe lăn trong một công trình xây dựng. Theo quy chuẩn quốc gia về xây dựng công trình đảm bảo người khuyết tật tiếp cận sử dụng (QCVN 10:2014/BXD), độ dốc không được lớn hơn \(\frac{1}{{12}}\), nghĩa là \(\frac{h}{d} \le \frac{1}{{12}}\). Thiết kế này có đáp ứng đúng quy chuẩn trên không?

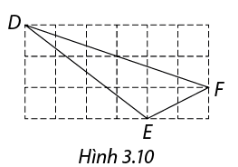
Tam giác DEF được vẽ trên giấy kẻ ô vuông (độ dài cạnh của ô vuông bằng 1) như trong hình 3.10. Tính độ dài cạnh của tam giác DEF.
Tính độ dài đường cao của một tam giác đều có độ dài cạnh bằng \(4cm.\)
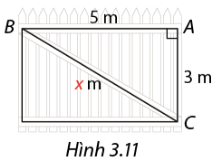
Tính độ dài \(x\,\left( m \right)\) của thanh BC dùng để gia cố hàng rào gỗ trong hình 3.11 (làm tròn kết quả đến hàng phần trăm).
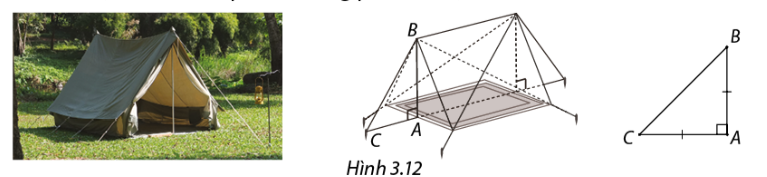
Hình 3.12 là bản vẽ mô tả một lều hình chữ A khi cắm trại, BC là dây lèo, AB là cột chính cao \(1,6m\) và AC là khoảng cách từ chân cột đến vị trí cọc C. Tính độ dài dây BC theo mét (không tính phần dây buộc vào cọc), biết tam giác ABC vuông cân tại A và \(AC = 1,6m\)( làm tròn kết quả đến hàng phần mười).
Tính độ dài các cạnh và đường chéo của tứ giác \(ABCD\) trong Hình 3.23 (ta quy ước độ dài cạnh mỗi ô vuông nhỏ là 1 cm).

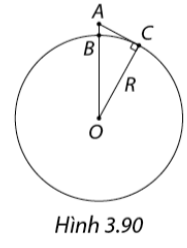
Năm 2019, vệ tinh Tsubame của Nhật Bản được Tổ chức Kỉ lục thế giới Guinness ghi nhận là vệ tinh quan sát Trái Đất ở quỹ đạo thấp nhất. Trong Hình 3.90, vệ tinh Rsubame quan sát mặt đất ở vị trí \(A\) và có độ cao cách bề mặt Trái Đất là \(AB\). Tầm quan sát tối đa của vệ tinh Tsubame là đoạn thẳng \(AC\) có độ dài bằng 1470 km (từ vị trí \(A\), vệ tinh có thể quan sát thấy những nơi trên Trái Đất cách \(A\) không quá 1470 km). Cho biết ba điểm \(A,B,O\) thẳng hàng, bán kính Trái Đất là \(R = OB = OC = 6370km\) và \(AC\) vuông góc với \(OC\). Tính độ cao \(AB\) của vệ tinh Tsubame so với mặt đất theo kilomet (làm tròn kết quả đến hàng phần mười).
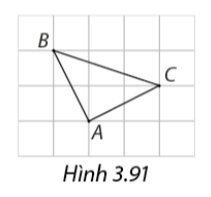
Chứng minh tam giác \(ABC\) vẽ trên giấy kẻ ô vuông (Hình 3.91) là tam giác vuông cân.
Cho tam giác MNP vuông tại M.
a) Tính độ dài cạnh NP biết \(MN = 7,MP = 24\).
b) Tính độ dài cạnh MP biết \(NP = 29,MN = 20\).
c) Tính độ dài cạnh MN biết \(NP = 61,MP = 11\).
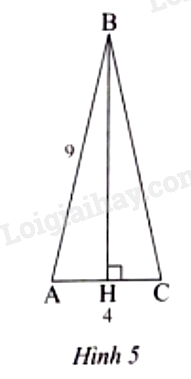
Tính chiều cao BH của tam giác ABC cân tại B (Hình 5), biết \(AB = 9cm\) và \(AC = 4cm\).
Tính độ dài x trong Hình 6