Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo

Hoạt động 4

Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).

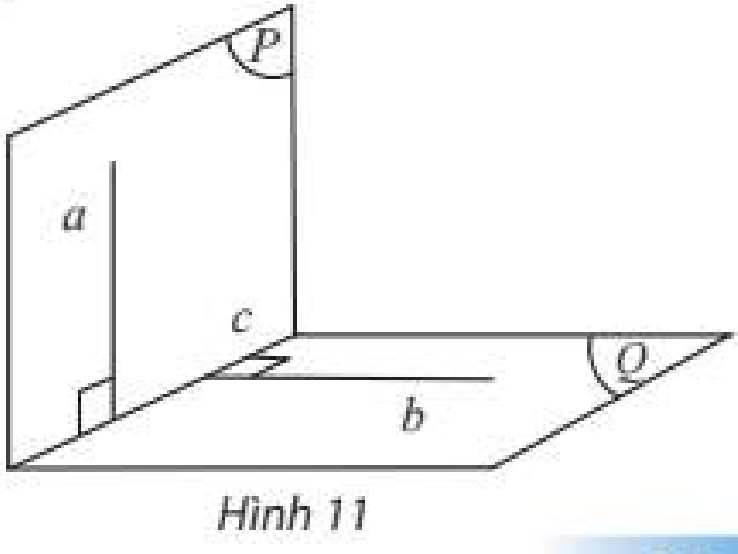
Hỏi:

a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?

b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?

Phương pháp giải:

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Lời giải chi tiết:

a) Ta có:

\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)

b) Ta có:

\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)

Hoạt động 5

Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:

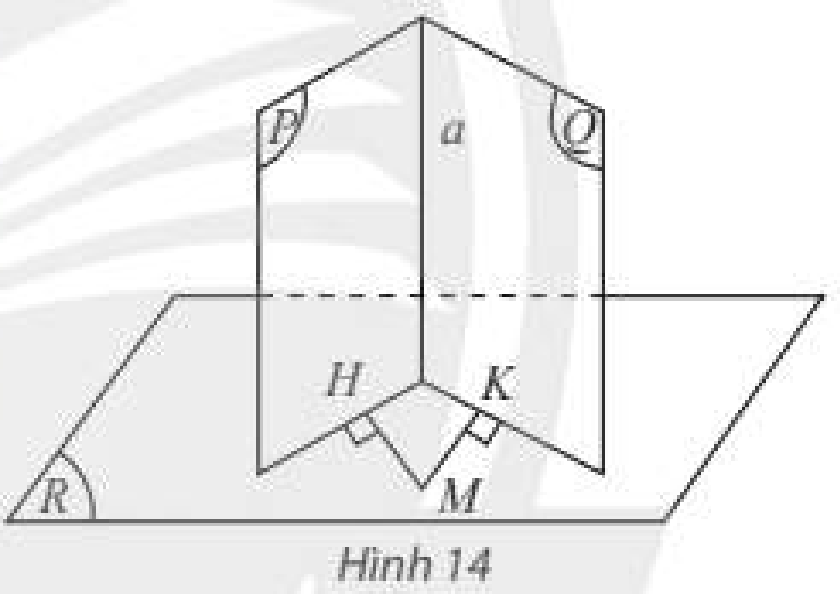
a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?

b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?

Phương pháp giải:

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Lời giải chi tiết:

a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)

b) Ta có:

\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)

Thực hành 2

Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:

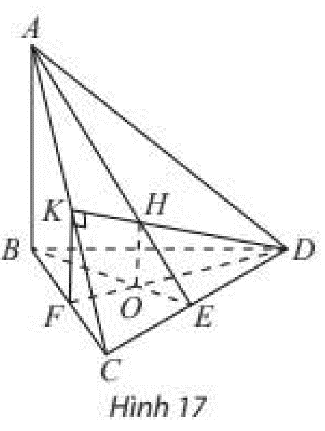
a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);

b) \(OH \bot \left( {ADC} \right)\).

Phương pháp giải:

‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng:

+ Cách 1: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

+ Cách 2: sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Lời giải chi tiết:

a) Ta có:

\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)

Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)

Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)

\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)

Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)

Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)

b) Ta có:

\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)

Vận dụng 2

Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn. 

Phương pháp giải:

Sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Lời giải chi tiết:

Ta mở quyển sách ra và đặt quyển sách lên mặt bàn sao cho hai mép dưới của bìa sách nằm trên mặt bàn.