Đề ôn hè Toán 7 lên 8 - Đề 9

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Trong các số sau, số nào là số hữu tỉ dương?

A. \(\frac{{2021}}{{ - 2022}}\).

B. \(\frac{{ - 2022}}{{2023}}.\)

C. \( - \frac{{2023}}{{2024}}\).

D. \(\frac{{ - 2024}}{{ - 2025}}.\)

Câu 2: Trong các số dưới đây, số nào không có căn bậc hai số học?

A. \(\frac{{64}}{9}\).

B. \( - 1\).

C. \(0\).

D. \(\left| { - 16} \right|\).

Câu 3: Số đối của số \(\left| { - 3} \right|\) là

A. \(\frac{{ - 1}}{3}\).

B. \(\frac{1}{3}\).

C. \( - 3\).

D. \(3\).

Câu 4: Biết \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ là 30. Khi \(x = 15\) thì giá trị của \(y\) là

A. 450.

B. 2.

C. \(\frac{1}{2}\).

D. \(5\).

Câu 5: Cho hình vẽ, biết \(\widehat {{A_2}} = \widehat {{B_2}} = {50^{\rm{o}}}\). Khẳng định nào sau đây là sai?

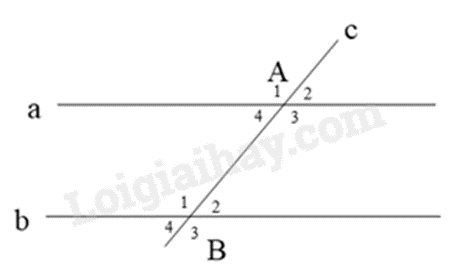
A. \(\widehat {{A_1}} = \widehat {{A_3}}.\)

B. \(\widehat {{A_1}} = \widehat {{B_3}} = 130^\circ \).

C. \(\widehat {{B_4}} = \widehat {{A_3}} = 50^\circ \).

D. \(\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \).

Câu 6: Một máy lọc nước có vỏ dạng hình hộp chữ nhật được làm bằng kính cường lực với chiều cao \(95cm,\) chiều dài \(44\,cm\) và chiều rộng \(35\,cm.\) Diện tích kính cường lực dùng để làm vỏ (không tính phần mép vỏ) là

A. \({\rm{146300 }}c{m^2}.\)

B. \({\rm{15010 }}c{m^2}.\)

C. \(18090{\rm{ }}c{m^2}.\)

D. \(16550{\rm{ }}c{m^2}.\)

Câu 7: Trong các dãy dữ liệu sau, dãy dữ liệu nào không thể sắp thứ tự?

A. Tên một số quốc gia: Việt Nam, Hàn Quốc, Thái Lan, Nhật Bản, Lào.

B. Đánh giá của các bạn học sinh về chất lượng bài giảng: Tốt, Khá, Xuất sắc, Trung bình.

C. Năm sinh của các thành viên trong gia đình nhà bạn Vân: \(1987;1985;2012;2017.\)

D. Cân nặng (đơn vị kilôgam) của năm bạn trong lớp: \(45;46;48;52;42.\)

Câu 8: Một túi đựng sáu tấm thẻ ghi các số \(2;{\rm{ }}3;{\rm{ }}8;{\rm{ }}14;{\rm{ }}22;{\rm{ }}25.\) Rút ngẫu nhiên một tấm thẻ trong túi. Xác suất để rút được thẻ ghi số \(2\) là

A. \(\frac{1}{2}.\)

B. \(\frac{1}{6}.\)

C. \(\frac{2}{3}.\)

D. \(\frac{1}{3}.\)

Câu 9: Đa thức \(A(x) =  - 2{x^3} + 5x - 10 + 2{x^3}\) có nghiệm là

A. \(x =  - 2.\)

B. \(x = \frac{1}{2}.\)

C. \(x = 2.\)

D. \(x = 0.\)

Câu 10: Một tam giác cân có góc ở đỉnh bằng \(52^\circ \) thì số đo góc ở đáy bằng  \(\)

A. \(60^\circ .\)

B. \(64^\circ .\)

C. \(48^\circ .\)

D. \(52^\circ .\)

Câu 11: Cho tam giác \(ABC\) có \(\widehat B > \widehat C\). Khi đó ta có

A. \(AC < AB.\)

B. \(AC > AB.\)

C. \(BC < AC < AB.\)

D. \(BC < AB.\)

Câu 12: Cho hình vẽ:

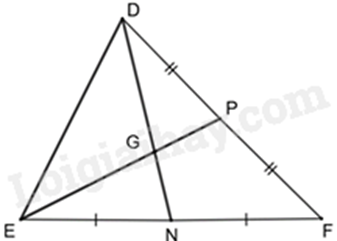
Biết \(DN = 9{\rm{ }}cm\). Độ dài đoạn thẳng \(DG\) bằng

A. \({\rm{3 }}cm.\)

B. \(6{\rm{ }}cm.\)

C. \({\rm{9 }}cm.\)

D. \({\rm{4,5 }}cm.\)

Phần tự luận (7 điểm)

Bài 1. (2,5 điểm)

1. Thực hiện phép tính: \(\frac{3}{5} + \frac{2}{5} \cdot \left( { - 2,5} \right) + 1\frac{2}{5}.\)

2. Cho hai đa thức \(A\left( x \right) = 4{x^2} + 5x - 1\) và \(B\left( x \right) =  - 2x + 3{x^2} - 9\).

a) Tìm đa thức \(C\left( x \right)\) sao cho \(C\left( x \right) = A\left( x \right) + B\left( x \right)\).

b) Xác định bậc, hệ số cao nhất của đa thức \(C(x)\).

3. Tìm \(x\), biết: \(x\left( {x + 2} \right) - {x^2} =  - 16\).

Bài 2. (1 điểm) Do ảnh hưởng của hoàn lưu bão số 3 (bão Yagi), nhiều địa phương tại khu vực miền núi phía Bắc nước ta đã có mưa lớn dẫn đến lũ quét, sạt lở ở nhiều nơi, gây thiệt hại nặng nề về người và của. Hưởng ứng tinh thần tương thân tương ái, lá lành đùm lá rách, ba lớp 7A, 7B và 7C của trường THCS X đã thực hiện quyên góp được 218 quyển vở để giúp đỡ các bạn học sinh vùng cao bị ảnh hưởng bởi bão. Biết lớp 7A có 35 học sinh, lớp 7B có 36 học sinh, lớp 7C có 38 học sinh và số vở ba lớp quyên góp được tỉ lệ với số học sinh của mỗi lớp. Hỏi mỗi lớp quyên góp được bao nhiêu quyển vở?

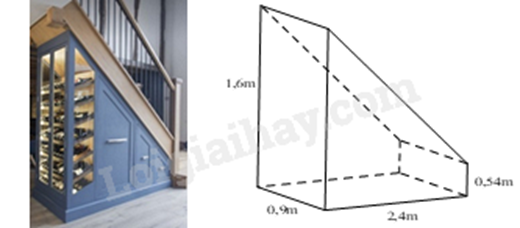
Bài 3. (1 điểm) Để tiết kiệm không gian, gia đình bạn T đã đặt ở phía dưới gầm cầu thang một chiếc tủ có dạng hình lăng trụ đứng có chiều cao bằng \(0,9\,m\) và đáy (mặt bên của tủ) là một hình thang vuông có độ dài đáy lớn bằng \(1,6\,m\), đáy nhỏ bằng \(0,54\,m\), chiều cao bằng \(2,4\,m\) (tham khảo hình vẽ). Hỏi chiếc tủ đó có thể tích xấp xỉ bằng bao nhiêu mét khối? (làm tròn kết quả đến chữ số thập phân thứ ba.)  

Bài 4. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(A\), \(M\) là trung điểm của \(BC\). Từ điểm \(M\) vẽ đường thẳng \(ME\) vuông góc với \(AB\)\(\left( {E \in AB} \right)\) và vẽ đường thẳng \(MF\) vuông góc với \(AC\)\(\left( {F \in AC} \right)\).

a) Chứng minh \(\Delta BME{\rm{ }} = \Delta CMF\).

b) Chứng minh \(AE{\rm{ }} = {\rm{ }}AF\).

Bài 5. (1 điểm) Nhóm 1 của lớp 7A gồm bốn bạn học sinh nam: Thanh, Tú, Tùng, Tiến. Chọn ngẫu nhiên 1 bạn từ danh sách các bạn nhóm 1. Biết mỗi bạn đều có cùng khả năng được chọn. Cho các biến cố sau:

A: “Bạn được chọn tên Thanh”.

B: “Bạn đượn chọn có tên bắt đầu bằng chữ cái T”.

C: “Bạn được chọn là bạn nữ”.

a) Trong các biến cố trên, hãy chỉ ra biến cố nào là chắc chắn, không thể, ngẫu nhiên.

b) Tính xác suất của biến cố C.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Trong các số sau, số nào là số hữu tỉ dương?

A. \(\frac{{2021}}{{ - 2022}}\).

B. \(\frac{{ - 2022}}{{2023}}.\)

C. \( - \frac{{2023}}{{2024}}\).

D. \(\frac{{ - 2024}}{{ - 2025}}.\)

Phương pháp

Số hữu tỉ dương là số lớn hơn 0.

Lời giải

Số \(\frac{{ - 2024}}{{ - 2025}} = \frac{{2024}}{{2025}} > 0\) nên là số hữu tỉ dương.

Đáp án: D.

Câu 2: Trong các số dưới đây, số nào không có căn bậc hai số học?

A. \(\frac{{64}}{9}\).

B. \( - 1\).

C. \(0\).

D. \(\left| { - 16} \right|\).

Phương pháp

Số có căn bậc hai số học là số không âm.

Lời giải

Vì -1 < 0 nên -1 không có căn bậc hai số học.

Đáp án: B.

Câu 3: Số đối của số \(\left| { - 3} \right|\) là

A. \(\frac{{ - 1}}{3}\).

B. \(\frac{1}{3}\).

C. \( - 3\).

D. \(3\).

Phương pháp

\(\left| a \right| = a\) nếu \(a \ge 0\);

\(\left| a \right| =  - a\) nếu \(a < 0\).

Số đối của a là –a.

Lời giải

Ta có: \(\left| { - 3} \right| = 3\).

Số đối của 3 là -3.

Đáp án: C.

Câu 4: Biết \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ là 30. Khi \(x = 15\) thì giá trị của \(y\) là

A. 450.

B. 2.

C. \(\frac{1}{2}\).

D. \(5\).

Phương pháp

Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ \(a = xy\).

Từ đó tính được \(y = \frac{a}{x}\).

Lời giải

Khi \(x = 15\) thì \(y = \frac{{30}}{{15}} = 2\).

Đáp án: B.

Câu 5: Cho hình vẽ, biết \(\widehat {{A_2}} = \widehat {{B_2}} = {50^{\rm{o}}}\). Khẳng định nào sau đây là sai?

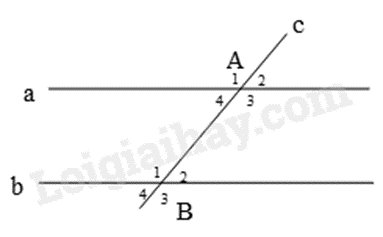
A. \(\widehat {{A_1}} = \widehat {{A_3}}.\)

B. \(\widehat {{A_1}} = \widehat {{B_3}} = 130^\circ \).

C. \(\widehat {{B_4}} = \widehat {{A_3}} = 50^\circ \).

D. \(\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \).

Phương pháp

- Nếu một đường thẳng cắt hai đường thẳng tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.

- Tính chất hai đường thẳng song song: Hai góc so le trong bằng nhau, hai góc so le ngoài bằng nhau, hai góc đồng vị bằng nhau.

- Hai góc đối đỉnh bằng nhau.

- Hai góc kề bù có tổng bằng \(180^\circ \).

Lời giải

Vì \(\widehat {{A_2}} = \widehat {{B_2}} = {50^{\rm{o}}}\), mà hai góc này ở vị trí đồng vị nên a // b.

Vì \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \), suy ra \(\widehat {{A_1}} = 180^\circ  - \widehat {{A_2}} = 180^\circ  - 50^\circ  = 130^\circ \).

Vì \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}} = \widehat {{A_3}}\), đáp án A đúng.

Vì \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\) là hai góc so le ngoài nên \(\widehat {{A_1}} = \widehat {{B_3}} = 130^\circ \), đáp án B đúng.

Vì \(\widehat {{A_1}} = \widehat {{A_3}} = 130^\circ \) mà \(\widehat {{B_4}} = 50^\circ \left( { = \widehat {{B_2}}} \right)\) (hai góc đối đỉnh) nên \(\widehat {{B_4}} \ne \widehat {{A_3}}\), đáp án C sai.

Vì \(\widehat {{A_4}} = \widehat {{B_4}}\) nên \(\widehat {{A_4}} + \widehat {{B_3}} = \widehat {{B_4}} + \widehat {{B_3}} = 180^\circ \) (hai góc kề bù), đáp án D đúng.

Đáp án: D.

Câu 6: Một máy lọc nước có vỏ dạng hình hộp chữ nhật được làm bằng kính cường lực với chiều cao \(95cm,\) chiều dài \(44\,cm\) và chiều rộng \(35\,cm.\) Diện tích kính cường lực dùng để làm vỏ (không tính phần mép vỏ) là

A. \({\rm{146300 }}c{m^2}.\)

B. \({\rm{15010 }}c{m^2}.\)

C. \(18090{\rm{ }}c{m^2}.\)

D. \(16550{\rm{ }}c{m^2}.\)

Phương pháp

Tính diện tích toàn phần của hình hộp chữ nhật = S_xq + S_{2 đáy}.

Lời giải

Diện tích xung quanh của hình hộp chữ nhật là: \({S_{xq}} = C.h = 2\left( {35 + 44} \right).95 = 15010\left( {c{m^2}} \right)\).

Diện tích đáy của hình hộp chữ nhật là: S_đáy = \(35.44 = 1540\left( {c{m^2}} \right)\)

Diện tích kích cường lực dùng để làm vỏ là: \(15010 + 2.1540 = 18090\left( {c{m^2}} \right)\)

Đáp án: C.

Câu 7: Trong các dãy dữ liệu sau, dãy dữ liệu nào không thể sắp thứ tự?

A. Tên một số quốc gia: Việt Nam, Hàn Quốc, Thái Lan, Nhật Bản, Lào.

B. Đánh giá của các bạn học sinh về chất lượng bài giảng: Tốt, Khá, Xuất sắc, Trung bình.

C. Năm sinh của các thành viên trong gia đình nhà bạn Vân: \(1987;1985;2012;2017.\)

D. Cân nặng (đơn vị kilôgam) của năm bạn trong lớp: \(45;46;48;52;42.\)

Phương pháp

Dữ liệu được chia thành:

- Dữ liệu là số (số liệu)

- Dữ liệu không là số

+ Không thể sắp thứ tự

+ Có thể sắp thứ tự

Lời giải

Dữ liệu không thể sắp thứ tự là: Tên một số quốc gia: Việt Nam, Hàn Quốc, Thái Lan, Nhật Bản, Lào.

Đáp án: A.

Câu 8: Một túi đựng sáu tấm thẻ ghi các số \(2;{\rm{ }}3;{\rm{ }}8;{\rm{ }}14;{\rm{ }}22;{\rm{ }}25.\) Rút ngẫu nhiên một tấm thẻ trong túi. Xác suất để rút được thẻ ghi số \(2\) là

A. \(\frac{1}{2}.\)

B. \(\frac{1}{6}.\)

C. \(\frac{2}{3}.\)

D. \(\frac{1}{3}.\)

Phương pháp

Xác định các kết quả có thể là \(k\).

Các kết quả là đồng khả năng nên xác suất là \(\frac{1}{k}\).

Lời giải

Có 6 tấm thẻ.

Khả năng rút được mỗi tấm thẻ là ngẫu nhiên nên xác suất để rút được thẻ ghi số 2 là \(\frac{1}{6}\).

Đáp án: B.

Câu 9: Đa thức \(A(x) =  - 2{x^3} + 5x - 10 + 2{x^3}\) có nghiệm là

A. \(x =  - 2.\)

B. \(x = \frac{1}{2}.\)

C. \(x = 2.\)

D. \(x = 0.\)

Phương pháp

Đa thức \(A\left( x \right)\) có nghiệm khi \(A\left( x \right) = 0\).

Lời giải

Ta có: \(A(x) =  - 2{x^3} + 5x - 10 + 2{x^3} = \left( { - 2{x^3} + 2{x^3}} \right) + 5x - 10 = 5x - 10\).

Đa thức A(x) có nghiệm khi

\(A\left( x \right) = 0\)

\(\begin{array}{l}5x - 10 = 0\\5x = 10\\x = 2\end{array}\)

Vậy \(x = 2\).

Đáp án: C.

Câu 10: Một tam giác cân có góc ở đỉnh bằng \(52^\circ \) thì số đo góc ở đáy bằng  \(\)

A. \(60^\circ .\)

B. \(64^\circ .\)

C. \(48^\circ .\)

D. \(52^\circ .\)

Phương pháp

Sử dụng tính chất tam giác cân có hai góc ở đáy bằng nhau.

Tổng ba góc trong tam giác bằng \(180^\circ \).

Lời giải

Vì tam giác cân nên hai góc ở đáy bằng nhau.

Do đó số đo góc ở đáy bằng: \(\frac{{180^\circ  - 52^\circ }}{2} = 64^\circ \).

Đáp án: B.

Câu 11: Cho tam giác \(ABC\) có \(\widehat B > \widehat C\). Khi đó ta có

A. \(AC < AB.\)

B. \(AC > AB.\)

C. \(BC < AC < AB.\)

D. \(BC < AB.\)

Phương pháp

Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác.

Lời giải

Xét \(\Delta ABC\) có \(\widehat B > \widehat C\) nên \(AC > AB\) (quan hệ giữa góc và cạnh đối diện trong tam giác).

Đáp án: B.

Câu 12: Cho hình vẽ:

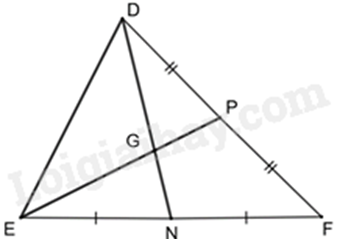
Biết \(DN = 9{\rm{ }}cm\). Độ dài đoạn thẳng \(DG\) bằng

A. \({\rm{3 }}cm.\)

B. \(6{\rm{ }}cm.\)

C. \({\rm{9 }}cm.\)

D. \({\rm{4,5 }}cm.\)

Phương pháp

Sử dụng tính chất của trọng tâm: khoảng cách từ đỉnh đến trọng tâm bằng \(\frac{2}{3}\) độ dài đường trung tuyến tương ứng.

Lời giải

Vì P là trung điểm của DF và N là trung điểm của EF nên EP và DN là hai đường trung tuyến của tam giác DEF.

Mà DN và EP cắt nhau tại G nên G là trọng tâm của tam giác DEF.

Do đó DG = \(\frac{2}{3}\)DN = \(\frac{2}{3}\).9 = 6 (cm)

Đáp án: B.

Phần tự luận.

Bài 1. (2,5 điểm)

1. Thực hiện phép tính: \(\frac{3}{5} + \frac{2}{5} \cdot \left( { - 2,5} \right) + 1\frac{2}{5}.\)

2. Cho hai đa thức \(A\left( x \right) = 4{x^2} + 5x - 1\) và \(B\left( x \right) =  - 2x + 3{x^2} - 9\).

a) Tìm đa thức \(C\left( x \right)\) sao cho \(C\left( x \right) = A\left( x \right) + B\left( x \right)\).

b) Xác định bậc, hệ số cao nhất của đa thức \(C(x)\).

3. Tìm \(x\), biết: \(x\left( {x + 2} \right) - {x^2} =  - 16\).

Phương pháp

1. Đưa về dạng biểu diễn phân số để tính.

2) a) Nhóm các hạng tử có cùng số mũ để tính.

b) Bậc là số mũ cao nhất của \(x\), hệ số cao nhất là hệ số của hạng tử có số mũ cao nhất.

3) Nhân đơn thức với đa thức rồi rút gọn, chuyển vế tìm \(x\).

Lời giải

1.

\(\frac{3}{5} + \frac{2}{5} \cdot \left( { - 2,5} \right) + 1\frac{2}{5}\)\( = \frac{3}{5} + \frac{2}{5} \cdot \frac{{ - 5}}{2} + \frac{7}{5}\)

\( = \left( {\frac{3}{5} + \frac{7}{5}} \right) - 1 = 2 - 1 = 1\)

2.

a) Ta có \(C\left( x \right) = A\left( x \right) + B\left( x \right)\)\( = \left( {4{x^2} + 5x - 1} \right) + \left( { - 2x + 3{x^2} - 9} \right)\)

\( = 4{x^2} + 5x - 1 - 2x + 3{x^2} - 9\)

\( = \left( {4{x^2} + 3{x^2}} \right) + \left( {5x - 2x} \right) - \left( {1 + 9} \right)\)\( = 7{x^2} + 3x - 10\)

b) Bậc: \(2\); Hệ số cao nhất: \(7\)

3.

\(x\left( {x + 2} \right) - {x^2} =  - 16\)

\({x^2} + 2x - {x^2} =  - 16\)

\(2x =  - 16\)

\(x =  - 16:2\)

\(x =  - 8\)

Vậy \(x =  - 8\).

Bài 2. (1 điểm) Do ảnh hưởng của hoàn lưu bão số 3 (bão Yagi), nhiều địa phương tại khu vực miền núi phía Bắc nước ta đã có mưa lớn dẫn đến lũ quét, sạt lở ở nhiều nơi, gây thiệt hại nặng nề về người và của. Hưởng ứng tinh thần tương thân tương ái, lá lành đùm lá rách, ba lớp 7A, 7B và 7C của trường THCS X đã thực hiện quyên góp được 218 quyển vở để giúp đỡ các bạn học sinh vùng cao bị ảnh hưởng bởi bão. Biết lớp 7A có 35 học sinh, lớp 7B có 36 học sinh, lớp 7C có 38 học sinh và số vở ba lớp quyên góp được tỉ lệ với số học sinh của mỗi lớp. Hỏi mỗi lớp quyên góp được bao nhiêu quyển vở?

Phương pháp

Gọi số quyển vở lớp 7A, 7B, 7C đã quyên góp lần lượt là \(x,y,z\) (quyển, \(x,y,z \in \mathbb{N}{\rm{*}}\)).

Theo đầu bài, ta có: \(\frac{x}{{35}} = \frac{y}{{36}} = \frac{z}{{38}}\) và \(x + y + z = 218.\)

Áp dụng tính chất của dãy tỉ số bằng nhau để tìm \(x,y,z\).

Lời giải

Gọi số quyển vở lớp 7A, 7B, 7C đã quyên góp lần lượt là \(x,y,z\) (quyển, \(x,y,z \in \mathbb{N}{\rm{*}}\)).

Theo đầu bài, ta có: \(\frac{x}{{35}} = \frac{y}{{36}} = \frac{z}{{38}}\) và \(x + y + z = 218.\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{{35}} = \frac{y}{{36}} = \frac{z}{{38}} = \frac{{x + y + z}}{{35 + 36 + 38}} = \frac{{218}}{{109}} = 2.\)

Từ đó suy ra: \(x = 70,y = 72,z = 76\) (thỏa mãn điều kiện)

Vậy số vở ba lớp 7A, 7B, 7C đã quyên góp lần lượt là 70 quyển, 72 quyển, 76 quyển

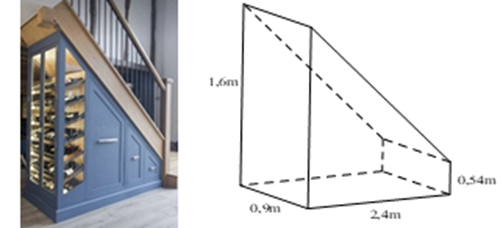
Bài 3. (1 điểm) Để tiết kiệm không gian, gia đình bạn T đã đặt ở phía dưới gầm cầu thang một chiếc tủ có dạng hình lăng trụ đứng có chiều cao bằng \(0,9\,m\) và đáy (mặt bên của tủ) là một hình thang vuông có độ dài đáy lớn bằng \(1,6\,m\), đáy nhỏ bằng \(0,54\,m\), chiều cao bằng \(2,4\,m\) (tham khảo hình vẽ). Hỏi chiếc tủ đó có thể tích xấp xỉ bằng bao nhiêu mét khối? (làm tròn kết quả đến chữ số thập phân thứ ba.)

Phương pháp

Xác định mặt đáy, chiều cao.

Thể tích hình lăng trụ đứng tam giác: V = S_{đáy . h.}

Lời giải

Diện tích đáy là: \(\frac{{\left( {0,54 + 1,6} \right).2,4}}{2} = 2,568\left( {{m^2}} \right)\)

Thể tích chiếc tủ là: \(2,568.0,9 = 2,3112 \approx 2,331\left( {{m^3}} \right)\)

Vậy chiếc tủ đó có thể tích xấp xỉ 2,331\({m^3}\).

Bài 4. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(A\), \(M\) là trung điểm của \(BC\). Từ điểm \(M\) vẽ đường thẳng \(ME\) vuông góc với \(AB\)\(\left( {E \in AB} \right)\) và vẽ đường thẳng \(MF\) vuông góc với \(AC\)\(\left( {F \in AC} \right)\).

a) Chứng minh \(\Delta BME{\rm{ }} = \Delta CMF\).

b) Chứng minh \(AE{\rm{ }} = {\rm{ }}AF\).

Phương pháp

a) Chứng minh \(\widehat B = \widehat C\).

Suy ra \(\Delta BME = \Delta CMF\)(cạnh huyền – góc nhọn)   

b) Chứng minh \(BE = CF\) (2 cạnh tương ứng) và \(AB = AC\) (gt)

nên \(AE = AF\).

Lời giải

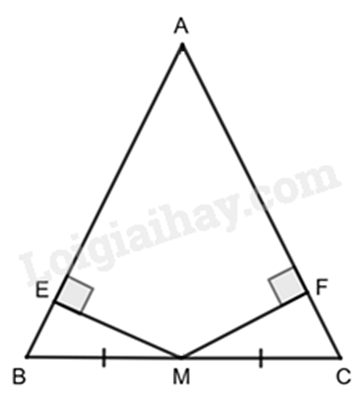
a) Vì \(\Delta ABC\)cân tại \(A\) nên \(\widehat B = \widehat C\).

Xét \(\Delta BME\) và \(\Delta CMF\)có:

\(\widehat {BEM} = \widehat {CFM} = 90^\circ \)(gt)

\(MB{\rm{ }} = {\rm{ }}MC\)(gt) 

\(\widehat B = \widehat C\) (chứng minh trên)    

Suy ra \(\Delta BME = \Delta CMF\)(cạnh huyền – góc nhọn)   

b) Vì \(\Delta BME = \Delta CMF\) (phần a) nên \(BE = CF\) (2 cạnh tương ứng)

Mà \(AB = AC\) (gt)

Suy ra \(AB - BE = AC - CF\)

\(AE = AF\)

Bài 5. (1 điểm) Nhóm 1 của lớp 7A gồm bốn bạn học sinh nam: Thanh, Tú, Tùng, Tiến. Chọn ngẫu nhiên 1 bạn từ danh sách các bạn nhóm 1. Biết mỗi bạn đều có cùng khả năng được chọn. Cho các biến cố sau:

A: “Bạn được chọn tên Thanh”.

B: “Bạn đượn chọn có tên bắt đầu bằng chữ cái T”.

C: “Bạn được chọn là bạn nữ”.

a) Trong các biến cố trên, hãy chỉ ra biến cố nào là chắc chắn, không thể, ngẫu nhiên.

b) Tính xác suất của biến cố C.

Phương pháp

a) - Biến cố chắc chắn là biến cố biết trước được luôn xảy ra.

- Biến cố không thể là biến cố biết trước được không bao giờ xảy ra.

- Biến cố ngẫu nhiên là biến cố không thể biết trước được có xảy ra hay không.

b) Khả năng xảy ra của biến cố chắc chắn là 100%. Vậy biến cố chắc chắn có xác suất bằng 1.
Khả năng xảy ra của biến cố không thể là 0%. Vậy biến cố không thể có xác suất bằng 0.

Lời giải

a) Biến cố A là biến cố ngẫu nhiên.

Biến cố B là biến cố chắc chắn.

Biến cố C là biến cố không thể.

b) Vì C là biến cố không thể nên xác suất bằng 0.