Dạng bài toán thực tế - Ôn hè Toán 7 lên 8

Lý thuyết

* Giải bài toán thực tế bằng cách viết biểu thức

- Bước 1: Đặt biến \(x\) là một đại lượng chưa biết.

- Bước 2: Biểu diễn các đại lượng còn lại theo biến \(x\).

- Bước 3: Viết biểu thức đề bài yêu cầu.

- Bước 4: Xử lý biểu thức.

* Giải bài toán thực tế bằng cách lập đa thức

- Bước 1: Xác định biến \(x\).

- Bước 2: Thể hiện các đại lượng chưa biết theo đại lượng đã biết và theo biến \(x\).

- Bước 3: Xây dựng đa thức biểu thị mối quan hệ giữa các đại lượng.

- Bước 4: Thực hiện các yêu cầu của đề bài.

Bài tập

Bài 1: Viết biểu thức đại số biểu thị tổng quãng đường đi được của một người, biết rằng người đó đi bộ trong \(x\) giờ với vận tốc 4 km/giờ và sau đó đi bằng xe đạp trong \(y\) giờ với vận tốc 18 km/giờ.

A. \(4\left( {x + y} \right)\).

B. \(22\left( {x + y} \right)\).

C. \(4y + 18x\).

D. \(4x + 18y\).

Bài 2: Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá 10000 đồng là:

A. \(10000.x\).

B. \(x + 10000\).

C. \(\frac{{10000}}{x}\).

D. \(\frac{x}{{10000}}\).

Bài 3: Cho mảnh đất có kích thước như sau:

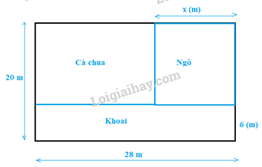
Biết phần đất trồng khoai có dạng hình chữ nhật có kích thước 28 m x 6 m. Biểu diễn diện tích phần đất trồng cà chua theo x

A. 20.x (m²).

B. 392 - 14.x (m²).

C. 560 - 14.x (m²).

D. 14.x (m²).

Bài 4: Một bể đang chứa 480 lít nước, có một vòi chảy vào mỗi phút chảy được \(x\) lít. Cùng lúc đó một vòi khác chảy nước từ bể ra. Mỗi phút lượng nước chảy ra bằng \(\frac{1}{4}\) lượng nước chảy vào. Hãy biểu thị lượng nước trong bể sau khi đồng thời mở cả hai vòi trên sau \(a\) phút.

A. \(480 - \frac{3}{4}ax\) (lít).

B. \(\frac{3}{4}ax\) (lít).

C. \(480 + \frac{3}{4}ax\) (lít).

D. \(480 + ax\) (lít).

Bài 5: Dùng biểu thức toán học để biểu thị các tình huống sau:
a) Một cuốn vở viết giá 5000 đồng. Hỏi mua x cuốn vở viết như thế hết bao nhiêu tiền?
b) Năm nay thầy giáo 40 tuổi. Hỏi x năm nữa thầy giáo bao nhiêu tuổi?
c) Một người chạy thể dục buổi sáng với vận tốc trung bình x (km/h), mỗi sáng người đó chạy nửa giờ.
Hỏi trung bình mỗi sáng người đó chạy thể dục được bao nhiêu km?
d) Một mảnh đất hình chữ nhật có chiều dài là x mét, chiều rộng kém chiều dài 20 mét. Tính chu vi mảnh
đất.

Bài 6: Một hình thang có độ dài đáy lớn là \(x\) mét, đáy bé có độ dài nhỏ hơn đáy lớn 5 mét, chiều cao gấp 2 lần đáy bé.

a) Viết biểu thức tính diện tích hình thang.

b) Nếu \(x = 8\) thì diện tích hình thang là bao nhiêu?

Bài 7: Một cửa hàng bán trà sữa với giá 20 000 đồng/cốc. Nếu mua từ 10 cốc thì được giảm giá 10%, nếu mua trên 30 cốc thì giảm 10% và giảm thêm 50 000 đồng. Gọi số cốc khách mua là x, em hãy xây dựng công thức tính tiền giúp cửa hàng trong các trường hợp:

a) Khách mua dưới 10 cốc.

b) Khách mua từ 10 đến 30 cốc.

c) Khách mua trên 30 cốc.

Bài 8: Một người muốn tính diện tích thửa ruộng hình chữ nhật của nhà mình, nhưng vì không có thước đủ dài nên anh ta dùng một đoạn dây để đo. Anh ta đo thấy rằng chiều rộng thửa ruộng bằng 3,5 lần độ dài đoạn dây, còn chiều dài bằng 10,5 lần độ dài đoạn dây. Gọi đoạn dây có độ dài là x mét, em hãy xây dựng công thức tính diện tích thửa ruộng theo biến x. Nếu độ dài đoạn dây là 5 mét thì diện tích thửa ruộng là bao nhiêu?

Bài 9: Chào mừng ngày nhà giáo Việt Nam 20/11, trường của An tổ chức cho các bạn học sinh các khối thi đấu bóng đá. Các đội thi đấu theo thể thức vòng tròn một lượt. Tổng số trận các bạn đã thi đấu được tính bằng cách, lấy số đội tham gia nhân với số đội trừ đi 1 và tất cả chia cho 2.
a) Hãy viết biểu thức biểu diễn tổng số trận đấu dựa trên số đội bóng tham gia.
b) Tính xem có bao nhiêu trận đấu diễn ra nếu có 5 đội bóng.

Bài 10: Biết rằng nếu độ dài mỗi cạnh của hộp hình lập phương tăng thêm 2 cm thì diện tích phải sơn 6 mặt bên ngoài của hộp đó tăng thêm 216 cm². Tính độ dài cạnh của chiếc hộp hình lập phương đó?

--------Hết--------

Lời giải chi tiết:

Bài 1: Viết biểu thức đại số biểu thị tổng quãng đường đi được của một người, biết rằng người đó đi bộ trong \(x\) giờ với vận tốc 4 km/giờ và sau đó đi bằng xe đạp trong \(y\) giờ với vận tốc 18 km/giờ.

A. \(4\left( {x + y} \right)\).

B. \(22\left( {x + y} \right)\).

C. \(4y + 18x\).

D. \(4x + 18y\).

Phương pháp

Áp dụng công thức: quãng đường = vận tốc . thời gian

Quãng đường đi được = quãng đường đi bộ + quãng đường đi xe đạp

Lời giải

Quãng đường mà người đó đi bộ là: \(4.x = 4x\)

Quãng đường mà người đó đi bằng xe máy là: \(18.y = 18y\)

Tổng quãng đường đi được của người đó là: \(4x + 18y\)

Đáp án:

Bài 2: Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá 10000 đồng là:

A. \(10000.x\).

B. \(x + 10000\).

C. \(\frac{{10000}}{x}\).

D. \(\frac{x}{{10000}}\).

Phương pháp

Dựa vào các kiến thức về biểu thức đại số.

Lời giải

Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá 10000 đồng là:

\(10000.x\)

Đáp án: A

Bài 3: Cho mảnh đất có kích thước như sau:

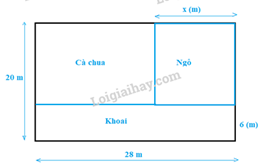
Biết phần đất trồng khoai có dạng hình chữ nhật có kích thước 28 m x 6 m. Biểu diễn diện tích phần đất trồng cà chua theo x

A. 20.x (m²).

B. 392 - 14.x (m²).

C. 560 - 14.x (m²).

D. 14.x (m²).

Phương pháp

Diện tích trồng cà chua = Diện tích vườn – diện tích trồng khoai – diện tích trồng ngô

Diện tích hình chữ nhật = chiều dài . chiều rộng

Lời giải

Tổng diện tích ngô và cà chua bằng diện tích của hình chữ nhật có kích thước 28 m x 14 m nên bằng:

28 . 14 = 392 (m²)

Diện tích trồng ngô là: 14 . x (m²)

Diện tích trồng cà chua là:

392 - 14.x (m²)

Đáp án: B

Bài 4: Một bể đang chứa 480 lít nước, có một vòi chảy vào mỗi phút chảy được \(x\) lít. Cùng lúc đó một vòi khác chảy nước từ bể ra. Mỗi phút lượng nước chảy ra bằng \(\frac{1}{4}\) lượng nước chảy vào. Hãy biểu thị lượng nước trong bể sau khi đồng thời mở cả hai vòi trên sau \(a\) phút.

A. \(480 - \frac{3}{4}ax\) (lít).

B. \(\frac{3}{4}ax\) (lít).

C. \(480 + \frac{3}{4}ax\) (lít).

D. \(480 + ax\) (lít).

Phương pháp

Căn cứ vào nội dung bài toán, viết biểu thức đại số theo yêu cầu đề bài:

+ Tính lượng nước chảy vào trong \(a\) phút

+ Tính lượng nước chảy ra trong \(a\) phút

+ Lượng nước có trong bể sau \(a\) phút = Lượng nước có sẵn + lượng nước chảy vào – lượng nước chảy ra.

Lời giải

Lượng nước chảy vào bể trong \(a\) phút là \(a.x\) (lít).

Lượng nước chảy ra trong \(a\) phút là \(\frac{1}{4}ax\) (lít)

Vì ban đầu bể đang chứa 480 lít nên lượng nước có trong bể sau \(a\) phút là

\(480 + ax - \frac{1}{4}ax = 480 + \frac{3}{4}ax\) (lít)

Đáp án: C

Bài 5: Dùng biểu thức toán học để biểu thị các tình huống sau:
a) Một cuốn vở viết giá 5000 đồng. Hỏi mua x cuốn vở viết như thế hết bao nhiêu tiền?
b) Năm nay thầy giáo 40 tuổi. Hỏi x năm nữa thầy giáo bao nhiêu tuổi?
c) Một người chạy thể dục buổi sáng với vận tốc trung bình x (km/h), mỗi sáng người đó chạy nửa giờ.
Hỏi trung bình mỗi sáng người đó chạy thể dục được bao nhiêu km?
d) Một mảnh đất hình chữ nhật có chiều dài là x mét, chiều rộng kém chiều dài 20 mét. Tính chu vi mảnh
đất.

Phương pháp

Viết biểu thức biểu thị một liên hệ phù hợp.

Lời giải

a) Số tiền mua \(x\) cuốn vở giá 5000 đồng là \(5000x\) (đồng)

b) Tuổi của thầy giáo sau \(x\) năm nữa là: \(40 + x\) (tuổi)

c) Đổi nửa giờ = \(\frac{1}{2}\) giờ.

Trung bình mỗi sáng người đó chạy được \(\frac{1}{2}x\) (km)

d) Chiều rộng mảnh đất là: \(x - 20\) (mét)

Chu vi mảnh đất là: \(\left( {x + x - 20} \right).2 = \left( {2x - 20} \right).2 = 4x - 40\) (mét)

Bài 6: Một hình thang có độ dài đáy lớn là \(x\) mét, đáy bé có độ dài nhỏ hơn đáy lớn 5 mét, chiều cao gấp 2 lần đáy bé.

a) Viết biểu thức tính diện tích hình thang.

b) Nếu \(x = 8\) thì diện tích hình thang là bao nhiêu?

Phương pháp

a) Công thức tính diện tích hình thang bằng: (tổng hai đáy).(chiều cao) : 2.

b) Thay \(x = 8\) vào biểu thức để tính giá trị.

Lời giải

a) Độ dài đáy bé là: \(x - 5\) mét, chiều cao là: 2.(x – 5) mét.

Diện tích hình thang là: \(S = \frac{{\left( {x + x - 5} \right).2\left( {x - 5} \right)}}{2} = \left( {2x - 5} \right)\left( {x - 5} \right)\) \(\left( {{m^2}} \right)\)

b) Khi \(x = 8\) thì diện tích hình thang là: \(S = \left( {2.8 - 5} \right)\left( {8 - 5} \right) = 11.3 = 33\left( {{m^2}} \right)\).

Bài 7: Một cửa hàng bán trà sữa với giá 20 000 đồng/cốc. Nếu mua từ 10 cốc thì được giảm giá 10%, nếu mua trên 30 cốc thì giảm 10% và giảm thêm 50 000 đồng. Gọi số cốc khách mua là x, em hãy xây dựng công thức tính tiền giúp cửa hàng trong các trường hợp:

a) Khách mua dưới 10 cốc.

b) Khách mua từ 10 đến 30 cốc.

c) Khách mua trên 30 cốc.

Phương pháp

Xác định giá tiền các cốc trà sữa trong các trường hợp.

Lời giải

a) Nếu khách mua dưới 10 cốc thì giá mỗi cốc là 20 000 đồng nên số tiền là: \({T_1} = 20\,000x\) (đồng)

b) Nếu khách mua từ 10 đến 30 cốc thì được giảm giá 10% nên số tiền phải trả là: \(20\,000x.\left( {100\%  - 10\% } \right) = 18000x\) (đồng)

c) Nếu khách mua trên 30 cốc thì giảm 10% và giảm thêm 50 000 đồng nên số tiền phải trả là: \(18\,000x - 50\,000\) (đồng)

Bài 8: Một người muốn tính diện tích thửa ruộng hình chữ nhật của nhà mình, nhưng vì không có thước đủ dài nên anh ta dùng một đoạn dây để đo. Anh ta đo thấy rằng chiều rộng thửa ruộng bằng 3,5 lần độ dài đoạn dây, còn chiều dài bằng 10,5 lần độ dài đoạn dây. Gọi đoạn dây có độ dài là x mét, em hãy xây dựng công thức tính diện tích thửa ruộng theo biến x. Nếu độ dài đoạn dây là 5 mét thì diện tích thửa ruộng là bao nhiêu?

Phương pháp

Biểu diễn chiều rộng, chiều dài của thửa ruộng theo \(x\).

Biểu diễn diện tích thửa ruộng theo \(x\).

Thay \(x = 5\) để tính diện tích.

Lời giải

Chiều rộng thửa ruộng là 3,5x mét, chiều dài thửa ruộng là 10,5x mét
Diện tích thửa ruộng là: \(3,5x.10,5x = 36,75{x^2}\left( {{m^2}} \right)\)

Nếu đoạn dây dài 5m thì diện tích là \(36,{75.5^2} = 918,75\left( {{m^2}} \right)\).

Vậy nếu độ dài đoạn dây là 5 mét thì diện tích thửa ruộng là \(918,75{m^2}\).

Bài 9: Chào mừng ngày nhà giáo Việt Nam 20/11, trường của An tổ chức cho các bạn học sinh các khối thi đấu bóng đá. Các đội thi đấu theo thể thức vòng tròn một lượt. Tổng số trận các bạn đã thi đấu được tính bằng cách, lấy số đội tham gia nhân với số đội trừ đi 1 và tất cả chia cho 2.
a) Hãy viết biểu thức biểu diễn tổng số trận đấu dựa trên số đội bóng tham gia.
b) Tính xem có bao nhiêu trận đấu diễn ra nếu có 5 đội bóng.

Phương pháp

Gọi \(x\) là số đội bóng tham gia thi đấu.

a) Xác định biểu thức biểu diễn trân đấu theo đề bài.

b) Thay \(x = 5\) để tìm T.

Lời giải

Gọi \(x\) là số đội bóng tham gia thi đấu.

a) Vì tổng số trận các bạn đã thi đấu được tính bằng cách, lấy số đội tham gia nhân với số đội trừ đi 1 và tất cả chia cho 2 nên ta có biểu thức: \(T = \frac{{x\left( {x - 1} \right)}}{2}\) (trận).

b) Nếu có 5 đội bóng thì số trận đấu diễn ra là: \(T = \frac{{5\left( {5 - 1} \right)}}{2} = 10\).

Bài 10: Biết rằng nếu độ dài mỗi cạnh của hộp hình lập phương tăng thêm 2 cm thì diện tích phải sơn 6 mặt bên ngoài của hộp đó tăng thêm 216 cm². Tính độ dài cạnh của chiếc hộp hình lập phương đó?

Phương pháp

Tính diện tích phải sơn của một mặt tăng thêm.

Gọi độ dài của chiếc hộp ban đầu là x.

Sử dụng công thức tính diện tích hình vuông để viết biểu thức tìm x.

Lời giải

Diện tích phải sơn một mặt của hình hộp tăng thêm là:

216: 6 = 36 (cm²)

Gọi độ dài cạnh của hình lập phương là x (cm) (x > 0), cạnh của hình lập phương mới là: x + 2 (cm)

Diện tích một mặt của hộp ban đầu là: x² (cm²)

Diện tích một mặt của hộp sau khi tăng mỗi cạnh 2 cm là: (x + 2)² (cm²)

Vì diện tích phải sơn một mặt của hộp tăng thêm 36 cm² nên ta có:

\({\left( {x + 2} \right)^2} - {x^2} = 36\)

\({\rm{\;}}\left( {x + 2} \right).\left( {x + 2} \right) - {x^2} = 36\)

\({\rm{\;}}{x^2} + 2x + 2x + 4 - {x^2} = 36\)

\({\rm{\;}}4x + 4 = 36\)

\(4x = 32\)

\({\rm{\;}}x = 8\)

Vậy độ dài cạnh của chiếc hộp lập phương bằng 8 cm.