Dạng bài tìm m để đa thức chia hết cho đa thức - Ôn hè Toán 7 lên 8
Tải vềDạng 6. Tìm m để đa thức chia hết cho đa thức
Lý thuyết
* Quy tắc chia đa thức một biến đã sắp xếp
Để chia một đa thức cho một đa thức khác không (đa thức đã thu gọn, sắp xếp đa thức một biến theo luỹ thừa giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia:
Bước 1.
- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
- Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2.
Tiếp tục quá trình trên cho đến khi nhận được đa thức 0 hoặc đa thức có bậc nhỏ hơn đa thức chia.
Chú ý: Người ta chứng minh được rằng: đối với hai đa thức của cùng một biến tuỳ ý A và B, \(B \ne 0\) tồn tại duy nhất Q và R sao cho \(A = B.Q + R\), với \(R = 0\) hoặc bậc của \(R\) nhỏ hơn bậc của B.
+ Với \(R = 0\), ta nói A chia hết cho B.
+ Với \(R \ne 0\), ta nói A không chia hết cho B (phép chia có dư).
* Tìm m để đa thức A chia hết cho đa thức B
- Thực hiện phép chia đa thức A chia hết cho đa thức B.
- Giả sử \(\frac{A}{B} = Q + \frac{R}{B}\). Xác định m để \(\frac{R}{B}\) là số nguyên.
* Tìm các hệ số để đa thức A chia hết cho đa thức B
Cách 1. Nếu \(F\left( x \right)\) chia hết cho \(x - a\) thì \(F\left( a \right)\) là nghiệm.
Cách 2. Thực hiện phép chia đa thức dư R sao cho R = 0.
Bài tập
Bài 1: Để đa thức \(10{x^2} - 7x + a\) chia hết cho \(x - 2\) thì \(a\) bằng:
A. -26.
B. -12.
C. 24.
D. 12.
Bài 2: Để đa thức \(27{x^2} + a\) chia hết cho \(3x - 2\) thì \(a\) bằng:
A. -12.
B. 16.
C. 12.
D. 6.
Bài 3: Giá trị của m để đa thức \({x^3} - 2{x^2} + x + m\) chia hết cho đa thức \(x + 1\) là:
A. -3.
B. 2.
C. 4.
D. -1.
Bài 4: Nếu đa thức \(3{x^2} + mx + 27\) chia \(x + 5\) có số dư bằng 2 thì a bằng:
A. 10.
B. 20.
C. 15.
D. 51.
Bài 5: Cho hai đa thức \(F\left( x \right) = 6{x^3} - 7{x^2} - x + m\) và \(G\left( x \right) = 2x + 1\). Tìm giá trị của \(m\) để \(F\left( x \right)\) chia hết cho \(G\left( x \right)\).
Bài 6: Tìm m để đa thức \(A\left( x \right) = {x^3} - 3x + 5x + m\) chia hết cho đa thức \(B\left( x \right) = x - 2\).
Bài 7: Tìm giá trị nguyên của n để:
a) \(n + 3\) chia hết cho \(n\).
b) \(2n - 5\) chia hết cho \(n\).
Bài 8: Tìm giá trị nguyên của n để:
a) \({n^2} - 3n + 2\) chia hết cho \(n - 3\).
b) \(8{n^2} - 4n + 1\) chia hết cho \(2n + 1\).
Bài 9: Tìm giá trị nguyên của n để:
a) \(3{n^3} + 10{n^2} - 5\) chia hết cho \(3n + 1\).
b) \({n^3} + 3n - 5\) chia hết cho \({n^2} + 3\).
Bài 10: Xác định giá trị của a sao cho:
a) \(4x + a\) chia hết cho \(2x + 1\).
b) \({x^2} - ax + 3\) chia hết cho \(x - 3\).
Bài 11: Xác định hằng số a sao cho:
a) \(6{x^2} - ax - 7\) chia hết cho \(x + 1\).
b) \(10{x^2} - 7x + a\) chia hết cho \(2x - 3\).
--------Hết--------
Lời giải chi tiết:
Bài 1: Để đa thức \(10{x^2} - 7x + a\) chia hết cho \(x - 2\) thì \(a\) bằng:
A. -26.
B. -12.
C. 24.
D. 12.
Phương pháp
Chia \(10{x^2} - 7x + a\) cho \(x - 2\).
\(10{x^2} - 7x + a\) chia hết cho \(x - 2\) thì số dư bằng 0. Thay số dư bằng 0 để tìm a.
Lời giải

Số dư của phép chia là \(a + 26\).
Để đa thức \(10{x^2} - 7x + a\) chia hết cho \(x - 2\) thì \(a + 26 = 0\), suy ra \(a = - 26\).
Đáp án: A
Bài 2: Để đa thức \(27{x^2} + a\) chia hết cho \(3x - 2\) thì \(a\) bằng:
A. -12.
B. 16.
C. 12.
D. 6.
Phương pháp
Chia \(27{x^2} + a\) cho \(3x - 2\).
\(27{x^2} + a\) chia hết cho \(3x - 2\) thì số dư bằng 0. Thay số dư bằng 0 để tìm a.
Lời giải

Số dư của phép chia là \(a + 12\).
Để đa thức \(27{x^2} + a\) chia hết cho \(3x - 2\) thì \(a + 12 = 0\), suy ra \(a = - 12\).
Đáp án: A
Bài 3: Giá trị của m để đa thức \({x^3} - 2{x^2} + x + m\) chia hết cho đa thức \(x + 1\) là:
A. -3.
B. 2.
C. 4.
D. -1.
Phương pháp
Chia \({x^3} - 2{x^2} + x + m\) cho \(x + 1\).
\({x^3} - 2{x^2} + x + m\) chia hết cho \(x + 1\) thì số dư bằng 0. Thay số dư bằng 0 để tìm m.
Lời giải

Để đa thức \({x^3} - 2{x^2} + x + m\) chia hết cho \(x + 1\) thì \(m - 4 = 0\) suy ra \(m = 4\).
Đáp án: C
Bài 4: Nếu đa thức \(3{x^2} + mx + 27\) chia \(x + 5\) có số dư bằng 2 thì a bằng:
A. 10.
B. 20.
C. 15.
D. 51.
Phương pháp
Chia \(3{x^2} + ax + 27\) cho \(x + 5\), xác định số dư.
Từ số dư bằng 2 để tìm a.
Lời giải

Số dư của phép chia là \( - 5a + 102\).
Để đa thức \(3{x^2} + ax + 27\) chia \(x + 5\) có số dư bằng 2 thì
\(\begin{array}{l} - 5a + 102 = 2\\ - 5a = - 100\\a = 20\end{array}\)
Đáp án: B
Bài 5: Cho hai đa thức \(F\left( x \right) = 6{x^3} - 7{x^2} - x + m\) và \(G\left( x \right) = 2x + 1\). Tìm giá trị của \(m\) để \(F\left( x \right)\) chia hết cho \(G\left( x \right)\).
Phương pháp
Chia \(F\left( x \right)\) cho \(G\left( x \right)\).
\(F\left( x \right)\) chia hết cho \(G\left( x \right)\) thì số dư bằng 0. Thay số dư bằng 0 để tìm m.
Lời giải
Thực hiện phép chia \(F\left( x \right)\) cho \(G\left( x \right)\), ta được:
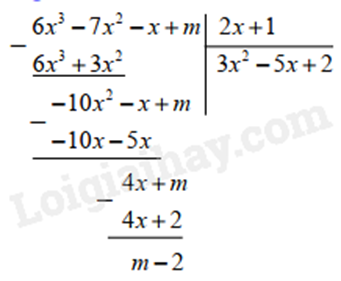
Để \(F\left( x \right)\) chia hết cho \(G\left( x \right)\) thì \(m - 2 = 0\) hay \(m = 2\).
Bài 6: Tìm m để đa thức \(A\left( x \right) = {x^3} - 3x + 5x + m\) chia hết cho đa thức \(B\left( x \right) = x - 2\).
Phương pháp
Thực hiện chia đa thức cho đa thức.
Đa thức chia hết cho đa thức thì số dư bằng 0. Thay số dư bằng 0 để tìm a.
Lời giải
Ta có:

\(A\left( x \right) \vdots B\left( x \right)\) khi \(m + 6 = 0\), suy ra \(m = - 6\).
Bài 7: Tìm giá trị nguyên của n để:
a) \(n + 3\) chia hết cho \(n\).
b) \(2n - 5\) chia hết cho \(n\).
Phương pháp
- Thực hiện phép chia đa thức A chia hết cho đơn thức B.
- Giả sử \(\frac{A}{B} = Q + \frac{R}{B}\). Xác định n để \(\frac{R}{B}\) là số nguyên.
Lời giải
a) Do \(\frac{{n + 3}}{n} = 1 + \frac{3}{n}\) nên để \(n + 3\) chia hết cho \(n\) thì \(3\) chia hết cho \(n\).
Suy ra n là ước của 3 = \(\left\{ {1;3; - 1; - 3} \right\}\).
Vậy \(n \in \left\{ {1;3; - 1; - 3} \right\}\).
b) Do \(\frac{{2n - 5}}{n} = \frac{{2n}}{n} - \frac{5}{n} = 2 - \frac{5}{n}\) nên để \(2n - 5\) chia hết cho \(n\) thì \(5\) chia hết cho \(n\).
Suy ra n là ước của 5 = \(\left\{ {1;5; - 1; - 5} \right\}\).
Vậy \(n \in \left\{ {1;5; - 1; - 5} \right\}\).
Bài 8: Tìm giá trị nguyên của n để:
a) \({n^2} - 3n + 2\) chia hết cho \(n - 3\).
b) \(8{n^2} - 4n + 1\) chia hết cho \(2n + 1\).
Phương pháp
- Thực hiện phép chia đa thức A chia hết cho đa thức B.
- Giả sử \(\frac{A}{B} = Q + \frac{R}{B}\). Xác định n để \(\frac{R}{B}\) là số nguyên.
Lời giải
a) Do \(\frac{{{n^2} - 3n + 2}}{{n - 3}} = \frac{{n\left( {n - 3} \right) + 2}}{{n - 3}} = n + \frac{2}{{n - 3}}\) nên để \({n^2} - 3n + 2\) chia hết cho \(n - 3\) thì \(2\) chia hết cho \(n - 3\).
Suy ra (n – 3) là ước của 2 = \(\left\{ { - 2; - 1;1;2} \right\}\).
Ta có bảng giá trị sau:

Vậy \(n \in \left\{ {1;2;4;5} \right\}\).
b) Ta có:
\(\begin{array}{l}\frac{{8{n^2} - 4n + 1}}{{2n + 1}}\\ = \frac{{8{n^2} + 4{n^2} - 8n - 4 + 5}}{{2n + 1}}\\ = \frac{{4n\left( {2n + 1} \right) - 4\left( {2n + 1} \right) + 5}}{{2n + 1}}\\ = 4n - 4 + \frac{5}{{2n + 1}}\end{array}\)
Suy ra để \(8{n^2} - 4n + 1\) chia hết cho \(2n + 1\) thì \(5\) chia hết cho \(2n + 1\).
Suy ra \(\left( {2n + 1} \right)\) là ước của 5 = \(\left\{ { - 5; - 1;1;5} \right\}\).
Ta có bảng giá trị sau:

Vậy \(n \in \left\{ { - 3; - 1;0;2} \right\}\).
Bài 9: Tìm giá trị nguyên của n để:
a) \(3{n^3} + 10{n^2} - 5\) chia hết cho \(3n + 1\).
b) \({n^3} + 3n - 5\) chia hết cho \({n^2} + 3\).
Phương pháp
- Thực hiện phép chia đa thức A chia hết cho đa thức B.
- Giả sử \(\frac{A}{B} = Q + \frac{R}{B}\). Xác định n để \(\frac{R}{B}\) là số nguyên.
Lời giải
a) Thực hiện phép chia ta được: \(\frac{{3{n^3} + 10{n^2} - 5}}{{3n + 1}} = {n^2} + 3n - 1 - \frac{4}{{3n + 1}}\).
Nên để \(3{n^3} + 10{n^2} - 5\) chia hết cho \(3n + 1\) thì \(4\) chia hết cho \(3n + 1\).
Suy ra \(\left( {3n + 1} \right) \in \)Ư(4) = \(\left\{ { - 4; - 2; - 1;1;2;4} \right\}\).
Ta có bảng sau:

Vậy \(n \in \left\{ { - 1;0;1} \right\}\)
b) Thực hiện phép chia ta được: \(\frac{{{n^3} + 3n - 5}}{{{n^2} + 3}} = n - \frac{5}{{{n^2} + 3}}\).
Nên để \({n^3} + 3n - 5\) chia hết cho \({n^2} + 3\) thì 5 chia hết cho \({n^2} + 3\).
Suy ra \(\left( {{n^2} + 3} \right) \in \)Ư(5) = \(\left\{ { - 5; - 1;1;5} \right\}\).
Ta có bảng sau:

Vậy không có giá trị nào của n thoả mãn yêu cầu đề bài.
Bài 10: Xác định giá trị của a sao cho:
a) \(4x + a\) chia hết cho \(2x + 1\).
b) \({x^2} - ax + 3\) chia hết cho \(x - 3\).
Phương pháp
Thực hiện chia đa thức cho đa thức.
Đa thức chia hết cho đa thức thì số dư bằng 0. Thay số dư bằng 0 để tìm a.
Lời giải
a) Ta có:
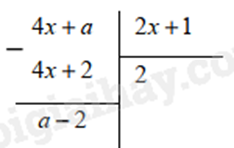
Để \(4x + a\) chia hết cho \(2x + 1\) thì \(a - 2 = 0\), suy ra \(a = 2\).
Vậy a = 2.
b) Ta có:

Để \({x^2} - ax + 3\) chia hết cho \(x - 3\) thì \(12 - 3a = 0\), suy ra \(a = \frac{{12}}{3} = 4\).
Vậy a = 4.
Bài 11: Xác định hằng số a sao cho:
a) \(6{x^2} - ax - 7\) chia hết cho \(x + 1\).
b) \(10{x^2} - 7x + a\) chia hết cho \(2x - 3\).
Phương pháp
Thực hiện chia đa thức cho đa thức.
Đa thức chia hết cho đa thức thì số dư bằng 0. Thay số dư bằng 0 để tìm a.
Lời giải
a) Ta có:
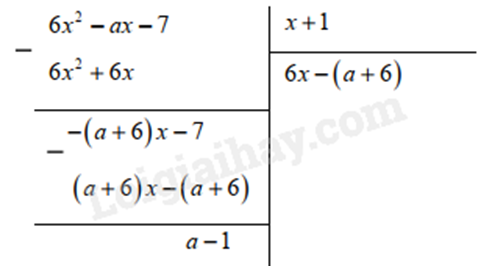
Để \(6{x^2} - ax - 7\) chia hết cho \(x + 1\) thì \(a - 1 = 0\), suy ra \(a = 1\).
Vậy \(a = 1\).
b) Ta có:

Để \(10{x^2} - 7x + a\) chia hết cho \(2x - 3\) thì \(a + 12 = 0\), suy ra \(a = - 12\).
Vậy \(a = - 12\).
Các bài khác cùng chuyên mục
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8











