Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8

Lý thuyết

* Định nghĩa:

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.

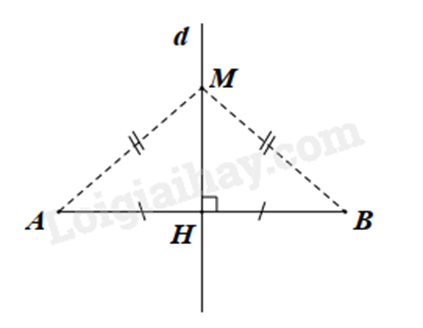
d là đường trung trực của đoạn AB.

Định lý 1: Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Định lý 2: Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

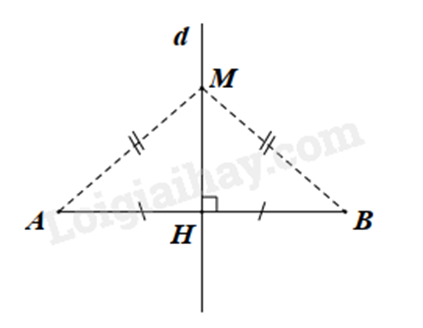
MA = MB thì M thuộc đường trung trực của đoạn AB.

* Nhận xét: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

Bài tập

Bài 1: Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.

A. trung trực.

B. giao điểm.

C. trọng tâm.

D. trung điểm.

Bài 2: Cho đoạn thẳng AB, điểm I là trung điểm của AB. Điểm M nằm trên đường trung trực của AB. Khẳng định nào sau đây là sai:

A. MA = MB.

B. \(MI \bot AB\).

C. \(\Delta AMI = \Delta IMB\).

D. \(\widehat {MAB} = \widehat {MBA}\).

Bài 3: Đường thẳng d là trung trực của đoạn thẳng MN khi

A. d đi qua điểm I của MN.

B. \(d \bot MN\).

C. \(d \bot MN\) tại I và IM = IN.

D. \(d//MN\) và IM = IN.

Bài 4: Cho \(\Delta ABC\) vuông tại A, AB < AC. Tia phân giác của \(\hat B\) cắt AC tại E. Từ E kẻ ED vuông góc với BC tại D. Kết luận nào sau đây đúng nhất?

A. \(\Delta ABE = \Delta DBE\).

B. \(\Delta BAD\) cân tại B.

C. BE là đường trung trực của đoạn thẳng AD.

D. Cả A, B, C đều đúng.

Bài 5: Cho \(\Delta ABC\) cân tại A có \(\widehat {CAB} = 50^\circ \), đường trung trực của AB cắt BC tại D. Tính \(\widehat {DAC}\).

A. \(15^\circ \).

B. \(30^\circ \).

C. \(50^\circ \).

D. \(60^\circ \).

Bài 6: Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì?

Bài 7: Cho \(\Delta ABC\) vuông tại A có \(\widehat {ACB} = 30^\circ \). Đường trung trực của BC cắt AC tại M. Chứng minh BM là tia phân giác của góc ABC.

Bài 8: Cho \(\Delta ABC\) có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE, AC cắt nhau tại O.

a) Chứng minh \(\Delta AOB = \Delta COE\).

b) Chứng minh AO là tia phân giác của \(\widehat {BAC}\).

Bài 9: Cho \(\Delta ABC\) có \(\widehat {BAC} = 100^\circ \). Các đường trung trực của AB và AC cắt BC lần lượt tại E và F. Tính \(\widehat {EAF}\).

Bài 10: Cho \(\Delta ABC\) vuông tại A, kẻ đường cao \(AH\). Trên cạnh AC lấy điểm K sao cho AK = AH. Kẻ \(KD \bot AC\) \(\left( {D \in BC} \right)\). Chứng minh rằng:

a) \(\Delta AHD = \Delta AKD\).

b) AD là đường trung trực của đoạn thẳng HK.

c) AD là tia phân giác của \(\widehat {HAK}\).

--------Hết--------

Lời giải chi tiết:

Bài 1: Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.

A. trung trực.

B. giao điểm.

C. trọng tâm.

D. trung điểm.

Phương pháp

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.

Lời giải

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Đáp án: D

Bài 2: Cho đoạn thẳng AB, điểm I là trung điểm của AB. Điểm M nằm trên đường trung trực của AB. Khẳng định nào sau đây là sai:

A. MA = MB.

B. \(MI \bot AB\).

C. \(\Delta AMI = \Delta IMB\).

D. \(\widehat {MAB} = \widehat {MBA}\).

Phương pháp

Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều 2 mút của đoạn thẳng đó.

Lời giải

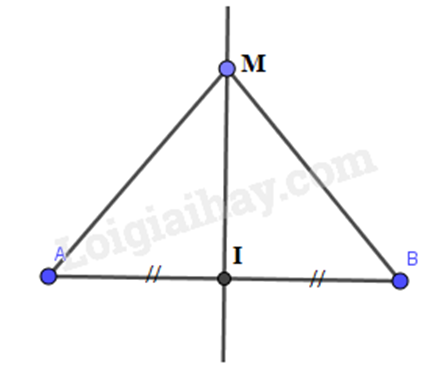
Vì M nằm trên đường trung trực của AB nên \(MI \bot AB\) và IA = IB

Vì M nằm trên đường trung trực của AB nên MA = MB (tính chất) nên A đúng

Do đó, tam giác MAB cân tại M

suy ra \(\widehat {MAB} = \widehat {MBA}\) nên D đúng

Xét \(\Delta AMI\) và \(\Delta BMI\), ta có:

MA = MB

MI chung

IA = IB

Suy ra \(\Delta AMI = \Delta BMI\) (c.c.c) nên C sai

Đáp án: C

Bài 3: Đường thẳng d là trung trực của đoạn thẳng MN khi

A. d đi qua điểm I của MN.

B. \(d \bot MN\).

C. \(d \bot MN\) tại I và IM = IN.

D. \(d//MN\) và IM = IN.

Phương pháp

Đường thẳng vuông góc với 1 đoạn thẳng tại trung điểm của nó là đường trung trực của đoạn thẳng đó.

Lời giải

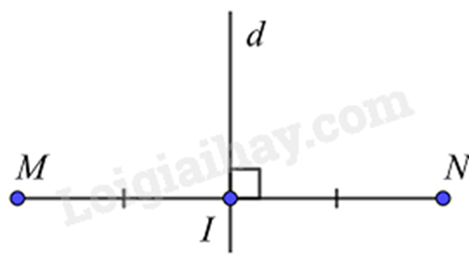
Đường thẳng d là trung trực của đoạn thẳng MN khi \(d \bot MN\) tại I và IM = IN.

Đáp án: C

Bài 4: Cho \(\Delta ABC\) vuông tại A, AB < AC. Tia phân giác của \(\hat B\) cắt AC tại E. Từ E kẻ ED vuông góc với BC tại D. Kết luận nào sau đây đúng nhất?

A. \(\Delta ABE = \Delta DBE\).

B. \(\Delta BAD\) cân tại B.

C. BE là đường trung trực của đoạn thẳng AD.

D. Cả A, B, C đều đúng.

Phương pháp

- Sử dụng trường hợp cạnh huyền - góc nhọn để chứng minh hai tam giác bằng nhau.

- Từ hai tam giác bằng nhau suy ra hai điểm cách đều hai mút của đoạn thẳng đó nên là đường trung trực.

- Tam giác có hai cạnh bằng nhau là tam giác cân.

Lời giải

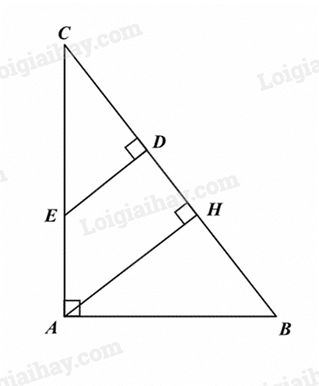
Xét \(\Delta ABE\) và \(\Delta DBE\) có:

BE là cạnh chung.

\(\widehat {ABE} = \widehat {DBE}\) (BE là phân giác của \(\hat B\))

\(\widehat {BAE} = \widehat {BDE} = 90^\circ \)

Do đó \(\Delta ABE = \Delta DBE\) (cạnh huyền – góc nhọn)

Vì vậy đáp án A đúng.

Ta có \(\Delta ABE = \Delta DBE\) (chứng minh trên)

Suy ra BA = BD và AE = DE (các cặp cạnh tương ứng)

Vì vậy BE là đường trung trực của đoạn thẳng AD.

Do đó đáp án C đúng.

Vì BA = BD nên \(\Delta BAD\) cân tại B.

Vì vậy đáp án B đúng.

Vậy ta chọn đáp án D.

Đáp án: D

Bài 5: Cho \(\Delta ABC\) cân tại A có \(\widehat {CAB} = 50^\circ \), đường trung trực của AB cắt BC tại D. Tính \(\widehat {DAC}\).

A. \(15^\circ \).

B. \(30^\circ \).

C. \(50^\circ \).

D. \(60^\circ \).

Phương pháp

Áp dụng tính chất tam giác cân để tính \(\widehat {ABC}\).

Sử dụng tính chất đường trung trực suy ra \(\Delta ABD\) cân tại D, suy ra \(\widehat {ABD} = \widehat {BAD}\), ta có \(\widehat {BAD}\).

Sử dụng trừ góc để tính góc \(\widehat {CAD}\).

Lời giải

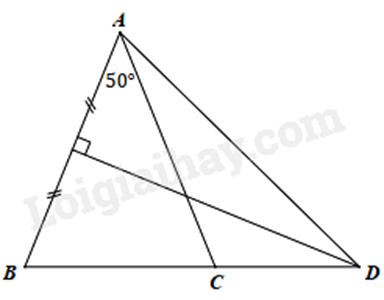
Vì \(\Delta ABC\) cân tại A (gt) nên \(\widehat {ABC} = \frac{{180^\circ  - \widehat {BAC}}}{2} = \frac{{180^\circ  - 50^\circ }}{2} = 65^\circ \) (tính chất tam giác cân)

Vì D thuộc đường trung trực của đoạn thẳng AB nên AD = BD (tính chất đường trung trực), suy ra \(\Delta ABD\) cân tại D.

Suy ra \(\widehat {ABD} = \widehat {BAD}\) (tính chất tam giác cân).

Mà \(\widehat {ABD} = 65^\circ \) (cmt) nên \(\widehat {BAD} = 65^\circ \).

Mà \(\widehat {CAB} + \widehat {CAD} = \widehat {BAD}\)

nên \(50^\circ  + \widehat {CAD} = 65^\circ \)

Suy ra \(\widehat {CAD} = 65^\circ  - 50^\circ  = 15^\circ \).

Đáp án: A

Bài 6: Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì?

Phương pháp

Sử dụng tính chất đường trung trực của đoạn thẳng.

Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.

Lời giải

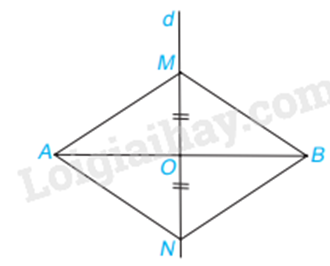
Vì M nằm trên đường trung trực của AB nên MA = MB (tính chất)

Vì N nằm trên đường trung trực của AB nên NA = NB (tính chất)

Xét tam giác AOM và AON có:

OM = ON

\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)

AO chung

Do đó \(\Delta AOM = \Delta AON\) (c.g.c)

nên AM = AN (2 cạnh tương ứng)

Mà MA = MB; NA = NB

Suy ra MA = MB = NB = NA

Do đó tứ giác AMBN là hình thoi (tứ giác có 4 cạnh bằng nhau)

Bài 7: Cho \(\Delta ABC\) vuông tại A có \(\widehat {ACB} = 30^\circ \). Đường trung trực của BC cắt AC tại M. Chứng minh BM là tia phân giác của góc ABC.

Phương pháp

Sử dụng tính chất đường trung trực, chứng minh \(\Delta BMC\) cân tại M.

Suy ra \(\widehat {MBC}\).

Áp dụng tính chất tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ \), tính \(\widehat {CBA}\).

Chứng minh \(\widehat {MBC} = \frac{{\widehat {CBA}}}{2}\) nên BM là tia phân giác của \(\widehat {ABC}\).

Lời giải

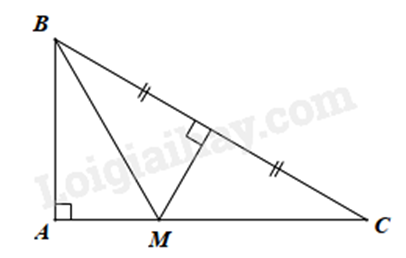
Vì M thuộc đường trung trực của BC nên BM = CM (tính chất đường trung trực), suy ra \(\Delta BMC\) cân tại M.

Do đó \(\widehat {MBC} = \widehat {BCM}\) (tính chất tam giác cân).

Mà \(\widehat {BCM} = 30^\circ \) (gt) nên \(\widehat {MBC} = 30^\circ \) (1)

Xét \(\Delta ABC\) có \(\widehat A = 90^\circ \) nên \(\widehat {BCA} + \widehat {CBA} = 90^\circ \)

\(30^\circ  + \widehat {CBA} = 90^\circ \) nên \(\widehat {CBA} = 90^\circ  - 30^\circ  = 60^\circ \) (2)

Từ (1) và (2) suy ra \(\widehat {CBM} = \frac{{\widehat {CBA}}}{2}\) nên BM là tia phân giác của \(\widehat {ABC}\).

Bài 8: Cho \(\Delta ABC\) có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE, AC cắt nhau tại O.

a) Chứng minh \(\Delta AOB = \Delta COE\).

b) Chứng minh AO là tia phân giác của \(\widehat {BAC}\).

Phương pháp

a) Sử dụng tính chất đường trung trực của đoạn thẳng để suy ra các cạnh bằng nhau.

Chứng minh \(\Delta AOB = \Delta COE\) theo trường hợp cạnh – cạnh – cạnh.

b) Chứng minh \(\widehat {BAO} = \widehat {ECO}\) và \(\widehat {CAO} = \widehat {ECO}\) nên \(\widehat {CAO} = \widehat {BAO}\), suy ra AO là tia phân giác của \(\widehat {BAC}\).

Lời giải

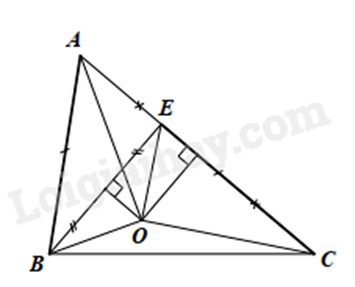
a) Ta có: O thuộc đường trung trực của BE (gt) nên OB = OE (tính chất đường trung trực)

               O thuộc đường trung trực của AC (gt) nên OC = OA (tính chất đường trung trực).

Xét \(\Delta AOB\) và \(\Delta COE\) có:

AO = CO (cmt)

OB = OE (cmt)

AB = CE (gt)

Suy ra \(\Delta AOB = \Delta COE\) (c.c.c).

b) Từ \(\Delta AOB = \Delta COE\) (cmt) suy ra \(\widehat {BAO} = \widehat {ECO}\) (hai góc tương ứng) (1)

Vì OC = OA nên \(\Delta AOC\) cân tại O, suy ra \(\widehat {CAO} = \widehat {ECO}\) (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra \(\widehat {CAO} = \widehat {BAO}\left( { = \widehat {ECO}} \right)\).

Do đó AO là tia phân giác của \(\widehat {BAC}\).

Bài 9: Cho \(\Delta ABC\) có \(\widehat {BAC} = 100^\circ \). Các đường trung trực của AB và AC cắt BC lần lượt tại E và F. Tính \(\widehat {EAF}\).

Phương pháp

Sử dung tính chất đường trung trực chứng minh \(\Delta AEB\) cân tại E, do đó \(\widehat {EAB} = \widehat {EBA}\) (tính chất tam giác cân)

Chứng minh tương tự, ta có \(\Delta AFC\) cân tại F nên \(\widehat {FAC} = \widehat {FCA}\) (tính chất tam giác cân)

Áp dụng định lí tổng ba góc trong tam giác bằng \(180^\circ \) vào tam giác ABC để tính \(\widehat {ABC} + \widehat {ACB}\).

Kết hợp với \(\widehat {BAC} = \widehat {BAE} + \widehat {EAF} + \widehat {FAC}\) để tính \(\widehat {EAF}\).

Lời giải

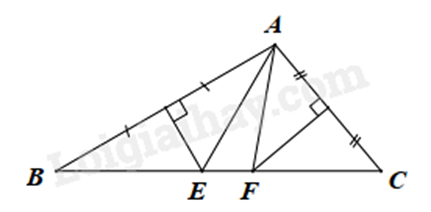
Vì E thuộc đường trung trực của AB (gt) nên AE = BE (tính chất đường trung trực)

Suy ra \(\Delta AEB\) cân tại E, do đó \(\widehat {EAB} = \widehat {EBA}\) (tính chất tam giác cân)

Chứng minh tương tự, ta có \(\Delta AFC\) cân tại F nên \(\widehat {FAC} = \widehat {FCA}\) (tính chất tam giác cân)

Xét \(\Delta ABC\) có: \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \) (tổng ba góc trong tam giác)

\(100^\circ  + \widehat {ABC} + \widehat {ACB} = 180^\circ \)

Suy ra \(\widehat {ABC} + \widehat {ACB} = 180^\circ  - 100^\circ  = 80^\circ \)

Mà \(\widehat {BAC} = \widehat {BAE} + \widehat {EAF} + \widehat {FAC}\); \(\widehat {EAB} = \widehat {EBA}\) (cmt) và \(\widehat {FAC} = \widehat {FCA}\)  (cmt)

nên \(\widehat {EAF} = 180^\circ  - 2\left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ  - 2.80^\circ  = 20^\circ \).

Vậy \(\widehat {EAF} = 20^\circ \).

Bài 10: Cho \(\Delta ABC\) vuông tại A, kẻ đường cao \(AH\). Trên cạnh AC lấy điểm K sao cho AK = AH. Kẻ \(KD \bot AC\) \(\left( {D \in BC} \right)\). Chứng minh rằng:

a) \(\Delta AHD = \Delta AKD\).

b) AD là đường trung trực của đoạn thẳng HK.

c) AD là tia phân giác của \(\widehat {HAK}\).

Phương pháp

a) Chứng minh \(\Delta AHD = \Delta AKD\) theo trường hợp cạnh huyền – cạnh góc vuông.

b) Chứng minh HD = KD nên D thuộc đường trung trực của đoạn thẳng HK.

Chứng minh AH = AK nên A thuộc đường trung trực của đoạn thẳng HK.

Suy ra AH là đường trung trực của đoạn thẳng HK.

c) Chứng minh \(\widehat {HAD} = \widehat {KAD}\) nên AD là tia phân giác của \(\widehat {HAK}\).

Lời giải

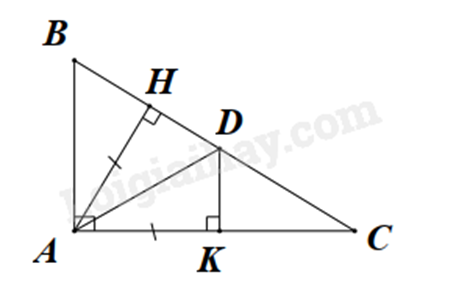
a) Vì AH là đường cao của \(\Delta ABC\) (gt) nên \(AH \bot BC\), suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ \).

Vì \(KD \bot AC\) \(\left( {D \in BC} \right)\) (gt) nên \(\widehat {AKD} = \widehat {DKC} = 90^\circ \).

Xét \(\Delta AHD\left( {\widehat H = 90^\circ } \right)\) và \(\Delta AKD\left( {\widehat K = 90^\circ } \right)\) có:

AH = AK (gt)

AD chung

nên \(\Delta AHD = \Delta AKD\) (ch – cgv).

b) Vì \(\Delta AHD = \Delta AKD\) (cmt) nên HD = KD (hai cạnh tương ứng) nên D thuộc đường trung trực của đoạn thẳng HK.

Mà AH = AK nên A thuộc đường trung trực của đoạn thẳng HK.

Do đó AH là đường trung trực của đoạn thẳng HK.

c) Vì \(\Delta AHD = \Delta AKD\) (cmt) nên \(\widehat {HAD} = \widehat {KAD}\) (hai góc tương ứng)

Do đó AD là tia phân giác của \(\widehat {HAK}\).