Dạng bài đường vuông góc và đường xiên - Ôn hè Toán 7 lên 8

Lý thuyết

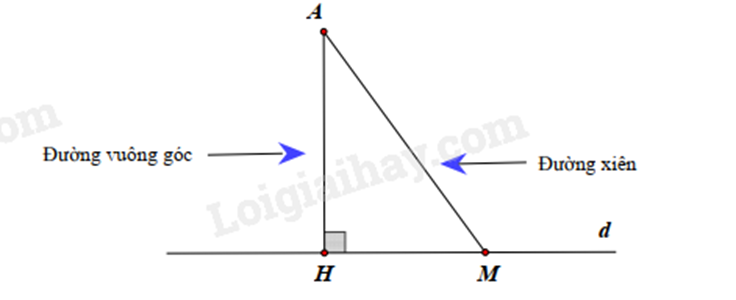
* Quan hệ giữa đường vuông góc và đường xiên:

Định lí 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở bên ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.

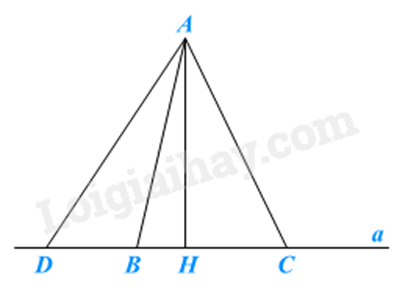
\(AH \bot a\) nên AH < AD, AH < AB, AH < AC.

* Quan hệ giữa đường xiên và hình chiếu:

Định lí 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

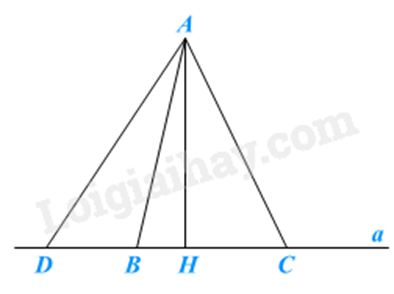
+ \(AH \bot a\), \(HD > HB\) nên \(AD > AB\)

+ \(AH \bot a\), \(AD > AB\) nên \(HD > HB\).

+ \(AD = AC\) khi và chỉ khi \(HD = HC\).

Bài tập

Bài 1: Cho ba điểm \(A,{\mkern 1mu} B,{\mkern 1mu} C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với AC tại \(B\) ta lấy điểm \(H\). Khi đó

A. \(AH < BH\).

B. \(AH < AB\).

C. \(AH > BH\).

D. \(AH = BH\).

Bài 2: Em hãy chọn cụm từ thích hợp điền vào chỗ trống:

“Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì…”

A. lớn hơn.

B. ngắn hơn.

C. nhỏ hơn.

D. bằng nhau.

Bài 3: Trong tam giác ABC có \(AH \bot BC\left( {H \in BC} \right)\). Chọn câu sai.

A. Nếu AB < AC thì BH < HC.

B. Nếu AB > AC thì BH < HC.

C. Nếu AB = AC thì BH = HC.

D. Nếu HB > HC thì AB > AC.

Bài 4: Cho hình vẽ sau:

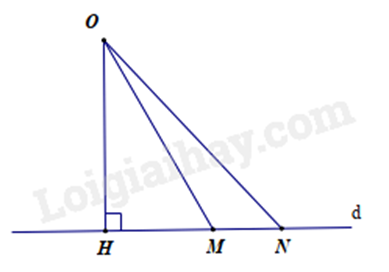
A. OM > OH.

B. ON > OH.

C. ON > OM.

D. \(\widehat {OMN} < \widehat {MNO}\).

Bài 5: Cho hình vẽ sau:

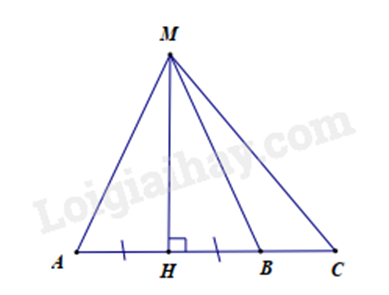
Em hãy chọn đáp án sai trong các đáp án sau:

A. MA > MH.

B. HB < HC.

C. MA = MB.

D. MC < MA.

Bài 6: Cho \(\Delta MNP\) vuông tại M. Trên tia đối của tia NM lấy điểm D.

a) So sánh PN và PD.

b) Lấy điểm E trên cạnh MP. Chứng minh EN < PD.

Bài 7: Cho \(\Delta ABC\) vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của \(A\) và \(C\) xuống đường thẳng BM. So sánh \(BD + BE\) và AB.

Bài 8: Cho \(\Delta ABC\) có CE  và BD  là hai đường cao. So sánh BD + CE và AB + AC?

Bài 9: Cho \(\Delta ABC\) có \(\hat C = 90^\circ \), \(AC < BC\) , kẻ \(CH \bot AB\). Trên các cạnh AB và AC lấy tương ứng hai điểm \(M\) và \(N\) sao cho \(BM = BC,CN = CH\).

a) Chứng minh \(MN \bot AC\).

b) So sánh AC + BC và AB + CH.

Bài 10: Cho góc \(\widehat {xOy} = 60^\circ \), \(A\) là điểm trên tia \(Ox\), \(B\) là điểm trên tia Oy \((A,B\) không trùng với \(O).\) Chứng minh rằng \(OA + OB \le 2AB\). Biết rằng trong tam giác vuông, cạnh đối diện với góc \(30^\circ \) bằng nửa cạnh huyền.

--------Hết--------

Lời giải chi tiết:

Bài 1: Cho ba điểm \(A,{\mkern 1mu} B,{\mkern 1mu} C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với AC tại \(B\) ta lấy điểm \(H\). Khi đó

A. \(AH < BH\).

B. \(AH < AB\).

C. \(AH > BH\).

D. \(AH = BH\).

Phương pháp

Áp dụng định lí quan hệ đường vuông góc với đường xiên.

Lời giải

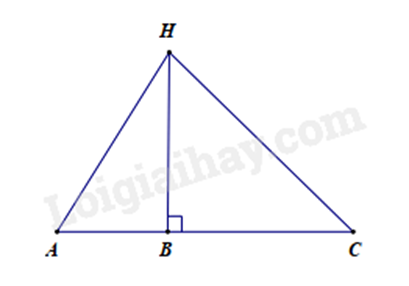
Vì BH là đường vuông góc và AH là đường xiên nên \(AH > BH.\)

Đáp án: C

Bài 2: Em hãy chọn cụm từ thích hợp điền vào chỗ trống:

“Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì…”

A. lớn hơn.

B. ngắn hơn.

C. nhỏ hơn.

D. bằng nhau.

Phương pháp

Áp dụng định lí về quan hệ giữa đường xiên và hình chiếu.

Lời giải

Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.

Đáp án: C

Bài 3: Trong tam giác ABC có \(AH \bot BC\left( {H \in BC} \right)\). Chọn câu sai.

A. Nếu AB < AC thì BH < HC.

B. Nếu AB > AC thì BH < HC.

C. Nếu AB = AC thì BH = HC.

D. Nếu HB > HC thì AB > AC.

Phương pháp

Sử dụng mối quan hệ giữa giữa đường xiên và hình chiếu.

Lời giải

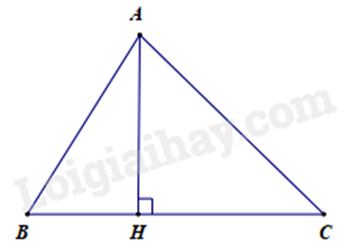
Trong tam giác ABC có AH là đường vuông góc và BH, CH là hai hình chiếu.

Khi đó

+ Nếu AB < AC thì BH < HC (A đúng)

+ Nếu AB > AC thì BH < HC (B sai)

+ Nếu AB = AC thì BH = HC (C đúng)

+ Nếu HB > HC thì ÂB > AC (D đúng)

Đáp án: B

Bài 4: Cho hình vẽ sau:

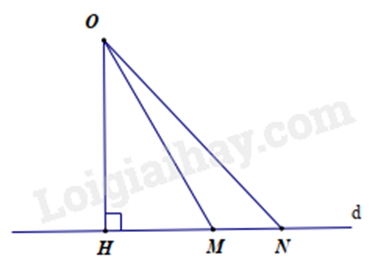
A. OM > OH.

B. ON > OH.

C. ON > OM.

D. \(\widehat {OMN} < \widehat {MNO}\).

Phương pháp

Áp dụng:
+ Định lí về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
+ Tính chất: Trong tam giác tù, góc tù là góc lớn nhất.

Lời giải

Vì OH là đường vuông góc và OM, ON là đường xiên nên OH < OM; OH < ON (quan hệ giữa đường vuông góc và đường xiên).

Đáp án A, B đúng nên loại A, B.

Vì M nằm giữa hai điểm H và N nên HM < HN suy ra OM < ON (quan hệ giữa đường xiên và hình chiếu).

Đáp án C đúng nên loại C.

Xét \(\Delta OHM\) vuông tại H nên \(\widehat {HMO}\) là góc nhọn hay \(\widehat {HMO} < 90^\circ \).

Mặt khác \(\widehat {HMO} + \widehat {OMN} = 180^\circ \) (hai góc kề bù)

nên \(\widehat {OMN} > 180^\circ  - 90^\circ \)

suy ra \(\widehat {OMN} > 90^\circ \) hay \(\widehat {OMN}\) là góc tù. Do đó \(\widehat {OMN} > \widehat {MNO}\). Do đó đáp án D sai.

Đáp án: D

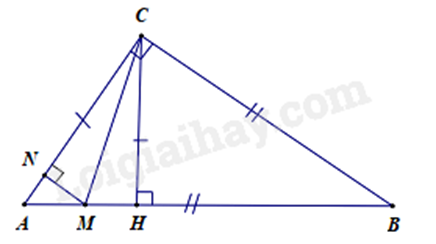
Bài 5: Cho hình vẽ sau:

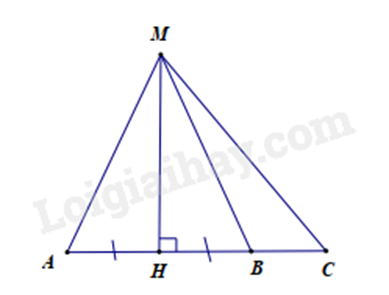
Em hãy chọn đáp án sai trong các đáp án sau:

A. MA > MH.

B. HB < HC.

C. MA = MB.

D. MC < MA.

Phương pháp

Áp dụng các định lí sau:
+ Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
+ Quan hệ giữa góc và cạnh trong tam giác.

Lời giải

Vì MH là đường vuông góc và MA là đường xiên nên MA > MH (quan hệ đường vuông góc và đường xiên)

Đáp án A đúng nên loại A.

Vì \(\widehat {MBC}\) là góc ngoài của \(\Delta MHB\) nên \(\widehat {MBC} = \widehat {MHB} + \widehat {BMH} > \widehat {MHB} = 90^\circ \)

Xét \(\Delta MBC\) có \(\widehat {MBC}\) là góc tù nên suy ra \(MC > MB\) (quan hệ giữa góc và cạnh trong tam giác).

Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC, do đó HB < HC (quan hệ giữa đường xiên và hình chiếu.

Đáp án B đúng nên loại B.

Vì AH = HB (gt). Mà AH và HB lần lượt là hình chiếu của AM và BM nên MA = MB (quan hệ giữa đường xiên và hình chiếu.

Đáp án C đúng nên loại đáp án C.

Vì MB = MA, MC > MB nên MC > MA.

Vậy đáp án D sai.

Đáp án: D

Bài 6: Cho \(\Delta MNP\) vuông tại M. Trên tia đối của tia NM lấy điểm D.

a) So sánh PN và PD.

b) Lấy điểm E trên cạnh MP. Chứng minh EN < PD.

Phương pháp

Sử dụng định lí quan hệ giữa đường xiên và hình chiếu.

Lời giải

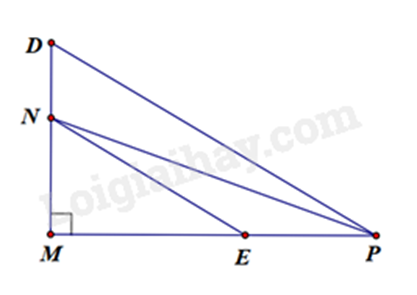
a) Từ giả thiết, ta có: MN < MD

Mà MN, MD lần lượt là hình chiếu của PN, PD lên đường thẳng MD

Do đó: PN < PD.

b) Ta có: ME < MP.

Mà ME, MP lần lượt là hình chiếu của NE, NP lên đường thẳng MP.

Do đó: NE < NP.

Mà PN < PD nên NE < PD.

Bài 7: Cho \(\Delta ABC\) vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của \(A\) và \(C\) xuống đường thẳng BM. So sánh \(BD + BE\) và AB.

Phương pháp

- Sử dụng quan hệ giữa đường vuông góc với đường xiên

- Sử dụng tính chất của trung điểm

- Chứng minh \(\Delta ADM = \Delta CEM\) (ch - gn)

Lời giải

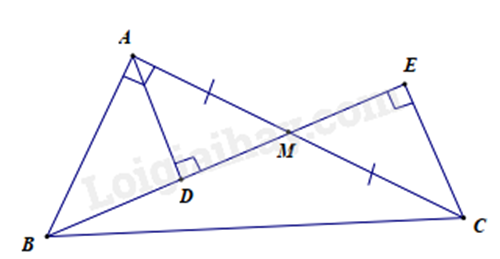
Vì \(\Delta ABM\) vuông tại \(A\)  (gt) nên \(BA < BM\) (quan hệ giữa đường vuông góc và đường xiên).

Mà \(BM = BD + DM\) nên \(BA < BD + DM\left( 1 \right)\) .

Mặt khác, \(BM = BE - ME\) nên \(BA < BE - ME\left( 2 \right)\)

Cộng hai vế của \(\left( 1 \right)\)và \(\left( 2 \right)\) ta được: \(2BA < BD + BE + MD - ME\left( 3 \right)\)

Vì \(M\)  là trung điểm của AC (gt) nên AM = MC (tính chất trung điểm)

Xét tam giác vuông ADM  và tam giác vuông CEM  có:

\(AM = MC\left( {cmt} \right)\)

\(\widehat {AMD} = \widehat {EMC}\) (đối đỉnh)

nên \(\Delta ADM = \Delta CEM\) (cạnh huyền – góc nhọn)

suy ra \(MD = ME\left( 4 \right)\) (2 cạnh tương ứng)

Từ \(\left( 3 \right)\)và \(\left( 4 \right)\) suy ra \(BD + BE > 2AB\)

Bài 8: Cho \(\Delta ABC\) có CE  và BD  là hai đường cao. So sánh BD + CE và AB + AC?

Phương pháp

Chứng minh CE và BD là đường vuông góc, AC và AB là đường xiên.

Sử dụng định lí về đường vuông góc và đường xiên để so sánh.

Lời giải

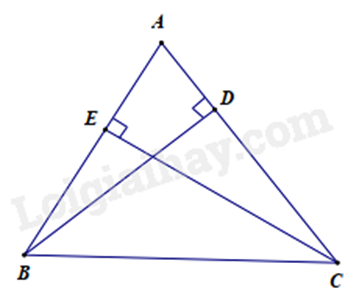
Vì \(BD \bot AC\left( {gt} \right)\) và \(EC \bot AB\left( {gt} \right)\) nên BD  và CE  là lần lượt là hai đường vuông góc của hai đường xiên AC  và AB.

Suy ra BD < AB và EC < AC (đường vuông góc nhỏ hơn đường xiên)

Dp đó BD + EC < AB + AC

Bài 9: Cho \(\Delta ABC\) có \(\hat C = 90^\circ \), \(AC < BC\) , kẻ \(CH \bot AB\). Trên các cạnh AB và AC lấy tương ứng hai điểm \(M\) và \(N\) sao cho \(BM = BC,CN = CH\).

a) Chứng minh \(MN \bot AC\).

b) So sánh AC + BC và AB + CH.

Phương pháp

a) Áp dụng tính chất tam giác cân.

b)  Áp dụng quan hệ đường vuông góc và đường xiên.

Lời giải

a) Ta có: \(BM = BC\left( {gt} \right)\) nên \(\Delta BMC\) cân tại \(B\) (dấu hiệu nhận biết tam giác cân)

 suy ra \(\widehat {MCB} = \widehat {CMB}\left( 1 \right)\) (tính chất tam giác cân)

Lại có: \(\widehat {BCM} + \widehat {MCA} = \widehat {ACB} = 90^\circ \left( {gt} \right)\) và \(\widehat {CMH} + \widehat {MCH} = 90^\circ \left( {gt} \right)\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {MCH} = \widehat {MCN}\)

Xét \(\Delta MHC\) và \(\Delta MNC\) có:

MC  chung

\(\widehat {MCH} = \widehat {MCN}\left( {cmt} \right)\)

\(NC = HC\left( {gt} \right)\)

suy ra \(\Delta MHC = \Delta MNC\left( {c.g.c} \right)\), do đó \(\widehat {MNC} = \widehat {MHC} = 90^\circ \) (2 góc tương ứng) hay \(MN \bot AC\).

b) Xét \(\Delta AMN\) có AN  là đường vuông góc hạ từ \(A\)  xuống MN  và AM  là đường xiên nên suy ra \(AM > AN\) (quan hệ đường vuông góc và đường xiên)

Ta có: BM = BC (gt), HC = CN (gt) và AM > AN (cmt), do đó:

\(BM + MA + HC > BC + CN + NA\)

hay \(AB + HC > BC + AC\).

Bài 10: Cho góc \(\widehat {xOy} = 60^\circ \), \(A\) là điểm trên tia \(Ox\), \(B\) là điểm trên tia Oy \((A,B\) không trùng với \(O).\) Chứng minh rằng \(OA + OB \le 2AB\). Biết rằng trong tam giác vuông, cạnh đối diện với góc \(30^\circ \) bằng nửa cạnh huyền.

Phương pháp

Kẻ tia phân giác Ot của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{60^\circ }}{2} = 30^\circ .\)

Gọi \(I\) là giao của Ot và AB. Kẻ \(AH \bot Ot,BK \bot Ot\)

Xét \(\Delta OAH\) có \(\widehat {AOH} = 30^\circ \) nên \(OA = 2AH.\) Từ đó so sánh OA và AI (1)

Xét \(\Delta OBK\) có \(\widehat {BOK} = 30^\circ \) nên \(OB = 2BK.\) Từ đó so sánh OB và BI    (2)

Từ (1) và (2) ta so sánh được \(OA + OB\) với 2AB.

* Chú ý: Trong tam giác vuông, cạnh đối diện với góc \(30^\circ \) bằng nửa cạnh huyền.

Lời giải

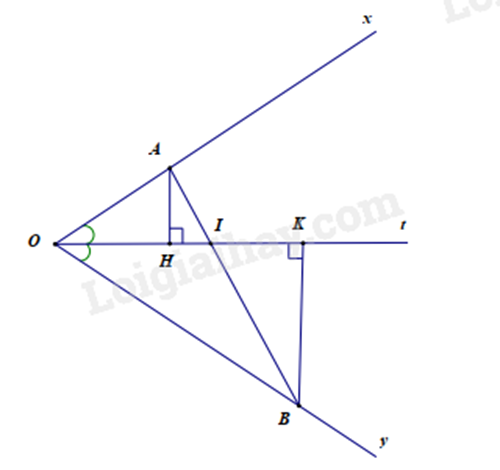
Kẻ tia phân giác Ot của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{60^\circ }}{2} = 30^\circ .\)

Gọi \(I\) là giao của Ot và AB. Kẻ \(AH \bot Ot,BK \bot Ot\).

Xét \(\Delta OAH\) có \(\widehat {AOH} = 30^\circ \) nên \(OA = 2AH.\)

Vì \(AH,{\mkern 1mu} AI\) lần lượt là đường vuông góc, đường xiên kẻ từ \(A\) đến Ot nên \(AH \le AI\) do đó \(OA \le 2AI\)    (1)

Xét \(\Delta OBK\) có \(\widehat {BOK} = 30^\circ \) nên \(OB = 2BK.\)

Vì \(BK,{\mkern 1mu} BI\) lần lượt là đường vuông góc, đường xiên kẻ từ \(B\) đến Ot nên \(BK \le BI\) do đó \(OB \le 2BI\)    (2)

Cộng (1) với (2) theo vế với vế ta được:

\(\begin{array}{l}OA + OB \le 2AI + 2BI\\OA + OB \le 2\left( {AI + BI} \right)\\OA + OB \le 2AB\end{array}\)

Vậy \(OA + OB \le 2AB\).