Đề ôn hè Toán 7 lên 8 - Đề 7

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Số nguyên \(n\) thỏa mãn đẳng thức \({\left( {\frac{8}{{27}}} \right)^n} = {\left( {\frac{2}{3}} \right)^{12}}\) là

A. \(n = 12\).

B. \(n = 8\).

C. \(n = 4\).

D. \(n = 6\).

Câu 2: Số \(9\) là căn bậc hai số học của số

A. \( - 81\).

B. 81.

C. \(3\).

D. \( - 3\).

Câu 3: Làm tròn số 35,3256 với độ chính xác 0,05 là

A. 35,3.

B. 35,33.

C. 35,32.

D. 35,325.

Câu 4: Các giá trị của \(x\) thoả mãn \(\left| x \right| - 1 = 3\) là

A. \(x = 4\).

B. \(x = 4,x =  - 4\).

C. \(x = 2,x =  - 2\).

D. \(x =  - 4\).

Câu 5: Tam giác ABC có \(\widehat A = 65^\circ ;\widehat B = 55^\circ \). Khẳng định đúng là:

A. AB > AC > BC.

B. BC > AC > AB.

C. AC > BC > AB.

D. BC > AB > AC.

Câu 6: Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để \(\Delta ABC = \Delta ADE(g - c - g)\).

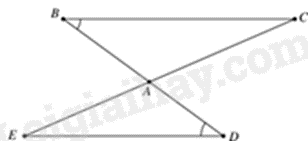
A. \(AB = AD\).

B. \(\widehat {BCA} = \widehat {AED}\).

C. \(\widehat {BCA} = \widehat {DEA}\).

D. \(AC = AE\).

Câu 7: Giá trị của \(x\) trong đẳng thức \(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\) là

A. 75.

B. \( - 3\).

C. \(3\).

D. \( - 75\).

Câu 8: Cho đa thức \(f\left( x \right) = {x^2} + 2x - 3\). Các nghiệm của đa thức đã cho là:

A. 1.

B. 1 và -3.

C. -3.

D. 2 và -3.

Câu 9: Bảng dữ liệu sau cho biết “Số bạn tham gia các hoạt động trong một giờ ra chơi” của học sinh lớp 7A.

Số học sinh tham gia hoạt động Đá cầu và Nhảy dây trong giờ ra chơi là

A. 12.

B. 14.

C. 26.

D. 40.

Câu 10: Bạn Tuấn gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 5 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 5 chấm là

A. \(\frac{7}{{10}}\).

B. \(\frac{5}{{10}}\).

C. \(\frac{4}{{10}}\).

D. \(\frac{3}{{10}}\).

Câu 11: Cho \(\Delta ABC\) có M là trung điểm của BC. Gọi G là trọng tâm của \(\Delta ABC\) và \(AG = 12cm\). Độ dài đoạn thẳng AM là:

A. 18cm.

B. 12cm.

C. 14cm.

D. 13cm.

Câu 12: Một khối Rubik 3 x 3 là một hình lập phương có cạnh dài 5,6 cm. Thể tích của khối Rubik (làm tròn kết quả đến hàng phần chục) là

A. \(175,62c{m^3}\).

B. \(175,7c{m^3}\).

C. \(175,6c{m^2}\).

D. \(175,6c{m^3}\).

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

a) Tính giá trị của biểu thức sau: \({\left( { - 2} \right)^3} + 1\frac{1}{3}.\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\).

b) Tìm \(x\), biết: \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\).

c) Tìm hai số \(x\) và \(y\) biết \(\frac{x}{3} = \frac{y}{2}\) và \(2x + y = 40\).

Bài 2. (1,5 điểm) Cho hai đa thức \(A\left( x \right) = {x^3} - 3{x^2} + 2x - \frac{1}{2}\) và \(B\left( x \right) =  - {x^3} + 7{x^2} - 6x + \frac{3}{2}\).

a) Tìm bậc của đa thức \(A\left( x \right)\) và tính giá trị của \(A\left( x \right)\) tại \(x = 1\).

b) Tính \(Q\left( x \right) = A\left( x \right) + B\left( x \right)\).

c) Tìm đa thức \(P\left( x \right) = \left( {x - 1} \right)Q\left( x \right)\).

Bài 3. (1 điểm) Trong một buổi lao động trồng cây, ba bạn Bình, An và Toàn trồng được số cây tỉ lệ với các số 5; 3; 4. Tính số cây mỗi bạn trồng được, biết tổng số cây trồng được của ba bạn là 48 cây.

Bài 4. (1 điểm) Gạch đặc nung là loại gạch được làm bằng đất sét và được nung nguyên khối, không có lỗ rỗng. Do kết cấu khối đặc nên gạch khá cứng chắc, ít thấm nước, đảm bảo kết cấu các công trình. Một viên gạch (hình vẽ bên) là một hình hộp chữ nhật có kích thước dài 20 cm, rộng 9 cm, cao 5,5 cm.

a) Tính thể tích viên gạch và số mét khối đất sét cần dùng để làm 5000 viên gạch có kích thước như trên.

b) Tính số tiền bác Nam dùng để mua 5000 viên gạch trên, biết giá tiền một viên gạch là 1100 đồng và bác Nam được giảm 5% tổng số tiền phải thanh toán.

Bài 5. (2 điểm) Cho tam giác ABC cân tại A. Kẻ đường cao AH của \(\Delta ABC\) \(\left( {H \in BC} \right)\). Gọi N là trung điểm của AC. Hai đoạn thẳng BN và AH cắt nhau tại G. Trên tia đối của tia NG lấy điểm K sao cho GK = GB. Gọi I là giao điểm của KH và CG.

a) Chứng minh \(\Delta ABH = \Delta ACH\).

b) Chứng minh \(CK \bot BC\).

c) Gọi M là trung điểm AB. Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Số nguyên \(n\) thỏa mãn đẳng thức \({\left( {\frac{8}{{27}}} \right)^n} = {\left( {\frac{2}{3}} \right)^{12}}\) là

A. \(n = 12\).

B. \(n = 8\).

C. \(n = 4\).

D. \(n = 6\).

Phương pháp

Đưa \({\left( {\frac{2}{3}} \right)^{12}}\) về cơ số \(\frac{8}{{27}}\).

Lời giải

Ta có: \({\left( {\frac{2}{3}} \right)^{12}} = {\left( {\frac{2}{3}} \right)^{3.4}} = {\left[ {{{\left( {\frac{2}{3}} \right)}^3}} \right]^4} = {\left( {\frac{8}{{27}}} \right)^4}\) nên \(n = 4\).

Đáp án: C.

Câu 2: Số \(9\) là căn bậc hai số học của số

A. \( - 81\).

B. 81.

C. \(3\).

D. \( - 3\).

Phương pháp

a là căn bậc hai số học của \({a^2}\).

Lời giải

Số 9 là căn bậc hai số học của \({9^2} = 81\).

Đáp án: B.

Câu 3: Làm tròn số 35,3256 với độ chính xác 0,05 là

A. 35,3.

B. 35,33.

C. 35,32.

D. 35,325.

Phương pháp

Làm tròn số thập phân dương:

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    +Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên.

Lời giải

Làm tròn với độ chính xác 0,05 là làm tròn đến hàng phần mười.

Chữ số cần làm tròn là 3.

Sau chữ số 3 là số 2 < 5 nên ta giữ nguyên chữ số 3.

Vậy 35,3256 làm tròn với độ chính xác 0,05 là 35,3.

Đáp án: A.

Câu 4: Các giá trị của \(x\) thoả mãn \(\left| x \right| - 1 = 3\) là

A. \(x = 4\).

B. \(x = 4,x =  - 4\).

C. \(x = 2,x =  - 2\).

D. \(x =  - 4\).

Phương pháp

Chuyển vế.

\(\left| x \right| = a\) thì \(x = a\) hoặc \(x =  - a\).

Lời giải

Ta có:

\(\begin{array}{l}\left| x \right| - 1 = 3\\\left| x \right| = 3 + 1\\\left| x \right| = 4\end{array}\)

Suy ra \(x = 4\) hoặc \(x =  - 4\).

Đáp án: B.

Câu 5: Tam giác ABC có \(\widehat A = 65^\circ ;\widehat B = 55^\circ \). Khẳng định đúng là:

A. AB > AC > BC.

B. BC > AC > AB.

C. AC > BC > AB.

D. BC > AB > AC.

Phương pháp

Áp dụng định lí tổng ba góc trong tam giác bằng \(180^\circ \) để tính \(\widehat C\).

So sánh cạnh dựa vào góc đối diện.

Góc nào lớn hơn thì cạnh đối diện lớn hơn.

Lời giải

Áp dụng định lí tổng ba góc vào tam giác ABC, ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \)

Suy ra \(\widehat C = 180^\circ  - \widehat A - \widehat B\)

\(\widehat C = 180^\circ  - 65^\circ  - 55^\circ  = 60^\circ \).

Vì \(\widehat A > \widehat C > \widehat B\) (\(65^\circ  > 60^\circ  > 55^\circ \)) nên \(BC > AB > AC\).

Đáp án: D.

Câu 6: Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để \(\Delta ABC = \Delta ADE(g - c - g)\).

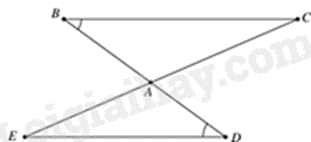
A. \(AB = AD\).

B. \(\widehat {BCA} = \widehat {AED}\).

C. \(\widehat {BCA} = \widehat {DEA}\).

D. \(AC = AE\).

Phương pháp

Xác định các yếu tố đã có trong hình.

Bổ sung yếu tố còn thiếu.

Lời giải

Theo hình vẽ, \(\Delta ABC\) và \(\Delta ADE\) có:

\(\widehat {ABC} = \widehat {ADE}\) (gt)

\(\widehat {BAC} = \widehat {DAE}\) (hai góc đối đỉnh)

Để \(\Delta ABC = \Delta ADE(g - c - g)\) thì cạnh xen giữa \(AB = AD\).

Vậy cần thêm \(AB = AD\) thì \(\Delta ABC = \Delta ADE(g - c - g)\).

Đáp án: A.

Câu 7: Giá trị của \(x\) trong đẳng thức \(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\) là

A. 75.

B. \( - 3\).

C. \(3\).

D. \( - 75\).

Phương pháp

Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) thì \(c = \frac{{ad}}{b}\).

Lời giải

Với \(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\) thì \(x = \frac{{\left( { - 1} \right).\left( { - 15} \right)}}{5} = 3\).

Đáp án: C.

Câu 8: Cho đa thức \(f\left( x \right) = {x^2} + 2x - 3\). Các nghiệm của đa thức đã cho là:

A. 1.

B. 1 và -3.

C. -3.

D. 2 và -3.

Phương pháp

Thay các số trong đáp án vào đa thức để kiểm tra.

Lời giải

Ta có:

\(f\left( 1 \right) = {1^2} + 2.1 - 3 = 0\) nên 1 là nghiệm của đa thức.

\(f\left( { - 3} \right) = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\) nên -3 là nghiệm của đa thức.

\(f\left( 2 \right) = {2^2} + 2.2 - 3 = 5\) nên 2 không là nghiệm của đa thức.

Vậy 1 và -3 là các nghiệm của đa thức đã cho.

Đáp án: B.

Câu 9: Bảng dữ liệu sau cho biết “Số bạn tham gia các hoạt động trong một giờ ra chơi” của học sinh lớp 7A.

Số học sinh tham gia hoạt động Đá cầu và Nhảy dây trong giờ ra chơi là

A. 12.

B. 14.

C. 26.

D. 40.

Phương pháp

Số học sinh tham gia Đá cầu và Nhảy dây bằng tổng số học sinh tham gia hai hoạt động đó.

Lời giải

Số học sinh tham gia hoạt động Đá cầu và Nhảy dây trong giờ ra chơi là:

12 + 14 = 26 (bạn)

Đáp án: C.

Câu 10: Bạn Tuấn gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 5 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 5 chấm là

A. \(\frac{7}{{10}}\).

B. \(\frac{5}{{10}}\).

C. \(\frac{4}{{10}}\).

D. \(\frac{3}{{10}}\).

Phương pháp

Xác suất xuất hiện = số lần xuất hiện : tổng số lần gieo.

Lời giải

Xác suất xuất hiện mặt 5 chấm là: \(\frac{3}{{10}}\).

Đáp án: D.

Câu 11: Cho \(\Delta ABC\) có M là trung điểm của BC. Gọi G là trọng tâm của \(\Delta ABC\) và \(AG = 12cm\). Độ dài đoạn thẳng AM là:

A. 18cm.

B. 12cm.

C. 14cm.

D. 13cm.

Phương pháp

Sử dụng tính chất của trọng tâm: Khoảng cách từ đỉnh đến trọng tâm bằng \(\frac{2}{3}\) độ dài trung tuyến từ đỉnh ấy.

Lời giải

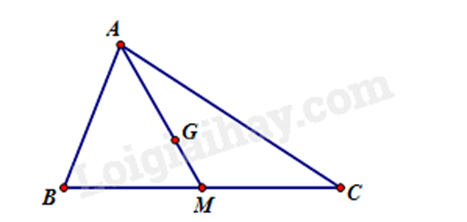
Vì M là trung điểm của \(\Delta ABC\) nên AM là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm nên \(AG = \frac{2}{3}AM\), suy ra \(AM = \frac{3}{2}AG = \frac{3}{2}.12 = 18\left( {cm} \right)\).

Đáp án: A.

Câu 12: Một khối Rubik 3 x 3 là một hình lập phương có cạnh dài 5,6 cm. Thể tích của khối Rubik (làm tròn kết quả đến hàng phần chục) là

A. \(175,62c{m^3}\).

B. \(175,7c{m^3}\).

C. \(175,6c{m^2}\).

D. \(175,6c{m^3}\).

Phương pháp

Thể tích của hình lập phương: \(V = {a^3}\) với a là độ dài cạnh.

Lời giải

Thể tích của khối Rubik là:

\(5,{6^3} = 175,616 \approx 175,6\left( {c{m^3}} \right)\)

Đáp án: D.

Phần tự luận.

Bài 1. (1,5 điểm)

a) Tính giá trị của biểu thức sau: \({\left( { - 2} \right)^3} + 1\frac{1}{3}.\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\).

b) Tìm \(x\), biết: \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\).

c) Tìm hai số \(x\) và \(y\) biết \(\frac{x}{3} = \frac{y}{2}\) và \(2x + y = 40\).

Phương pháp

a) Sử dụng kết hợp kiến thức về luỹ thừa, giá trị tuyệt đối và căn bậc hai số học để tính giá trị.

b) Chuyển vế.

\(\left| x \right| = a\) thì \(x = a\) hoặc \(x =  - a\).

c) Sử dụng tính chất của dãy tỉ số bằng nhau để tìm \(x,y\).

Lời giải

a) \({\left( { - 2} \right)^3} + 1\frac{1}{3}.\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\)

\( =  - 8 + \frac{4}{3}.2,5 - 7:\frac{7}{5}\)

\( =  - 8 + \frac{4}{3}.\frac{5}{2} - 7.\frac{5}{7}\)

\( =  - 8 + \frac{{10}}{3} - 5\)

\( =  - 8 - 5 + \frac{{10}}{3}\)

\( =  - 13 + \frac{{10}}{3}\)

\( = \frac{{ - 29}}{3}\)

b) \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\)

\(\left| {2x - 1} \right| = \frac{1}{2} + \frac{1}{3}\)

\(\left| {2x - 1} \right| = \frac{5}{6}\)

Suy ra \(2x - 1 = \frac{5}{6}\) hoặc \(2x - 1 = \frac{{ - 5}}{6}\)

Trường hợp 1:

\(\begin{array}{l}2x - 1 = \frac{5}{6}\\2x = \frac{5}{6} + 1\\2x = \frac{{11}}{6}\\x = \frac{{11}}{6}:2\\x = \frac{{11}}{{12}}\end{array}\)

Trường hợp 2:

\(\begin{array}{l}2x - 1 = \frac{{ - 5}}{6}\\2x = \frac{{ - 5}}{6} + 1\\2x = \frac{1}{6}\\x = \frac{1}{6}:2\\x = \frac{1}{{12}}\end{array}\)

Vậy \(x = \frac{{11}}{{12}}\); \(x = \frac{1}{{12}}\).

c) Vì \(\frac{x}{3} = \frac{y}{2}\) nên \(\frac{{2x}}{6} = \frac{y}{2}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{{2x}}{6} = \frac{y}{2} = \frac{{2x + y}}{{6 + 2}} = \frac{{40}}{8} = 5\)

Vì \(\frac{{2x}}{6} = 5\) nên \(2x = 5.6\) suy ra \(x = \frac{{5.6}}{2} = 15\)

Vì \(\frac{y}{2} = 5\) nên \(y = 5.2 = 10\)

Vậy \(x = 15\);\(y = 10\).

Bài 2. (1,5 điểm) Cho hai đa thức \(A\left( x \right) = {x^3} - 3{x^2} + 2x - \frac{1}{2}\) và \(B\left( x \right) =  - {x^3} + 7{x^2} - 6x + \frac{3}{2}\).

a) Tìm bậc của đa thức \(A\left( x \right)\) và tính giá trị của \(A\left( x \right)\) tại \(x = 1\).

b) Tính \(Q\left( x \right) = A\left( x \right) + B\left( x \right)\).

c) Tìm đa thức \(P\left( x \right) = \left( {x - 1} \right)Q\left( x \right)\).

Phương pháp

a) Bậc của đa thức là bậc của hạng tử có số mũ lớn nhất.

Thay \(x = 1\) vào \(A\left( x \right)\) để tính giá trị.

b) Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc (theo hàng ngang).

c) Muốn nhân một đa thức với một đa thức, ta làm như sau:

- Nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia.

- Cộng các tích với nhau.

Lời giải

a) \(A\left( x \right) = {x^3} - 3{x^2} + 2x - \frac{1}{2}\)

- Bậc của đa thức \(A\left( x \right)\) là 3 vì hạng tử có số mũ lớn nhất là 3.

- Tại \(x = 1\), ta có:

\(\begin{array}{l}A\left( 1 \right) = {1^3} - {3.1^2} + 2.1 - \frac{1}{2}\\ = 1 - 3 + 2 - \frac{1}{2}\\ =  - \frac{1}{2}\end{array}\)

Vậy \(A\left( 1 \right) =  - \frac{1}{2}\).

b) Ta có:

\(\begin{array}{l}Q\left( x \right) = A\left( x \right) + B\left( x \right)\\ = \left( {{x^3} - 3{x^2} + 2x - \frac{1}{2}} \right) + \left( { - {x^3} + 7{x^2} - 6x + \frac{3}{2}} \right)\\ = {x^3} - 3{x^2} + 2x - \frac{1}{2} - {x^3} + 7{x^2} - 6x + \frac{3}{2}\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 3{x^2} + 7{x^2}} \right) + \left( {2x - 6x} \right) + \left( { - \frac{1}{2} + \frac{3}{2}} \right)\\ = 4{x^2} - 4x + 1\end{array}\)

Vậy \(Q\left( x \right) = 4{x^2} - 4x + 1\).

c) Ta có:

\(\begin{array}{l}P\left( x \right) = \left( {x - 1} \right)Q\left( x \right)\\ = \left( {x - 1} \right)\left( {4{x^2} - 4x + 1} \right)\\ = 4{x^3} - 4{x^2} + x - 4{x^2} + 4x - 1\\ = 4{x^3} + \left( { - 4{x^2} - 4{x^2}} \right) + \left( {x + 4x} \right) - 1\\ = 4{x^3} - 8{x^2} + 5x - 1\end{array}\)

Vậy \(Q\left( x \right) = 4{x^3} - 8{x^2} + 5x - 1\).

Bài 3. (1 điểm) Trong một buổi lao động trồng cây, ba bạn Bình, An và Toàn trồng được số cây tỉ lệ với các số 5; 3; 4. Tính số cây mỗi bạn trồng được, biết tổng số cây trồng được của ba bạn là 48 cây.

Phương pháp

Gọi số cây mà ba bạn Bình, An và Toàn trồng được lần lượt là \(x,y,z\) \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)

Theo đề bài ra ta có: \(\frac{x}{5} = \frac{y}{3} = \frac{z}{4}\) và \(x + y + z = 48\)

Áp dụng tính chất dãy tỉ số bằng nhau để tìm \(x,y,z\).

Lời giải

Gọi số cây mà ba bạn Bình, An và Toàn trồng được lần lượt là \(x,y,z\) \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)

Theo đề bài ra ta có: \(\frac{x}{5} = \frac{y}{3} = \frac{z}{4}\) và \(x + y + z = 48\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{5} = \frac{y}{3} = \frac{z}{4} = \frac{{x + y + z}}{{5 + 3 + 4}} = \frac{{48}}{{12}} = 4\)

\(\frac{x}{5} = 4\) suy ra \(x = 20\)

\(\frac{y}{3} = 4\) suy ra \(y = 12\)

\(\frac{z}{4} = 4\) suy ra \(z = 16\)

Các giá trị \(x = 12;y = 16;z = 20\) thỏa mãn điều kiện.

Vậy số cây ba bạn Bình, An và Toàn trồng được lần lượt là 20, 12, 16 cây.

Bài 4. (1 điểm) Gạch đặc nung là loại gạch được làm bằng đất sét và được nung nguyên khối, không có lỗ rỗng. Do kết cấu khối đặc nên gạch khá cứng chắc, ít thấm nước, đảm bảo kết cấu các công trình. Một viên gạch (hình vẽ bên) là một hình hộp chữ nhật có kích thước dài 20 cm, rộng 9 cm, cao 5,5 cm.

a) Tính thể tích viên gạch và số mét khối đất sét cần dùng để làm 5000 viên gạch có kích thước như trên.

b) Tính số tiền bác Nam dùng để mua 5000 viên gạch trên, biết giá tiền một viên gạch là 1100 đồng và bác Nam được giảm 5% tổng số tiền phải thanh toán.

Phương pháp

a) Thể tích hình hộp chữ nhật = chiều dài . chiều rộng . chiều cao

Thể tích đất sét làm 5000 viên gạch = 5000 . thể tích một viên gạch

Đổi đơn vị về mét khối: \(1c{m^3} = \frac{1}{{1000000}}{m^3}\).

b) Tính số tiền = số viên gạch . giá viên gạch . (100% - 5%).

Lời giải

a) Thể tích một viên gạch là: \(20.9.5,5 = 990\left( {c{m^3}} \right)\).

Thể tích đất sét cần dùng để làm 5000 viên gạch có kích thước như trên là:

\(5000.990 = 4950000\left( {c{m^3}} \right) = 4,95\left( {{m^3}} \right)\).

b) Số tiền bác Nam dùng để mua số gạch trên là:

\(5000.1100.\left( {100\%  - 5\% } \right) = 5225000\) (đồng).

Bài 5. (2 điểm) Cho tam giác ABC cân tại A. Kẻ đường cao AH của \(\Delta ABC\) \(\left( {H \in BC} \right)\). Gọi N là trung điểm của AC. Hai đoạn thẳng BN và AH cắt nhau tại G. Trên tia đối của tia NG lấy điểm K sao cho GK = GB. Gọi I là giao điểm của KH và CG.

a) Chứng minh \(\Delta ABH = \Delta ACH\).

b) Chứng minh \(CK \bot BC\).

c) Gọi M là trung điểm AB. Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\).

Phương pháp

a) Chứng minh \(\Delta ABH = \Delta ACH\)

Chứng minh \(\Delta AHB = \Delta AHC\) theo trường hợp cạnh huyền – cạnh góc vuông.

b) Chứng minh \(CK \bot BC\)

Chứng minh \(G\) là trọng tâm của \(\Delta ABC\) nên \(GN = \frac{1}{2}GK\)

suy ra \(N\) là trung điểm của \(GK\)

Chứng minh \(\Delta ANG = \Delta CNK\) (c.g.c) suy ra \(\widehat {GAN} = \widehat {KCN}\) (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên \(AH\parallel KC\)

Kết hợp với \(AH \bot BC\) nên \(KC \bot BC\).

c) Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\)

Chứng minh \(G\) là trọng tâm của \(\Delta ABC\) nên \(GC = 2GM\) và \(GH = \frac{1}{2}GA\).

Áp dụng bất đẳng thức tam giác vào \(\Delta GHC\) ta có: \(GC < GH + HC\)

Biến đổi để xuất hiện \(GM < \frac{1}{4}\left( {BC + AG} \right)\).

Lời giải

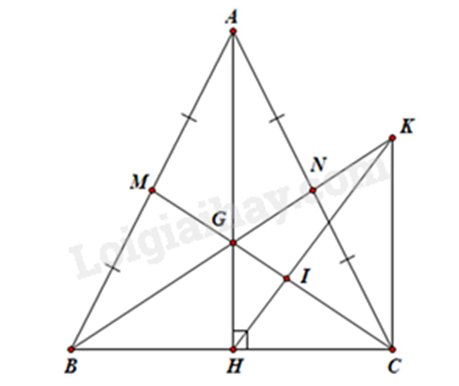
a) Chứng minh \(\Delta ABH = \Delta ACH\)

Vì \(AH\) là đường cao của \(\Delta ABC\) (gt) nên \(AH \bot BC\)

Suy ra \(\Delta AHB\) vuông tại \(H\) và \(\Delta AHC\) vuông tại \(H\)

Xét \(\Delta AHB\) vuông và \(\Delta AHC\) vuông có:

\(AB = AC\) (do \(\Delta ABC\) cân tại \(A\))

\(AH\) là cạnh chung

Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông).

b) Chứng minh \(CK \bot BC\)

Xét \(\Delta ABC\) có hai đường trung tuyến \(AH\) và \(BN\) cắt nhau tại \(G\) nên \(G\) là trọng tâm của \(\Delta ABC\)

Suy ra \(GN = \frac{1}{2}GB\) mà \(GB = GK\) nên \(GN = \frac{1}{2}GK\)

Do đó \(N\) là trung điểm của \(GK\)

Xét \(\Delta ANG\) và \(\Delta CNK\) có:

\(AN = NC\) (do \(N\) là trung điểm của \(AC\))

\(\widehat {ANG} = \widehat {CNK}\) (hai góc đối đỉnh)

\(NG = NK\) (do \(N\) là trung điểm của \(GK\))

Do đó \(\Delta ANG = \Delta CNK\) (c.g.c)

Suy ra \(\widehat {GAN} = \widehat {KCN}\) (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên \(AH\parallel KC\)

Lại có \(AH \bot BC\) nên \(KC \bot BC\).

c) Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\)

Vì \(G\) là trọng tâm của \(\Delta ABC\), mà \(CM\) là đường trung tuyến của \(\Delta ABC\) nên \(G \in CM\).

Vì \(G\) là trọng tâm của \(\Delta ABC\) nên \(GC = 2GM\) và \(GH = \frac{1}{2}GA\).

Xét \(\Delta GHC\) có: \(GC < GH + HC\)

suy ra \(2GM < \frac{1}{2}GA + \frac{1}{2}BC = \frac{1}{2}\left( {BC + AG} \right)\)

Do đó \(GM < \frac{1}{4}\left( {BC + AG} \right)\).