Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8

Lý thuyết

* Sự đồng quy của ba đường trung tuyến trong một tam giác

- Đường trung tuyến của tam giác

Đoạn thẳng \(AM\) nối đỉnh \(A\) của tam giác \(ABC\) với trung điểm \(M\) của cạnh \(BC\) gọi là đường trung tuyến (xuất phát từ đỉnh \(A\) hoặc ứng với cạnh \(BC\)) của tam giác \(ABC\).

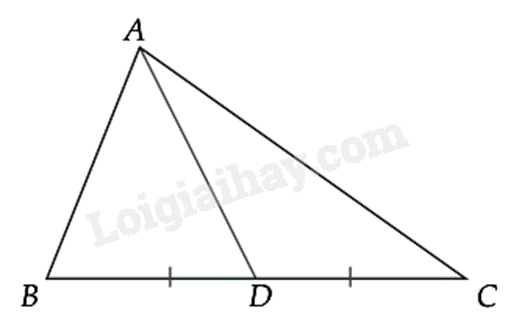
- Định lí: Ba đường trung tuyến của tam giác cùng đi qua một điểm (hay đồng qui tại một điểm). Điểm đó cách mỗi đỉnh một khoảng bằng \(\frac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.

Gọi \(G\) là trọng tâm của tam giác \(ABC\). Khi đó:

\(\frac{{AG}}{{AM}} = \frac{{BG}}{{BN}} = \frac{{CG}}{{CD}} = \frac{2}{3}\)

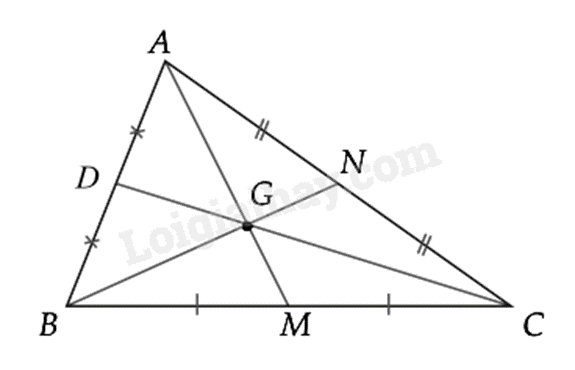
* Sự đồng quy của ba đường phân giác trong một tam giác

- Đường phân giác của tam giác

Trong tam giác \(ABC\) tia phân giác của góc \(A\) cắt cạnh \(BC\) tại điểm \(D\) thì đoạn thẳng \(AD\) được gọi là đường phân giác (xuất phát từ đỉnh \(A\)) của tam giác \(ABC\).

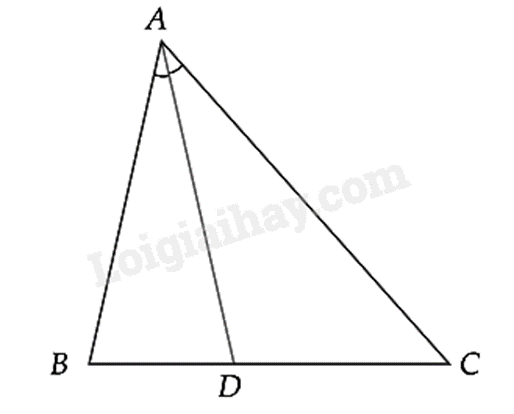
- Định lí: Ba đường phân giác của một tam giác đồng qui tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.

Gọi \(O\) là giao điểm của ba đường phân giác \(AD\), \(BE\) và \(CF\). Ta có \(OH = OI = OK\).

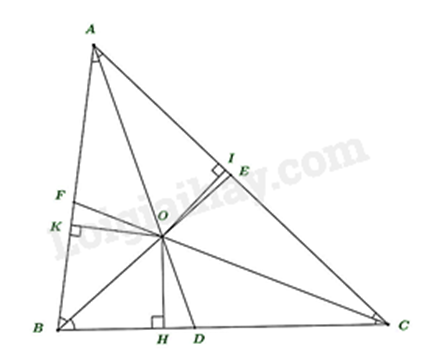
* Sự đồng quy của ba đường trung trực

- Đường trung trực của tam giác

Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó

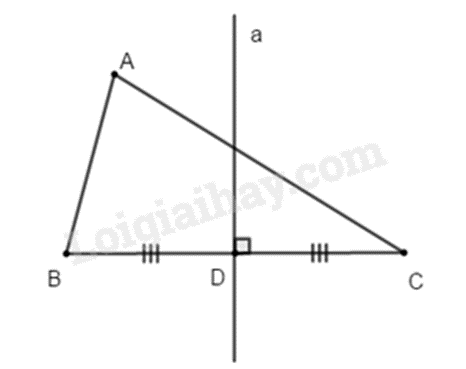
Mỗi tam giác có ba đường trung trực.

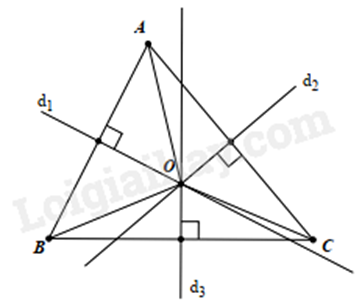
- Định lí: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

Nhận xét: Giao điểm ba đường trung trực O của tam giác \({\rm{\Delta }}ABC\) cách đều ba đỉnh của tam giác \(OA = OB = OC\).

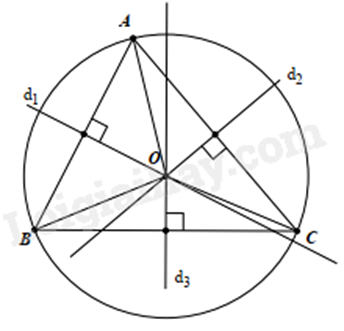
Vậy điểm O là tâm của đường tròn ngoại tiếp \(\Delta ABC\).

* Sự đồng quy của ba đường cao

- Đường cao trong tam giác

Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đưởng thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

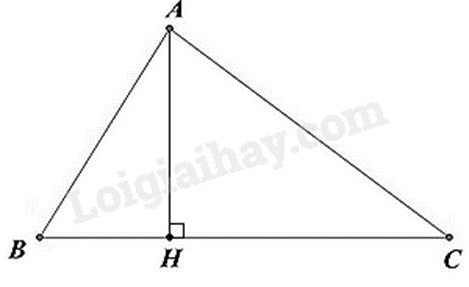
- Định lí: Ba đường cao của tam giác đồng quy tại một điểm.

Chú ý

a) Điểm đồng quy ba đường cao của tam giác là trực tâm của tam giác

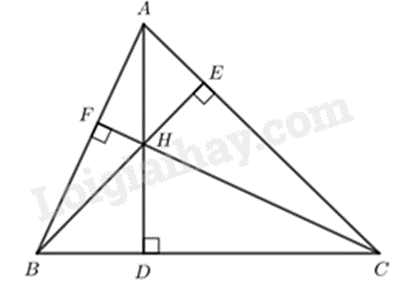
b) Gọi \(H\) là trực tâm \(\Delta ABC\) (hình vẽ) ta có:

- Khi \(\Delta ABC\) nhọn thì \(H\) nằm bên trong tam giác.

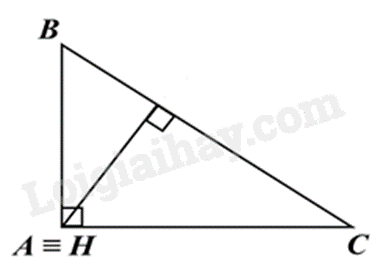
- Khi \(\Delta ABC\) vuông tại A thì \(H\) trùng với \(A\).

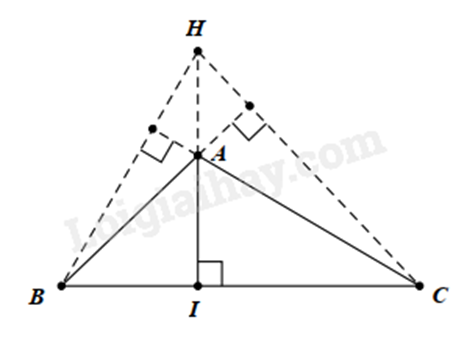
- Khi \(\Delta ABC\) tù thì \(H\) nằm bên ngoài tam giác.

* Lưu ý:

- Trong tam giác cân, đường phân giác ở đỉnh đồng thời là đường trung tuyến, đường cao, đường trung trực.

 - Nếu tam giác có một đường trung tuyến đồng thời là đường trung tuyến/đường cao/đường trung trực thì tam giác đó là tam giác cân.

- Trong tam giác đều, các đường phân giác, đường trung tuyền, đường cao, đường trung trực của tam giác đó trùng nhau và cùng đồng quy tại một điểm.

Bài tập

Bài 1: Chọn câu sai.

A. Trong một tam giác có ba đường trung tuyến.

B. Các đường trung tuyến của tam giác cắt nhau tại một điểm.

C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.

D. Một tam giác có ba trọng tâm.

Bài 2: \(\Delta ABC\) có trung tuyến \(AM = 12{\mkern 1mu} cm\) và trọng tâm \(G\). Độ dài đoạn AG là

A. \(4,5{\mkern 1mu} cm\).

B. \(3{\mkern 1mu} cm\).

C. \(6{\mkern 1mu} cm\).

D. \(8{\mkern 1mu} cm\).

Bài 3: Cho \(\Delta ABC\) có hai đường phân giác CD và BE cắt nhau tại I. Khi đó

A. AI là trung tuyến vẽ từ \(A\).

B. AI là đường cao kẻ từ \(A\).

C. AI là trung trực cạnh BC.

D. AI là phân giác của góc \(A\).

Bài 4: Gọi \(O\) là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó \(O\) là:

A. Điểm cách đều ba cạnh của \(\Delta ABC\).

B. Điểm cách đều ba đỉnh của \(\Delta ABC\).

C. Tâm đường tròn ngoại tiếp \(\Delta ABC\).

D. Đáp án B và C đúng.

Bài 5: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A. Tam giác vuông.

B. Tam giác cân.

C. Tam giác đều.

D. Tam giác vuông cân.

Bài 6: Cho \(\Delta ABC\) cân tại A, có \(\hat A = 40^\circ \), đường trung trực của AB cắt BC ở D. Tính \(\widehat {CAD}\).

A. \(30^\circ \).

B. \(45^\circ \).

C. \(60^\circ \).

D. \(40^\circ \).

Bài 7: Cho \(\Delta ABC\) nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho \(BI = AC\). Trên tia đối của tia CE lấy điểm K sao cho \(CK = AB.\)

a) Chứng minh AI = AK.

b) \(\Delta AIK\) là tam giác gì?

Bài 8: Cho \(G\) là trọng tâm của tam giác đều. Chứng minh rằng \(GA = GB = GC\).

Bài 9: Cho \(\Delta ABC\), các đường trung tuyến BD và CE. So sánh \(BD + CE\) và \(\frac{3}{2}BC\).

Bài 10: Cho \(\Delta ABC\), các tia phân giác của góc \(B\) và \(A\) cắt nhau tại điểm O. Qua \(O\) kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho \(BM = 4cm,CN = 5cm.\) Tính MN?

--------Hết--------

Lời giải chi tiết:

Bài 1: Chọn câu sai.

A. Trong một tam giác có ba đường trung tuyến.

B. Các đường trung tuyến của tam giác cắt nhau tại một điểm.

C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.

D. Một tam giác có ba trọng tâm.

Phương pháp

Sử dụng kiến thức về ba đường trung tuyến.

“ Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.”

Lời giải

Một tam giác chỉ có một trọng tâm nên đáp án D sai.

Đáp án: D

Bài 2: \(\Delta ABC\) có trung tuyến \(AM = 12{\mkern 1mu} cm\) và trọng tâm \(G\). Độ dài đoạn AG là

A. \(4,5{\mkern 1mu} cm\).

B. \(3{\mkern 1mu} cm\).

C. \(6{\mkern 1mu} cm\).

D. \(8{\mkern 1mu} cm\).

Phương pháp

Trọng tâm cách đỉnh một khoảng bằng \(\frac{2}{3}\) đường trung tuyến kẻ từ đỉnh đó.

Lời giải

Vì \(G\) là trọng tâm \(\Delta ABC\) và AM là đường trung tuyến nên \(AG = \frac{2}{3}AM\) (tính chất ba đường trung tuyến của tam giác)

Do đó \(AG = \frac{2}{3}.12 = 8{\mkern 1mu} cm.\)

Đáp án: D

Bài 3: Cho \(\Delta ABC\) có hai đường phân giác CD và BE cắt nhau tại I. Khi đó

A. AI là trung tuyến vẽ từ \(A\).

B. AI là đường cao kẻ từ \(A\).

C. AI là trung trực cạnh BC.

D. AI là phân giác của góc \(A\).

Phương pháp

Ba đường phân giác của tam giác cùng đi qua 1 điểm.

Lời giải

Hai đường phân giác CD và BE cắt nhau tại \(I\) mà ba đường phân giác của một tam giác cùng đi qua một điểm nên AI là phân giác của góc \(A\).

Đáp án: D

Bài 4: Gọi \(O\) là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó \(O\) là:

A. Điểm cách đều ba cạnh của \(\Delta ABC\).

B. Điểm cách đều ba đỉnh của \(\Delta ABC\).

C. Tâm đường tròn ngoại tiếp \(\Delta ABC\).

D. Đáp án B và C đúng.

Phương pháp

Tính chất đồng quy của 3 đường trung trực trong một tam giác.

Lời giải

Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.

Đáp án: D

Bài 5: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A. Tam giác vuông.

B. Tam giác cân.

C. Tam giác đều.

D. Tam giác vuông cân.

Phương pháp

Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.

Lời giải

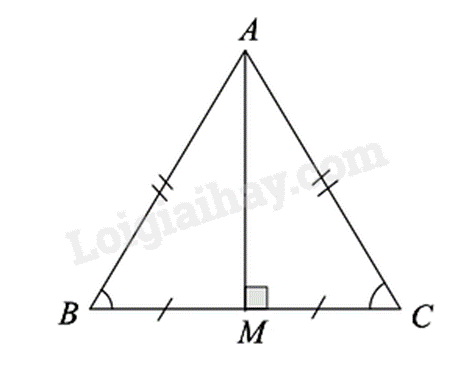
Giả sử \(\Delta ABC\) có AM là trung tuyến đồng thời là đường trung trực.

Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân.

Thật vậy, vì AM là trung tuyến của \(\Delta ABC\) (gt) nên \(BM = MC\) (tính chất trung tuyến)

Vì AM là trung trực của BC nên \(AM \bot BC\)

Xét hai tam giác vuông \(\Delta ABM\) và \(\Delta ACM\) có:

\(BM = CM\left( {cmt} \right)\)

AM chung

Do đó \(\Delta ABM = \Delta ACM\) (2 cạnh góc vuông)

Suy ra \(AB = AC\) (2 cạnh tương ứng) nên \(\Delta ABC\) cân tại A.

Đáp án: B

Bài 6: Cho \(\Delta ABC\) cân tại A, có \(\hat A = 40^\circ \), đường trung trực của AB cắt BC ở D. Tính \(\widehat {CAD}\).

A. \(30^\circ \).

B. \(45^\circ \).

C. \(60^\circ \).

D. \(40^\circ \).

Phương pháp

Áp dụng tính chất đường trung trực của đoạn thẳng, tính chất tam giác cân.

Lời giải

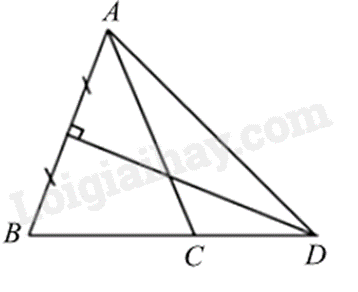
Vì \(\Delta ABC\) cân tại A (gt) suy ra \(\hat B = \hat C = \left( {180^\circ  - \hat A} \right):2 = \left( {180^\circ  - 40^\circ } \right):2 = 70^\circ .\)

Vì \(D\) thuộc đường trung trực của AB nên \(AD = BD\) (tính chất đường trung trực của đoạn thẳng)

suy ra \(\Delta ABD\) cân tại \(D\) (dấu hiệu nhận biết tam giác cân)

Do đó \(\widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \hat B = 70^\circ \)

Suy ra \(\widehat {DAC} = 70^\circ  - \widehat {CAB} = 70^\circ  - 40^\circ  = 30^\circ \)

Đáp án: A

Bài 7: Cho \(\Delta ABC\) nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho \(BI = AC\). Trên tia đối của tia CE lấy điểm K sao cho \(CK = AB.\)

a) Chứng minh AI = AK.

b) \(\Delta AIK\) là tam giác gì?

Phương pháp

Áp dụng tính chất trong tam giác vuông 2 góc nhọn phụ nhau, tính chất 2 góc kề bù, dấu hiệu nhận biết tam giác vuông cân.

Lời giải

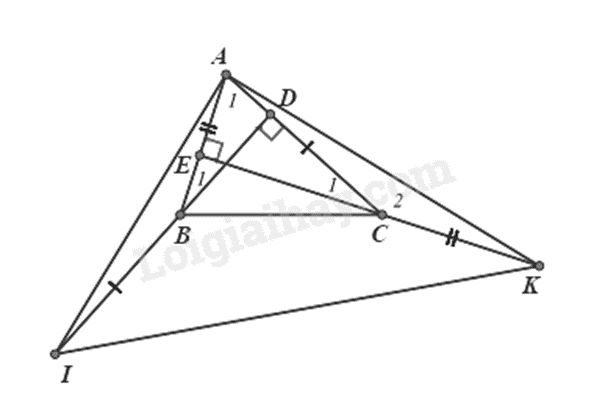
a) Xét \(\Delta ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = 90^\circ \) (trong tam giác vuông 2 góc nhọn phụ nhau)

Xét \(\Delta AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = 90^\circ \) (trong tam giác vuông 2 góc nhọn phụ nhau)

suy ra \(\widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).

Lại có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) và \(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (2) (hai góc kề bù)

Từ \(\left( 1 \right);\;\left( 2 \right)\) suy ra \(\widehat {{B_2}} = \widehat {{C_2}}\).

Xét \(\Delta ABI\) và \(\Delta KCA\) có:

\(AB = CK\left( {gt} \right)\)

\(\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\)

\(BI = AC\left( {gt} \right)\)

do đó \(\Delta ABI = \Delta KCA(c - g - c)\) suy ra \(AI = AK\) (2 cạnh tương ứng)

b) Ta có \(AI = AK\left( {cmt} \right)\) suy ra \(\Delta AIK\) cân tại A (*).

Vì \(\Delta ABI = \Delta KCA\left( {cmt} \right)\) suy ra \(\widehat {AIB} = \widehat {CAK}(3)\) (2 góc tương ứng)

Xét \(\Delta AID\) có: \(\widehat {AID} + \widehat {IAD} = 90^\circ \left( 4 \right)\) (trong tam giác vuông 2 góc nhọn phụ nhau)

Từ (3) và (4) suy ra \(\widehat {IAD} + \widehat {CAK} = 90^\circ \), do đó \(\Delta AIK\) vuông tại A (**)

Từ (*) và (**) suy ra \(\Delta AIK\) vuông cân tại A.

Bài 8: Cho \(G\) là trọng tâm của tam giác đều. Chứng minh rằng \(GA = GB = GC\).

Phương pháp

- Xét các tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.

- Áp dụng tính chất đường trung tuyến của tam giác.

Lời giải

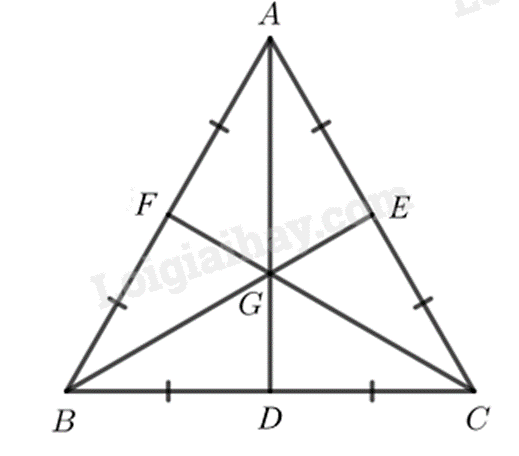
Các tia AG, BG và CG cắt BC, AC, AB lần lượt tại D, E, F thì D, E, F theo thứ tự là trung điểm của BC, AC, AB.

Mà \(BC = AC = AB\) (do \(\Delta ABC\) là tam giác đều), do đó \(BD = DC = CE = EA = AF = FB\)

Xét \(\Delta AEB\) và \(\Delta AFC\) ta có: \(AB = AC;\) \(\hat A\) chung; \(AE = AF.\)

Vậy \(\Delta AEB = \Delta AFC{\mkern 1mu} (c.g.c)\), suy ra \(BE = CF{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)

Chứng minh tương tự ta có \(\Delta BEC = \Delta ADC{\mkern 1mu} (c.g.c)\), suy ra \(BE = AD\left( 2 \right)\)

Từ (1) và (2) ta có: \(AD = BE = CF\left( 3 \right)\)

Theo đề bài \(G\) là trọng tâm của \(\Delta ABC\) nên ta có:

\(GA = \frac{2}{3}AD;{\mkern 1mu} {\mkern 1mu} GB = \frac{2}{3}BE;{\mkern 1mu} {\mkern 1mu} GC = \frac{2}{3}CF\)

Vì thế từ (3) ta suy ra \(GA = GB = GC.\)

Bài 9: Cho \(\Delta ABC\), các đường trung tuyến BD và CE. So sánh \(BD + CE\) và \(\frac{3}{2}BC\).

Phương pháp

+ Sử dụng tính chất đường trung tuyến của tam giác.

+ Sử dụng quan hệ giữa các cạnh trong tam giác.

Lời giải

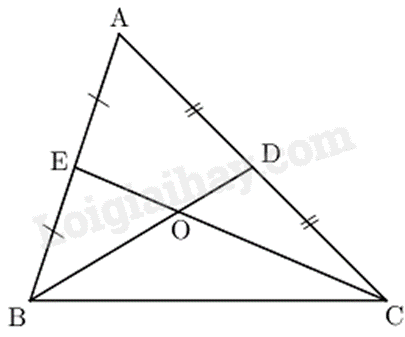
Gọi \(G\) là giao điểm của BD và CE. Trong \(\Delta GBC\) ta có \(BG + CG > BC\)

Ta lại có \(BG = \frac{2}{3}BD;{\mkern 1mu} CG = \frac{2}{3}CE\) (tính chất các đường trung tuyến của \(\Delta ABC\))

Từ đó \(\frac{2}{3}BD + \frac{2}{3}CE > BG + CG\)

suy ra \(\frac{2}{3}\left( {BD + CE} \right) > BC\)

do đó \(BD + CE > \frac{3}{2}BC.\)

Bài 10: Cho \(\Delta ABC\), các tia phân giác của góc \(B\) và \(A\) cắt nhau tại điểm O. Qua \(O\) kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho \(BM = 4cm,CN = 5cm.\) Tính MN?

Phương pháp

Áp dụng tính chất 3 đường phân giác của tam giác, tia phân giác của 1 góc, hai đường thẳng song song và tính chất tam giác cân.

Lời giải

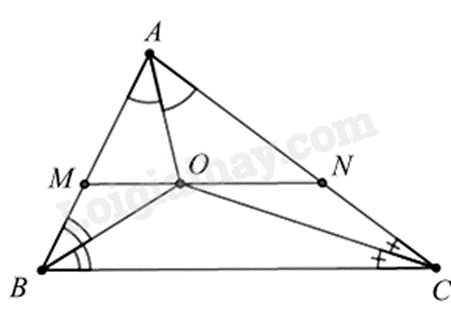
Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\) (gt)

Suy ra CO là phân giác của \(\widehat {ACB}\) (tính chất 3 đường phân giác của tam giác)

Do đó \(\widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)

Vì BO là phân giác của \(\widehat {ABC}\left( {gt} \right)\) nên \(\widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)

Vì MN // BC (gt) nên \(\widehat {MOB} = \widehat {OBC}\left( 3 \right)\) và \(\widehat {NOC} = \widehat {OCB}\left( 4 \right)\) (so le trong)

Từ (1) và (4) suy ra \(\widehat {NOC} = \widehat {NCO}\) suy ra \(\Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)

Vì vậy \(NO = NC = 5cm\) (tính chất tam giác cân)

Từ (2) và (3) suy ra \(\widehat {MOB} = \widehat {MBO}\).

Do đó \(\Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)

suy ra \(MB = MO = 4cm\) (tính chất tam giác cân)

Vậy \(MN = MO + ON = 4 + 5 = 9cm.\)