Dạng bài định lí và chứng minh một định lí - Ôn hè Toán 7 lên 8

Lý thuyết

* Định lí

Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:

Nếu ... thì ...

- Phần giữa từ “nếu” và từ “thì” là giả thiết” của định lí.

- Phần sau của từ “thì” là kết luận của định lí.

* Chứng minh định lí

Chứng minh định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.

Bài tập

Bài 1: Trong các câu sau, câu nào không cho một định lí:

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.

C. Hai góc đối đỉnh thì bằng nhau.

D. Hai góc kề nhau thì có tổng số đo là \(180^\circ \).

Bài 2: Cho định lí: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lí là

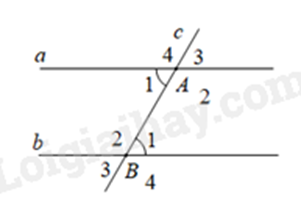
A. a // b; a \( \bot \) c.

B. a // b, c cắt a tại A; c cắt b tại B.

C. a // b; a // c.

D. a // b, c bất kì.

Bài 3: Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lí là:

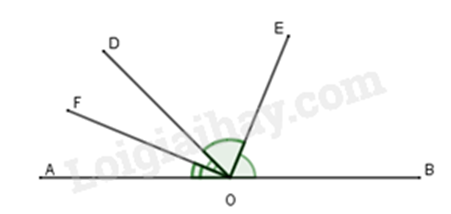
A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.

Kết luận: \(OE \bot OF\).

B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD.

Kết luận: \(OE \bot OA\).

C. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOE.

Kết luận: \(OE \bot OF\).

D. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.

Kết luận: \(OB \bot OF\).

Bài 4: Phần giả thiết:  c cắt a tại A, c cắt b tại B, \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lí nào dưới đây?

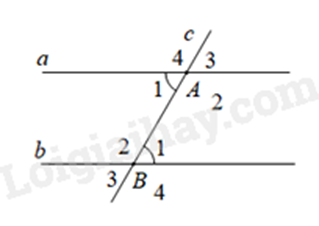
A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song.

B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.

C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Bài 5: Định lí sau được phát biểu thành lời là:

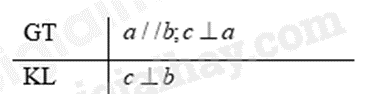
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.

C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ \).

D. Cả A, B, C đều sai.

Bài 6: Vẽ hình và ghi giả thiết, kết luận của các định lí sau:

a) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.

b) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.

Bài 7: Chứng minh định lí "Hai góc đối đỉnh thì bằng nhau".

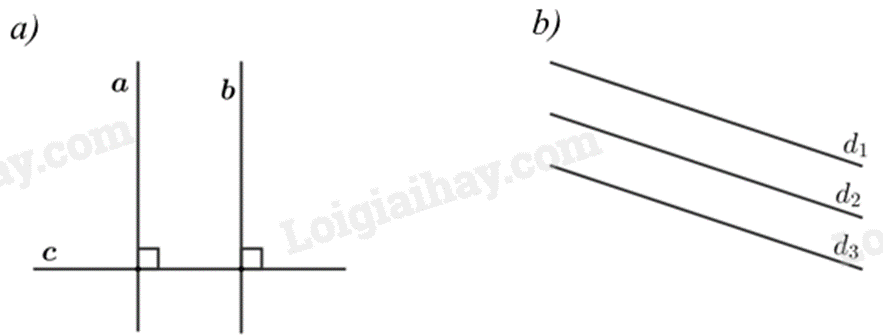
Bài 8: Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau rồi viết giả thiết, kết luận từng định lí.

Bài 9: Chứng minh định lí “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau”.

Bài 10: Vẽ hình, ghi giả thiết kết luận và chứng minh định lí sau “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó cũng cắt đường thẳng còn lại”.

Bài 11: Chứng minh định lí sau: “Tổng ba góc của một tam giác bằng \(180^\circ \)”.

--------Hết--------

Lời giải chi tiết:

Bài 1: Trong các câu sau, câu nào không cho một định lí:

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.

C. Hai góc đối đỉnh thì bằng nhau.

D. Hai góc kề nhau thì có tổng số đo là \(180^\circ \).

Phương pháp

Sử dụng nhận xét về định lí: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.

Lời giải

+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”

+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”

+ “Hai góc đối đỉnh thì bằng nhau”

Câu D không là định lí vì khẳng định D sai

Đáp án: D

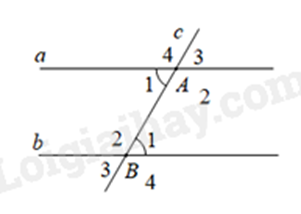
Bài 2: Cho định lí: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lí là

A. a // b; a \( \bot \) c.

B. a // b, c cắt a tại A; c cắt b tại B.

C. a // b; a // c.

D. a // b, c bất kì.

Phương pháp

Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra.

Lời giải

Giả thiết của định lí trên là a // b, c cắt a tại A; c cắt b tại B.

Đáp án: B

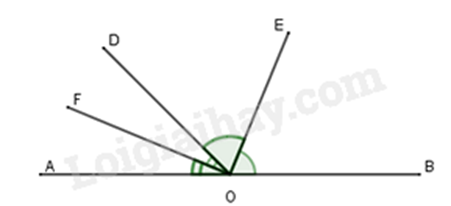
Bài 3: Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lí là:

A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.

Kết luận: \(OE \bot OF\).

B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD.

Kết luận: \(OE \bot OA\).

C. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOE.

Kết luận: \(OE \bot OF\).

D. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.

Kết luận: \(OB \bot OF\).

Phương pháp

Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra

Lời giải

Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.

Kết luận: \(OE \bot OF\).

Đáp án: A

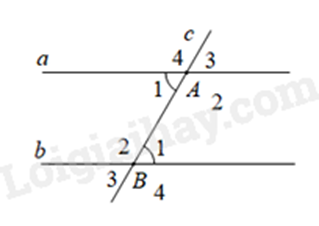
Bài 4: Phần giả thiết:  c cắt a tại A, c cắt b tại B, \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lí nào dưới đây?

A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song.

B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.

C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Phương pháp

Xét vị trí của góc A₁ so với góc B₁ rồi xét giả thiết của từng định lí

Lời giải

Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b

Vậy định lí là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”

Đáp án: B

Bài 5: Định lí sau được phát biểu thành lời là:

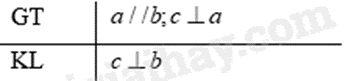
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.

C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ \).

D. Cả A, B, C đều sai.

Phương pháp

Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra.

Lời giải

Định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

Đáp án: A

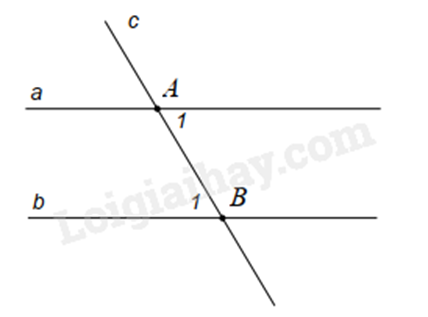
Bài 6: Vẽ hình và ghi giả thiết, kết luận của các định lí sau:

a) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.

b) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.

Phương pháp

Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:

Nếu ... thì ...

- Phần giữa từ “nếu” và từ “thì” là giả thiết” của định lí.

- Phần sau của từ “thì” là kết luận của định lí.

Lời giải

a)

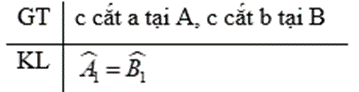
b)

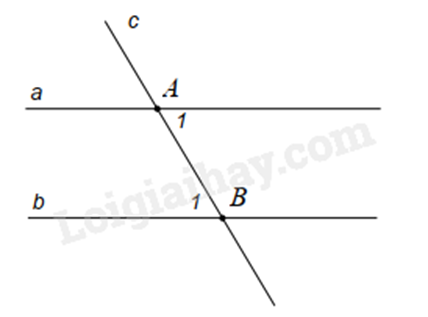
Bài 7: Chứng minh định lí "Hai góc đối đỉnh thì bằng nhau".

Phương pháp

- Vẽ hình, viết giả thiết – kết luận.

- Sử dụng tính chất hai góc kề bù đề chứng minh.

Lời giải

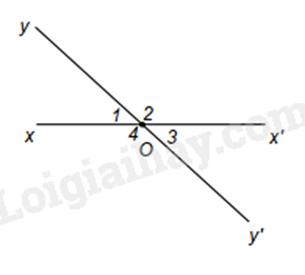
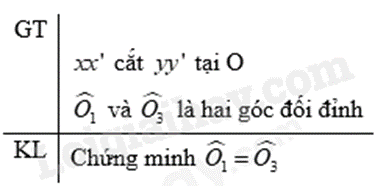
Chứng minh

Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} = 180^\circ \) (hai góc kề bù)

           \(\widehat {{O_3}} + \widehat {{O_2}} = 180^\circ \) (hai góc kề bù)

Suy ra \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {{O_3}} + \widehat {{O_2}}\)

Do đó \(\widehat {{O_1}} = \widehat {{O_3}}\).

Vậy hai góc đối đỉnh bằng nhau.

Bài 8: Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau rồi viết giả thiết, kết luận từng định lí.

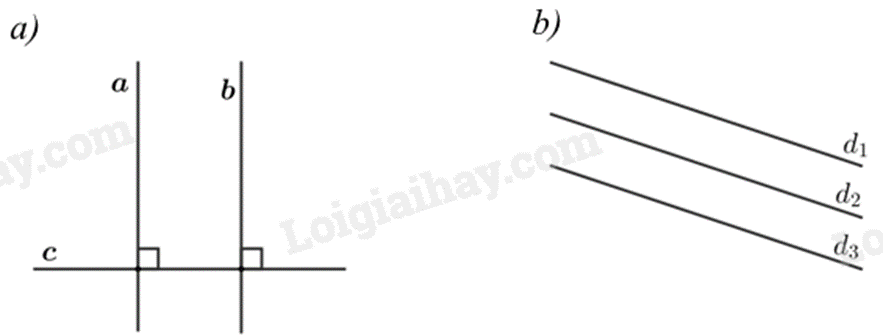
Phương pháp

Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:

Nếu ... thì ...

- Phần giữa từ “nếu” và từ “thì” là giả thiết” của định lí.

- Phần sau của từ “thì” là kết luận của định lí.

Lời giải

a) Định lí: Đường thẳng a và b cùng vuông góc với đường thẳng c thì a // b.

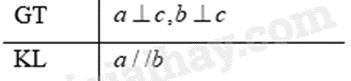
b) Định lí: Đường thẳng \({d_1}\) và \({d_2}\) cùng song song với đường thẳng \({d_3}\) thì \({d_1}\) // \({d_2}\).

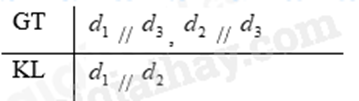
Bài 9: Chứng minh định lí “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau”.

Phương pháp

- Vẽ hình, viết giả thiết – kết luận.

- Sử dụng tính chất hai góc kề bù, tính chất tia phân giác để chứng minh.

- Góc tạo bởi hai đường thẳng vuông góc bằng \(90^\circ \).

Lời giải

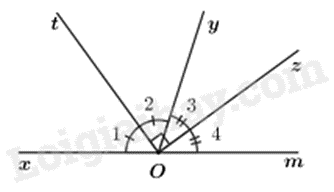
Chứng minh

Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {{O_1}} + \widehat {{O_2}} = \frac{1}{2}\widehat {xOy}\), suy ra \(\widehat {xOy} = 2\widehat {{O_2}}\).

Vì Oz là tia phân giác của \(\widehat {yOm}\) nên \(\widehat {{O_3}} = \widehat {{O_4}} = \frac{1}{2}\widehat {yOm}\), suy ra \(\widehat {yOm} = 2\widehat {{O_3}}\).

Mà \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (hai góc kề bù)

Suy ra \(2\widehat {{O_2}} + 2\widehat {{O_3}} = 180^\circ \)

           \(\begin{array}{l}2\left( {\widehat {{O_2}} + \widehat {{O_3}}} \right) = 180^\circ \\\widehat {{O_2}} + \widehat {{O_3}} = \frac{{180^\circ }}{2}\end{array}\)

Suy ra \(\widehat {tOz} = 90^\circ \) (do \(\widehat {{O_2}}\) và \(\widehat {{O_3}}\) là hai góc kề nhau) hay \(Ot \bot Oz\).

Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau.

Bài 10: Vẽ hình, ghi giả thiết kết luận và chứng minh định lí sau: “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó cũng cắt đường thẳng còn lại”.

Phương pháp

- Vẽ hình, viết giả thiết – kết luận.

- Sử dụng tiên đề Euclid để chứng minh: Qua điểm M chỉ có một đường thẳng duy nhất song song với đường thẳng b, đó là đường thẳng a.

Lời giải

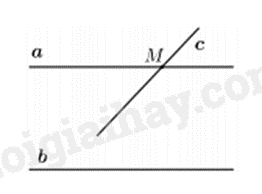
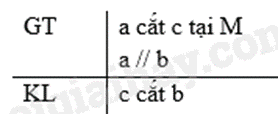
Chứng minh

Giả sử đường thẳng a cắt c tại M.

Theo tiên đề Euclid: Qua điểm M chỉ có một đường thẳng duy nhất song song với đường thẳng b, đó là đường thẳng a.

Do đó đường thẳng c không thể song song với đường thẳng b.

Vậy đường thẳng c cắt đường thẳng b.

Bài 11: Chứng minh định lí sau: “Tổng ba góc của một tam giác bằng \(180^\circ \)”.

Phương pháp

- Vẽ hình, viết giả thiết – kết luận.

- Từ một đỉnh, vẽ đường thẳng song song với cạnh đối diện của nó. Sử dụng tính chất hai đường thẳng song song để chứng minh tổng ba góc của tam giác đó bằng \(180^\circ \).

Lời giải

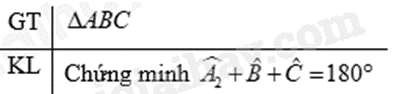
Chứng minh

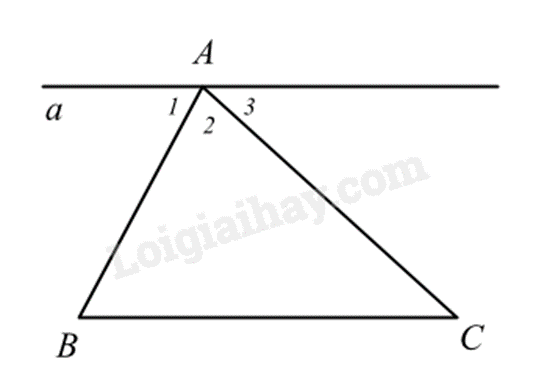
Từ A kẻ đường thẳng a song song với BC.

Vì a // BC nên ta có: \(\widehat B = \widehat {{A_1}},\widehat C = \widehat {{A_2}}\) (hai cặp góc so le trong)

Mà \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{A_3}} = 180^\circ \)

Do đó \(\widehat B + \widehat {{A_2}} + \widehat C = 180^\circ \)

Vậy tổng ba góc của một tam giác bằng \(180^\circ \).