Đề ôn hè Toán 7 lên 8 - Đề 3

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Căn bậc hai số học của số 9 là:

A. 3.

B. -3.

C. 9.

D. -9.

Câu 2: Số nào dưới đây là số thập phân vô hạn tuần hoàn?

A. \(\sqrt {144} \).

B. \(2,\left( 3 \right)\).

C. \( - 1,2345\).

D. \(\pi  = 3,141592653589...\).

Câu 3: Chữ số a thích hợp để \( - 12,6a\left( {456} \right) <  - 12,69321\) là

A. 7.

B. 9.

C. 8.

D. 6.

Câu 4: Cho \(\left| x \right| = 4\) thì giá trị của \(x\) là:

A. \(x = 4\).

B. \(x =  - 2\).

C. \(x = 2\) hoặc \(x =  - 2\).

D. \(x = 4\) hoặc \(x =  - 4\).

Câu 5: Hai góc kề bù là

A. hai góc vừa kề nhau, vừa bù nhau.

B. hai góc có tổng số đo bằng \(90^\circ \).

C. hai góc có tổng số đo bằng \(180^\circ \).

D. hai góc có chung đỉnh.

Câu 6: Tia Ot nào trong các hình dưới đây là tia phân giác của góc \(xOy\)?

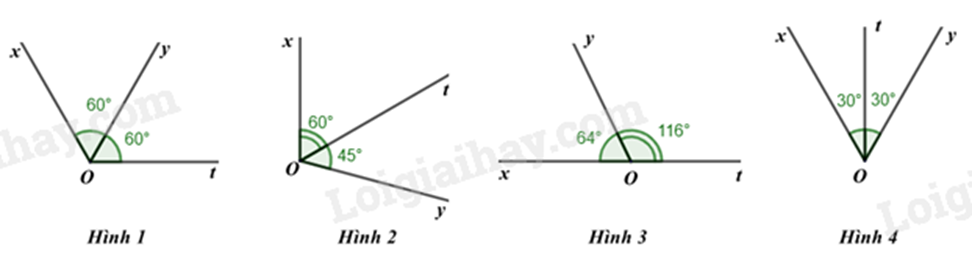
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Câu 7: Dừa sáp là một trong những đặc sản lại, quý hiếm có giá trị dinh dưỡng cao được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng. Nếu mua \(x\left( {x \in \mathbb{N}} \right)\) quả dừa sáp thì người mua phải trả số tiền (đồng) là:

A. \(200000x\).

B. \(200000\).

C. \(200000 + x\).

D. \(\frac{{200000}}{x}\).

Câu 8: Cho đa thức \(B\left( x \right) = 2{x^2} + 5x + 2\). Trong các số sau, số nào là nghiệm của đa thức đã cho.

A. \(x = 2\).

B. \(x = 1\).

C. \(x =  - 1\).

D. \(x =  - 2\).

Câu 9: Cho hình vẽ bên.

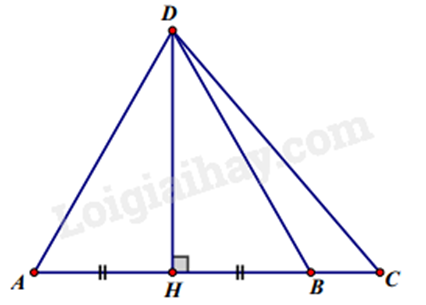
Chọn khẳng định sai trong các khẳng định sau:

A. DA > DH.

B. DC < DH.

C. DA = DB.

D. HB < HC.

Câu 10: Các đường phân giác của tam giác ABC cắt nhau tại D thì

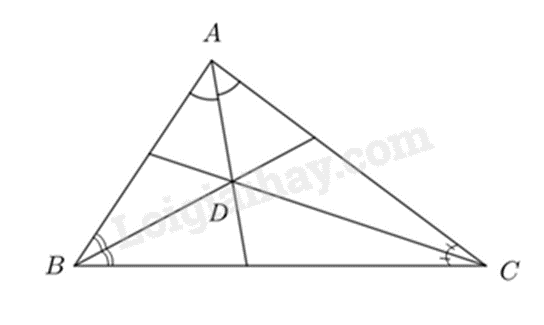
A. điểm D cách đều ba cạnh của tam giác ABC.

B. điểm D là trọng tâm của tam giác ABC.

C. điểm D là trực tâm của tam giác ABC.

D. điểm D cách đều ba đỉnh A, B, C.

Câu 11: Bạn An làm một chiếc hộp đựng quà hình lập phương có cạnh bằng 10 cm. Bỏ qua các mép gấp, diện tích giấy mà bạn An cần dùng là

A. \(60c{m^2}\).

B. \(100c{m^2}\).

C. \(600c{m^2}\).

D. \(1000c{m^2}\).

Câu 12: Một thanh socola hình lăng trụ đứng tam giác có các kích thước như hình vẽ. Thể tích của thanh socola đó là

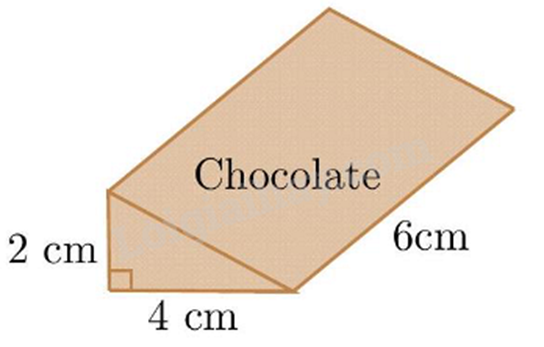
A. \(12c{m^3}\).

B. \(24c{m^3}\).

C. \(36c{m^3}\).

D. \(48c{m^3}\).

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \(\frac{1}{4} + \frac{{ - 4}}{5}\)

b) \(\frac{8}{{13}}.\frac{1}{4} + \frac{8}{{13}}.\frac{3}{4} + \frac{5}{{13}}\)

c) \(\left| {\frac{{ - 3}}{2}} \right|.\sqrt {64}  - 0,125:\frac{3}{8} + {\left( { - 2024} \right)^0}\)

Bài 2. (1,5 điểm) Cho hai đa thức: \(P\left( x \right) =  - 2{x^2} - 5x - 2\)

                                             và \(Q\left( x \right) =  - 2{x^4} - 5{x^3} + 10x - 17{x^2} + 4{x^3} - 5 + {x^3}\).

a) Thu gọn đa thức \(Q\left( x \right)\) rồi sắp xếp theo luỹ thừa giảm dần của biến.

b) Tính \(P\left( x \right) + Q\left( x \right)\).

c) Chứng tỏ \(x =  - 2\) là nghiệm của \(P\left( x \right)\).

Bài 3. (1 điểm) Biểu đồ hình quạt ở hình bên biểu diễn kết quả điều tra (tính theo tỉ số phần trăm) chọn các màu ưa thích nhất trong bốn màu: xanh, đỏ, tím, trắng của học sinh khối 7. Mỗi học sinh chỉ được chọn một màu sắc khi được hỏi ý kiến.

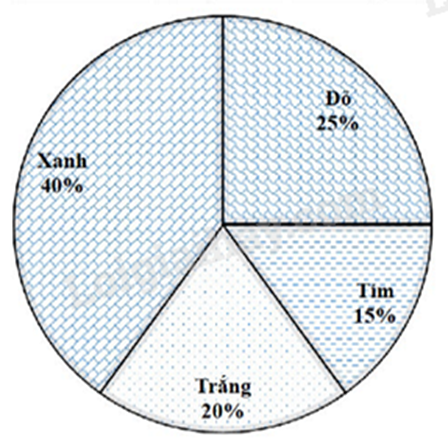
a) Lập bảng thống kê biểu diễn tỉ lệ học sinh yêu thích mỗi màu.

b) Biết rằng tổng số học sinh khối 7 là 120 em. Hỏi có bao nhiêu học sinh yêu thích màu xanh?

Bài 4. (3 điểm) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H. Lấy N là trung điểm của cạnh AC, hai đoạn thẳng BN và AH cắt nhau tại G. Trên tia đối của tia NG lấy điểm K sao cho NK = NG.

a) Chứng minh \(\Delta ABH = \Delta ACH\).

b) Chứng minh \(CK \bot BC\).

c) Gọi I là giao điểm của KH và CG. Chứng minh I là trọng tâm của \(\Delta BCK\).

d) Gọi M là trung điểm của cạnh AB. Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Căn bậc hai số học của số 9 là:

A. 3.

B. -3.

C. 9.

D. -9.

Phương pháp

Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của một số a không âm là \(\sqrt a \).

Lời giải

Căn bậc hai số học của 9 là \(\sqrt 9  = 3\).

Đáp án: A.

Câu 2: Số nào dưới đây là số thập phân vô hạn tuần hoàn?

A. \(\sqrt {144} \).

B. \(2,\left( 3 \right)\).

C. \( - 1,2345\).

D. \(\pi  = 3,141592653589...\).

Phương pháp

Phân biệt số nguyên, số thập phân hữu hạn, vô hạn tuần hoàn, vô hạn không tuần hoàn.

Lời giải

Ta có:

\(\sqrt {144}  = 12\) nên là số nguyên.

2,(3) là số thập phân vô hạn tuần hoàn với chu kì là 3.

-1,2345 là số thập phân hữu hạn.

\(\pi  = 3,141592653589...\) là số thập phân vô hạn không tuần hoàn.

Đáp án: B.

Câu 3: Chữ số a thích hợp để \( - 12,6a\left( {456} \right) <  - 12,69321\) là

A. 7.

B. 9.

C. 8.

D. 6.

Phương pháp

Viết chu kì của số \( - 12,6a\left( {456} \right)\) thành dạng đầy đủ, so sánh lần lượt các chữ số từ trái sang phải.

Lời giải

Ta có: \( - 12,6a\left( {456} \right) =  - 12,6a456456...\)

Vì \( - 12,6a456456... <  - 12,69321\) nên \(12,6a456456... > 12,69321\)

Do đó \(a456456... > 9321\) nên \(a = 9\) (vì 4 > 3).

Đáp án: B.

Câu 4: Cho \(\left| x \right| = 4\) thì giá trị của \(x\) là:

A. \(x = 4\).

B. \(x =  - 2\).

C. \(x = 2\) hoặc \(x =  - 2\).

D. \(x = 4\) hoặc \(x =  - 4\).

Phương pháp

Nếu \(\left| x \right| = a\) thì \(x = a\) hoặc \(x =  - a\).

Lời giải

Vì \(\left| x \right| = 4\) nên \(x = 4\) hoặc \(x =  - 4\).

Đáp án: D.

Câu 5: Hai góc kề bù là

A. hai góc vừa kề nhau, vừa bù nhau.

B. hai góc có tổng số đo bằng \(90^\circ \).

C. hai góc có tổng số đo bằng \(180^\circ \).

D. hai góc có chung đỉnh.

Phương pháp

Dựa vào khái niệm về hai góc kề bù.

Lời giải

Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau nên đáp án A đúng.

Hai góc có tổng số đo bằng \(180^\circ \) chưa chắc đã kề nhau nên đáp án C sai.

Đáp án: A.

Câu 6: Tia Ot nào trong các hình dưới đây là tia phân giác của góc \(xOy\)?

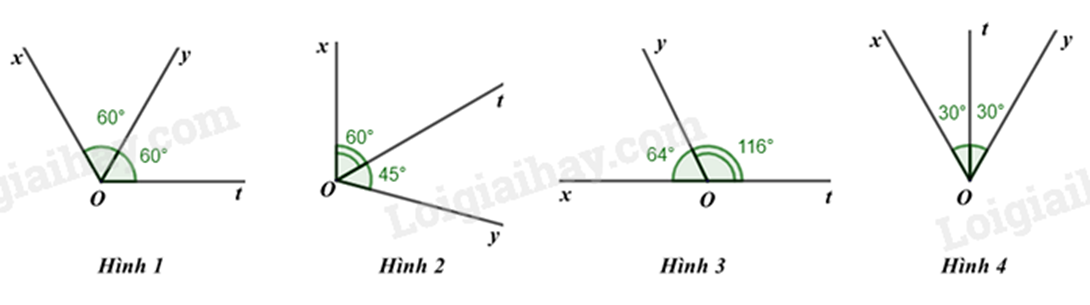
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Phương pháp

Tia nằm giữa 2 cạnh của một góc và tạo với 2 cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

Lời giải

Tia Ot là tia phân giác của góc \(xOy\) thì

+) Ot nằm giữa Ox và Oy, loại Hình 1, Hình 3.

+) \(\widehat {xOt} = \widehat {tOy}\) nên Hình 2 không thoả mãn.

Ta chọn Hình 4.

Đáp án: D.

Câu 7: Dừa sáp là một trong những đặc sản lại, quý hiếm có giá trị dinh dưỡng cao được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng. Nếu mua \(x\left( {x \in \mathbb{N}} \right)\) quả dừa sáp thì người mua phải trả số tiền (đồng) là:

A. \(200000x\).

B. \(200000\).

C. \(200000 + x\).

D. \(\frac{{200000}}{x}\).

Phương pháp

Vì số tiền phải trả và số quả tỉ lệ thuận với nhau nên ta viết được giá tiền theo \(x\).

Lời giải

Vì số tiền phải trả và số quả tỉ lệ thuận với nhau nên ta có:

Số tiền phải trả = 200 000\(x\).

Đáp án: A.

Câu 8: Cho đa thức \(B\left( x \right) = 2{x^2} + 5x + 2\). Trong các số sau, số nào là nghiệm của đa thức đã cho.

A. \(x = 2\).

B. \(x = 1\).

C. \(x =  - 1\).

D. \(x =  - 2\).

Phương pháp

Thay lần lượt các giá trị của \(x\) vào \(B\left( x \right)\), giá trị nào làm cho \(B\left( x \right) = 0\) thì là nghiệm của đa thức.

Lời giải

Thay \(x = 2\) vào \(B\left( x \right)\), ta được: \(B\left( 2 \right) = {2.2^2} + 5.2 + 2 = 20\) nên \(x = 2\) không phải nghiệm của \(B\left( x \right)\).

Thay \(x = 1\) vào \(B\left( x \right)\), ta được: \(B\left( 1 \right) = {2.1^2} + 5.1 + 2 = 9\) nên \(x = 1\) không phải nghiệm của \(B\left( x \right)\).

Thay \(x =  - 1\) vào \(B\left( x \right)\), ta được: \(B\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} + 5.\left( { - 1} \right) + 2 =  - 1\) nên \(x =  - 1\) không phải nghiệm của \(B\left( x \right)\).

Thay \(x =  - 2\) vào \(B\left( x \right)\), ta được: \(B\left( 2 \right) = 2.{\left( { - 2} \right)^2} + 5.\left( { - 2} \right) + 2 = 0\) nên \(x =  - 2\) là nghiệm của \(B\left( x \right)\).

Đáp án: D.

Câu 9: Cho hình vẽ bên.

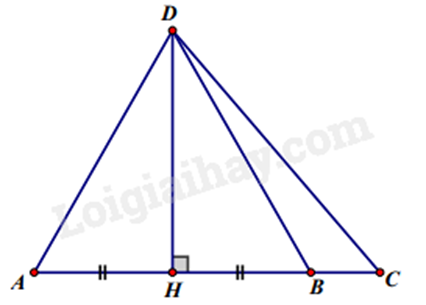
Chọn khẳng định sai trong các khẳng định sau:

A. DA > DH.

B. DC < DH.

C. DA = DB.

D. HB < HC.

Phương pháp

Sử dụng kiến thức về đường vuông góc và đường xiên để kiểm tra A, B.

Chứng minh tam giác bằng nhau để kiểm tra C.

Sử dụng kiến thức về hình chiếu.

Lời giải

Ta có:

DA > DH (đường xiên > đường vuông góc) nên A đúng.

DC  > DH (đường xiên > đường vuông góc) nên B sai.

DA = DB (chứng minh \(\Delta DAH = \Delta DBH\) (c.g.c)) nên C đúng.

Do DB < DC nên HB < HC (hình chiếu của DB và DC) nên D đúng.

Đáp án: B.

Câu 10: Các đường phân giác của tam giác ABC cắt nhau tại D thì

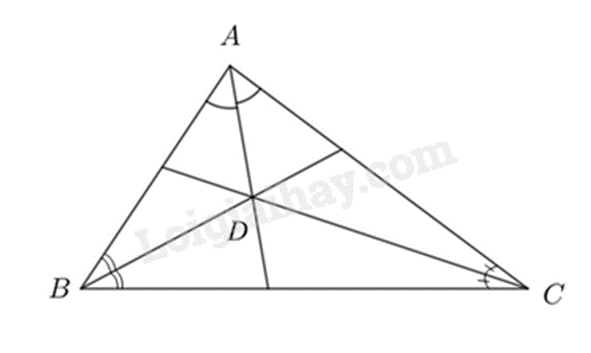
A. điểm D cách đều ba cạnh của tam giác ABC.

B. điểm D là trọng tâm của tam giác ABC.

C. điểm D là trực tâm của tam giác ABC.

D. điểm D cách đều ba đỉnh A, B, C.

Phương pháp

Sử dụng kiến thức về sự đồng quy của ba đường phân giác.

Lời giải

Vì D là giao điểm của ba đường phân giác trong tam giác ABC nên điểm D cách đều ba cạnh của tam giác ABC.

Đáp án: A.

Câu 11: Bạn An làm một chiếc hộp đựng quà hình lập phương có cạnh bằng 10 cm. Bỏ qua các mép gấp, diện tích giấy mà bạn An cần dùng là

A. \(60c{m^2}\).

B. \(100c{m^2}\).

C. \(600c{m^2}\).

D. \(1000c{m^2}\).

Phương pháp

Diện tích giấy mà bạn An cần dùng chính là diện tích toàn phần của hình lập phương.

Diện tích toàn phần của hình lập phương bằng \(6{a^2}\) (với a là cạnh của hình lập phương).

Lời giải

Diện tích giấy mà bạn An cần dùng chính là diện tích toàn phần của hình lập phương.

Diện tích giấy mà bạn An cần dùng là: \({6.10^2} = 600\left( {c{m^2}} \right)\)

Đáp án: C.

Câu 12: Một thanh socola hình lăng trụ đứng tam giác có các kích thước như hình vẽ. Thể tích của thanh socola đó là

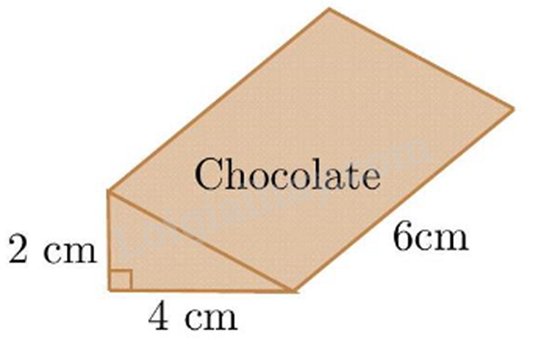
A. \(12c{m^3}\).

B. \(24c{m^3}\).

C. \(36c{m^3}\).

D. \(48c{m^3}\).

Phương pháp

Thể tích của hình lăng trụ đứng bằng S_đáy.chiều cao.

Diện tích hình tam giác vuông bằng \(\frac{1}{2}\). tích hai cạnh góc vuông.

Lời giải

Diện tích đáy của thanh socola đó là:

\(\frac{1}{2}.2.4 = 4\left( {c{m^2}} \right)\).

Thể tích của thanh socola đó là:

\(4.6 = 24\left( {c{m^3}} \right)\)

Đáp án: B.

Phần tự luận.

Bài 1. (1,5 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \(\frac{1}{4} + \frac{{ - 4}}{5}\)

b) \(\frac{8}{{13}}.\frac{1}{4} + \frac{8}{{13}}.\frac{3}{4} + \frac{5}{{13}}\)

c) \(\left| {\frac{{ - 3}}{2}} \right|.\sqrt {64}  - 0,125:\frac{3}{8} + {\left( { - 2024} \right)^0}\)

Phương pháp

Sử dụng quy tắc cộng, trừ, nhân, chia với số thực.

Lời giải

a) \(\frac{1}{5} + \frac{{ - 4}}{5} = \frac{{1 + \left( { - 4} \right)}}{5} = \frac{{ - 3}}{5}\)

b) \(\frac{8}{{13}}.\frac{1}{4} + \frac{8}{{13}}.\frac{3}{4} + \frac{5}{{13}}\)

\(\begin{array}{l} = \frac{8}{{13}}\left( {\frac{1}{4} + \frac{3}{4}} \right) + \frac{5}{{13}}\\ = \frac{8}{{13}} + \frac{5}{{13}}\\ = \frac{{13}}{{13}} = 1\end{array}\)

c) \(\left| {\frac{{ - 3}}{2}} \right|.\sqrt {64}  - 0,125:\frac{3}{8} + {\left( { - 2024} \right)^0}\)

\(\begin{array}{l} = \frac{3}{2}.8 - 0,125.\frac{8}{3} + 1\\ = 12 - \frac{1}{3} + 1\\ = 12\end{array}\)

Bài 2. (1,5 điểm) Cho hai đa thức: \(P\left( x \right) =  - 2{x^2} - 5x - 2\)

                                             và \(Q\left( x \right) =  - 2{x^4} - 5{x^3} + 10x - 17{x^2} + 4{x^3} - 5 + {x^3}\).

a) Thu gọn đa thức \(Q\left( x \right)\) rồi sắp xếp theo luỹ thừa giảm dần của biến.

b) Tính \(P\left( x \right) + Q\left( x \right)\).

c) Chứng tỏ \(x =  - 2\) là nghiệm của \(P\left( x \right)\).

Phương pháp

a) Thực hiện cộng, trừ các đơn thức cùng mũ để thu gọn đa thức.

b) Để cộng (hay trừ) hai đa thức, ta làm như sau:

Bước 1: Viết hai đa thức trong dấu ngoặc

Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc)

Bước 3: Nhóm các hạng tử đồng dạng

Bước 4: Cộng, trừ các đơn thức đồng dạng.

b) Thay \(x =  - 2\) vào đa thức \(P\left( x \right)\), \(P\left( 2 \right) = 0\) thì \(x =  - 2\) là nghiệm của \(P\left( x \right)\).

Lời giải

a) Ta có:

\(\begin{array}{l}Q\left( x \right) =  - 2{x^4} - 5{x^3} + 10x - 17{x^2} + 4{x^3} - 5 + {x^3}\\ =  - 2{x^4} + \left( { - 5{x^3} + 4{x^3} + {x^3}} \right) - 17{x^2} + 10x - 5\\ =  - 2{x^4} - 17{x^2} + 10x - 5\end{array}\)

b) Ta có:

\(\begin{array}{l}P\left( x \right) + Q\left( x \right)\\ = \left( { - 2{x^2} - 5x - 2} \right) + \left( { - 2{x^4} - 17{x^2} + 10x - 5} \right)\\ =  - 2{x^2} - 5x - 2 - 2{x^4} - 17{x^2} + 10x - 5\\ =  - 2{x^4} + \left( { - 2{x^2} - 17{x^2}} \right) + \left( { - 5x + 10} \right) + \left( { - 2 - 5} \right)\\ =  - 2{x^4} - 19{x^2} + 5x - 7\end{array}\)

c) Thay \(x =  - 2\) vào đa thức \(P\left( x \right)\), ta được: \( - 2.{\left( { - 2} \right)^2} - 5\left( { - 2} \right) - 2 =  - 2.4 + 10 - 2 =  - 8 + 10 - 2 = 0\) nên \(x =  - 2\) là nghiệm của đa thức \(P\left( x \right)\).

Bài 3. (1 điểm) Biểu đồ hình quạt ở hình bên biểu diễn kết quả điều tra (tính theo tỉ số phần trăm) chọn các màu ưa thích nhất trong bốn màu: xanh, đỏ, tím, trắng của học sinh khối 7. Mỗi học sinh chỉ được chọn một màu sắc khi được hỏi ý kiến.

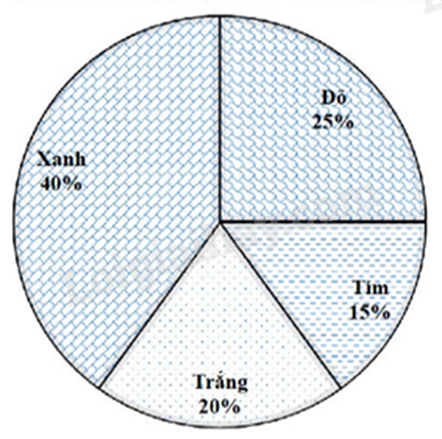
a) Lập bảng thống kê biểu diễn tỉ lệ học sinh yêu thích mỗi màu.

b) Biết rằng tổng số học sinh khối 7 là 120 em. Hỏi có bao nhiêu học sinh yêu thích màu xanh?

Phương pháp

a) Quan sát biểu đồ để lập bảng thống kê.

b) Số học sinh yêu thích màu xanh = tổng số học sinh . tỉ lệ phần trăm tương ứng với màu xanh.

Lời giải

a) Ta có bảng thống kê sau:

b) Số học sinh thích màu xanh là: \(120.40\%  = 48\) (em)

Bài 4. (3 điểm) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H. Lấy N là trung điểm của cạnh AC, hai đoạn thẳng BN và AH cắt nhau tại G. Trên tia đối của tia NG lấy điểm K sao cho NK = NG.

a) Chứng minh \(\Delta ABH = \Delta ACH\).

b) Chứng minh \(CK \bot BC\).

c) Gọi I là giao điểm của KH và CG. Chứng minh I là trọng tâm của \(\Delta BCK\).

d) Gọi M là trung điểm của cạnh AB. Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\).

Phương pháp

Dựa vào giả thiết để vẽ hình.

a) Chứng minh \(\Delta ABH = \Delta ACH\) theo trường hợp cạnh huyền - cạnh góc vuông.

b) Chứng minh \(\Delta AGN = \Delta CKN\left( {c.g.c} \right)\) suy ra hai góc bằng nhau.

Mà hai góc bằng nhau đó ở vị trí so le trong nên suy ra AG // CK hay AH // CK.

Kết hợp với AH \( \bot \) BC nên \(CK \bot BC\).

c) Chứng minh G là trung điểm của BK; H là trung điểm của BC nên có hai đường trung tuyến cắt nhau tại I.

Do đó I là trọng tâm của tam giác BCK.

d) Chứng minh GM = GN

Chứng minh \(GN = \frac{1}{4}BK\)

Chứng minh \(BK < BC + CK\)

Chứng minh AG = CK (6)

Kết hợp lại ta được điều phải chứng minh

Lời giải

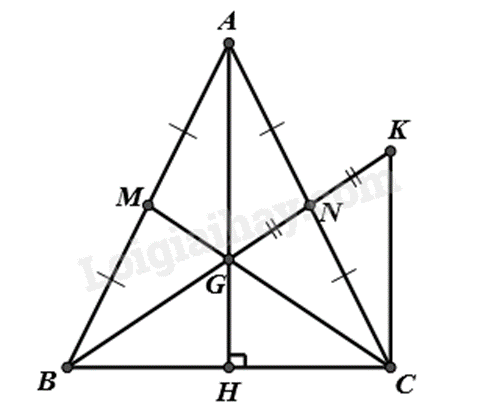
a) Vì tam giác ABC cân tại A nên AB = AC.

Vì \(AH \bot BC\) nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \).

Xét \(\Delta ABH\) và \(\Delta ACH\) có:

\(AB = AC\)

\(\widehat {AHB} = \widehat {AHC}\left( { = 90^\circ } \right)\)

AH chung

nên \(\Delta ABH = \Delta ACH\) (cạnh huyền – cạnh góc vuông)

b) Xét \(\Delta AGN\) và \(\Delta CKN\) có:

\(AN = NC\) (N là trung điểm của AC)

\(\widehat {ANG} = \widehat {CNK}\) (hai góc đối đỉnh)

\(GN = NK\) (gt)

nên \(\Delta AGN = \Delta CKN\left( {c.g.c} \right)\)

suy ra \(\widehat {AGN} = \widehat {CKN}\).

Mà hai góc này ở vị trí so le trong nên AG // CK hay AH // CK.

Mà \(AH \bot BC\) nên \(CK \bot BC\).

c)

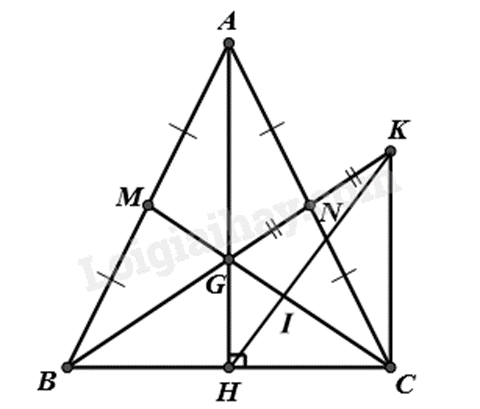
Vì \(\Delta ABH = \Delta ACH\) nên BH = CH, mà \(H \in BC\) suy ra H là trung điểm của BC.

Do đó AH là đường trung tuyến của tam giác ABC.

Vì N là trung điểm của AC nên BN là đường trung tuyến của tam giác ABC.

Mà BN cắt AH tại G nên G là trọng tâm của tam giác ABC.

Suy ra \(BG = \frac{2}{3}BN\) và \(GN = \frac{1}{3}BN\), do đó \(BG = 2GN\) (1)

Vì NK = NG và \(N \in GK\) nên N là trung điểm của GK, suy ra \(GK = 2GN\) (2)

Từ (1) và (2) suy ra BG = KG.

Do đó G là trung điểm của BK.

Xét tam giác BCK có:

CG là đường trung tuyến (vì G là trung điểm của BK)

KH là đường trung tuyến (vì H là trung điểm của BC)

Mà KH cắt CG tại I

Do đó I là trọng tâm của tam giác BCK.

d) Vì tam giác ABC cân nên hai đường trung tuyến BN = CM, do đó GM = GN (3)

Mà \(GK = 2GN\) nên \(GN = \frac{1}{2}GK\).

Mà \(GK = \frac{1}{2}BK\) (vì G là trung điểm của BK) nên \(GN = \frac{1}{2}.\frac{1}{2}BK = \frac{1}{4}BK\) (4)

Áp dụng bất đẳng thức tam giác vào tam giác BCK, ta có: \(BK < BC + CK\) (5)

Vì \(\Delta AGN = \Delta CKN\left( {c.g.c} \right)\) nên AG = CK (6)

Từ (3), (4), (5) và (6) suy ra \(GM < \frac{1}{4}\left( {BC + CK} \right) = \frac{1}{4}\left( {BC + AG} \right)\)

Vậy \(GM < \frac{1}{4}\left( {BC + AG} \right)\)