Dạng bài toán thực tế - Ôn hè Toán 7 lên 8

Lý thuyết

Để giải quyết được những bài toán thực tế liên quan đến số hữu tỉ, ta thường làm như sau:

Bước 1: Phân tích bài toán, từ các dữ kiện đề bài xác định các giá trị của cùng một đại lượng (ví dụ: các giá trị của một đoạn đường, một chiếc bánh, một quyển sách, một đơn vị thời gian...) và thiết lập mối quan hệ giữa các đại lượng trong bài toán.

Bước 2: Dựa vào quy tắc cộng, trừ, nhân, chia số hữu tỉ, thực hiện các phép toán tương ứng.

Một số kiến thức liên quan:

+ Phép tính cộng, trừ, nhân, chia số hữu tỉ.

+ Quy tắc bỏ dấu ngoặc.

+ So sánh các số hữu tỉ.

+ Lũy thừa với số mũ tự nhiên của một số hữu tỉ (định nghĩa, nhân, chia hai lũy thừa cùng cơ số, lũy thừa của lũy thừa).

+ Thứ tự thực hiện các phép tính.

+ Quy tắc chuyển vế.

Bước 3: Kết luận.

Bài tập

Bài 1: Hình vẽ mô phỏng vị trí của năm điểm A, B, C, D, E so với mực nước biển. Biết rằng độ cao (tính

theo đơn vị ki – lô - mét) so với mực nước biển của mỗi điểm là một trong các số sau:

\(\frac{{33}}{{12}};\frac{{79}}{{30}}; - \frac{{25}}{{12}}; - \frac{5}{6};0\)

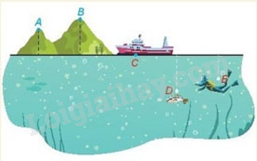
Quan sát hình và cho biết độ cao của mỗi điểm?

Bài 2: Ông A gửi tiền tiết kiệm 200 000 000 đồng vào ngân hàng theo thể thức kì hạn 1 năm. Hết thời hạn ông A nhận được cả vốn lẫn lãi là 214 400 000 đồng. Tính lãi suất ngân hàng theo thể thức này?

Bài 3: Một người đi quãng đường từ địa điểm A đến địa điểm B với vận tốc 30 km/h mất 3,5 giờ. Từ địa điểm B quay trở về dịa điểm A, người đó đi với vận tốc 36 km/h. Tính thời gian đi từ địa điểm B quay về địa điểm A của người đó?

Bài 4: Vào dịp tết nguyên đán, bà của An gói bánh chưng cho gia đình. Nguyên liệu để làm bánh gồm gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,8kg khoảng gồm 0,5kg gạo; 0,125kg đậu xanh, 0,04kg lá dong, còn lại là thịt. Hỏi khối lượng thịt trong mỗi cái bánh là khoảng bao nhiêu?

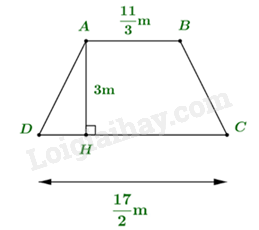
Bài 5: Tính diện tích hình thang ABCD có kích thước như hình sau:

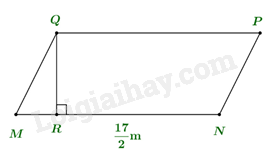
Bài 6: Hình bình hành MNPQ có \(MN = \frac{{17}}{2}m\) và diện tích bằng \(\frac{{73}}{4}{m^2}\). Tính đường cao QR của hình bình hành?

Bài 7: Trong đợt tri ân khách hàng, một cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách mua hàng. Cửa hàng vẫn lãi được 20% của giá nhập về đối với mỗi chiếc xe bán ra. Tính giá nhập về và giá niêm yết của một chiếc xe đạp, biết rằng với mỗi chiếc xe đạp bán ra như thế, cửa hàng vẫn lãi được 600 000 đồng?

Bài 8: Lúc 7 giờ An đi xe đạp từ A đến B với vận tốc 12 km/h. Cùng thời điểm đó thì Bình đi bộ từ B về A với vận tốc 5 km/h. Hai bạn gặp nhau tại điểm hẹn lúc 7 giờ 45 phút. Tính độ dài quãng đường AB?

Bài 9: Hai người thợ cùng làm một công việc. Nếu làm riêng thì người thứ nhất phải mất \(4\) giờ, người thứ hai phải mất \(6\) giờ mới hoàn thành công việc. hỏi nếu làm chung trong \(45\) phút thì hai người làm được mấy phần công việc?

Bài 10: Một công trường xây dựng cần chuyển về 35,7 tấn sắt. Lần đầu chở được \(\frac{4}{7}\) số sắt đó về bằng xe tải, mỗi xe tải chở được 1,7 tấn sắt, lần thứ hai chở hết số sắt còn lại với số xe tải bằng \(\frac{1}{2}\) số xe lúc đầu. Hỏi mỗi xe lúc sau chở được bao nhiêu tấn sắt?

--------Hết--------

Lời giải chi tiết:

Bài 1: Hình vẽ mô phỏng vị trí của năm điểm A, B, C, D, E so với mực nước biển. Biết rằng độ cao (tính

theo đơn vị ki – lô - mét) so với mực nước biển của mỗi điểm là một trong các số sau:

\(\frac{{33}}{{12}};\frac{{79}}{{30}}; - \frac{{25}}{{12}}; - \frac{5}{6};0\)

Quan sát hình và cho biết độ cao của mỗi điểm?

Phương pháp

So sánh các vị trí các điểm A, B, C, D, E trong hình.

So sánh các số hữu tỉ để xác định độ cao các điểm tương ứng.

Lời giải

Quan sát hình vẽ ta thấy chiều cao từ lớn đến bé lần lượt là B, A, C, E, D.

So sánh các số: Ta chia làm hai nhóm:

+ Các số lớn hơn 0: \(\frac{{33}}{{12}};\frac{{79}}{{30}}\)

\(\begin{array}{l}\frac{{33}}{{12}} = \frac{{11}}{4} = \frac{{165}}{{60}};\\\frac{{79}}{{30}} = \frac{{158}}{{60}}\end{array}\)

Vì 158 < 165 nên \(\frac{{158}}{{60}} < \frac{{165}}{{60}}\) hay \(\frac{{79}}{{30}} < \frac{{33}}{{12}}\) (1)

+ Các số nhỏ hơn 0: \( - \frac{{25}}{{12}}; - \frac{5}{6}\)

\( - \frac{{25}}{{12}} = \frac{{ - 25}}{{12}}; - \frac{5}{6} = \frac{{ - 10}}{{12}}\)

Vì \( - 25 <  - 10\) nên \(\frac{{ - 25}}{{12}} < \frac{{ - 10}}{{12}}\) hay \( - \frac{{25}}{{12}} <  - \frac{5}{6}\) (2)

Từ (1) và (2) suy ra các số theo thứ tự từ lớn đến bé là: \(\frac{{33}}{{12}};\frac{{79}}{{30}};0; - \frac{5}{6}; - \frac{{25}}{{12}}\)

Vậy độ cao của điểm A là \(\frac{{79}}{{30}}\); độ cao của điểm B là \(\frac{{33}}{{12}}\); độ cao của điểm C là 0; độ cao của điểm D là \( - \frac{{25}}{{12}}\); độ cao của điểm E là \( - \frac{5}{6}\).

Bài 2: Ông A gửi tiền tiết kiệm 200 000 000 đồng vào ngân hàng theo thể thức kì hạn 1 năm. Hết thời hạn ông A nhận được cả vốn lẫn lãi là 214 400 000 đồng. Tính lãi suất ngân hàng theo thể thức này?

Phương pháp

Tính tiền lãi một năm.
Tìm lãi suất theo tỉ số phần trăm.

Lời giải

Số tiền lãi ông A nhận được là:

\(214\,400\,000 - 200\,000\,000 = 14\,400\,000\) (đồng)

Lãi suất ngân hàng là:

\(14\,400\,000:200\,000\,000 = 7,2\% \).

Vậy lãi suất ngân hàng theo thể thức này là 7,2%.

Bài 3: Một người đi quãng đường từ địa điểm A đến địa điểm B với vận tốc 30 km/h mất 3,5 giờ. Từ địa điểm B quay trở về dịa điểm A, người đó đi với vận tốc 36 km/h. Tính thời gian đi từ địa điểm B quay về địa điểm A của người đó?

Phương pháp

Sử dụng công thức tính quãng đường theo vận tốc và thời gian:

S = v.t (S: quãng đường, v: vận tốc, t: thời gian)

Lời giải

Quãng đường AB dài là: \(30.3,5 = 105\left( {km} \right)\)

Thời gian người đó đi từ B đến A là: \(105:36 = 2\frac{{11}}{{12}}\) (giờ) = 2 giờ 55 phút.

Vậy thời gian đi từ địa điểm B quay về địa điểm A của người đó là 2 giờ 55 phút.

Bài 4: Vào dịp tết nguyên đán, bà của An gói bánh chưng cho gia đình. Nguyên liệu để làm bánh gồm gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,8kg khoảng gồm 0,5kg gạo; 0,125kg đậu xanh, 0,04kg lá dong, còn lại là thịt. Hỏi khối lượng thịt trong mỗi cái bánh là khoảng bao nhiêu?

Phương pháp

Sử dụng phép trừ số hữu tỉ để tính.

Lời giải

Khối lượng thịt trong mỗi cái bánh chưng là
\(0,8 - \left( {0,5 + 0,125 + 0,04} \right) = 0,8 - 0,665 = 0,135\left( {kg} \right)\)

Vậy khối lượng thịt trong mỗi cái bánh là khoảng 0,135kg.

Bài 5: Tính diện tích hình thang ABCD có kích thước như hình sau:

Phương pháp

Sử dụng công thức tính diện tích hình thang: \(S = \frac{1}{2}\) (tổng hai đáy).chiều cao.

Lời giải

Diện tích hình thang ABCD là:

\(\frac{1}{2}\left( {AB + CD} \right).AH = \frac{1}{2}\left( {\frac{{11}}{3} + \frac{{17}}{2}} \right).3 = \frac{1}{2}.\frac{{73}}{6}.3 = \frac{{73}}{4}\left( {{m^2}} \right)\)

Vậy diện tích hình thang ABCD là \(\frac{{73}}{4}{m^2}\).

Bài 6: Hình bình hành MNPQ có \(MN = \frac{{17}}{2}m\) và diện tích bằng \(\frac{{73}}{4}{m^2}\). Tính đường cao QR của hình bình hành?

Phương pháp

Từ công thức tính diện tích hình bình hành: S = đáy. chiều cao tương ứng để tính đường cao QR.

Lời giải

Diện tích của hình bình hành ABCD là S = MN.QR

Thay số, ta được: \(\frac{{73}}{4} = \frac{{17}}{2}.QR\)

Suy ra \(QR = \frac{{73}}{4}:\frac{{17}}{2} = \frac{{73}}{{34}}\left( m \right)\)

Vậy đường cao QR là \(\frac{{73}}{{34}}m\).

Bài 7: Trong đợt tri ân khách hàng, một cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách mua hàng. Cửa hàng vẫn lãi được 20% của giá nhập về đối với mỗi chiếc xe bán ra. Tính giá nhập về và giá niêm yết của một chiếc xe đạp, biết rằng với mỗi chiếc xe đạp bán ra như thế, cửa hàng vẫn lãi được 600 000 đồng?

Phương pháp

20% của giá nhập về tương ứng với 600000 đồng nên ta tính được giá nhập.

Tính số % giá niêm yết.

Từ đó tính giá niêm yết của chiếc xe đạp.

Lời giải

Cửa hàng lãi 20% của giá nhập về đối với mỗi chiếc xe đạp bán ra tương ứng với 600000 đồng.

Khi đó, giá nhập về của chiếc xe đạp là: 600000: 20% = 3000000 (đồng)

Cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách mua hàng, nghĩa là cửa hàng đó bán chiếc xe đạp bằng 100% - 25% = 75% giá niêm yết.

Khi đó, 75% giá niêm yết tương ứng với số tiền: 3000000 + 600000 = 3600000 (đồng)

Giá niêm yết của chiếc xe đạp là: 3600000: 75% = 4800000 (đồng)

Vậy giá nhập về của một chiếc xe đạp là 3000000 đồng và giá niêm yết của một chiếc xe đạp là 4800000 đồng.

Bài 8: Lúc 7 giờ An đi xe đạp từ A đến B với vận tốc 12 km/h. Cùng thời điểm đó thì Bình đi bộ từ B về A với vận tốc 5 km/h. Hai bạn gặp nhau tại điểm hẹn lúc 7 giờ 45 phút. Tính độ dài quãng đường AB?

Phương pháp

Tính thời gian An và Bình đi đến khi gặp nhau.

Tính quãng đường An đi, Bình đi: S = v.t (quãng đường = vận tốc.thời gian)

Quãng đường AB bằng tổng quãng đường An đi và Bình đi.

Lời giải

Thời gian An và Bình đi đến khi gặp nhau là: \(7\) giờ \(45\) phút - \(7\) giờ = \(45\) phút = \(\frac{3}{4}\)giờ.

Quãng đường An đi: \(12 \cdot \frac{3}{4} = 9\)(km)

Quãng đường Bình đi: \(5 \cdot \frac{3}{4} = \frac{{15}}{4}\) (km)

Độ dài quãng đường AB là: \(9 + \frac{{15}}{4} = \frac{{51}}{4} = 12,75\)(km)

Vậy độ dài quãng đường AB là 12,75km.

Bài 9: Hai người thợ cùng làm một công việc. Nếu làm riêng thì người thứ nhất phải mất \(4\) giờ, người thứ hai phải mất \(6\) giờ mới hoàn thành công việc. hỏi nếu làm chung trong \(45\) phút thì hai người làm được mấy phần công việc?

Phương pháp

Đổi \(45\) phút = \(\frac{3}{4}\)giờ

Tính lượng công việc người thứ nhất và người thứ hai làm được trong một giờ = 1 : số giờ.

Tính lượng công việc cả hai làm được trong một giờ.

Tính lượng công việc cả hai làm được trong \(\frac{3}{4}\) giờ.

Lời giải

Đổi \(45\) phút = \(\frac{3}{4}\)giờ

Một giờ người thứ nhất làm được \(\frac{1}{4}\) công việc

Một giờ người thứ hai làm được \(\frac{1}{6}\) công việc

Một giờ cả hai người làm được: \(\frac{1}{4} + \frac{1}{6} = \frac{5}{{12}}\) (công việc)

Trong \(\frac{3}{4}\) giờ cả hai người làm được: \(\frac{3}{4}.\frac{5}{{12}} = \frac{5}{{16}}\) (công việc)

Vậy trong \(45\) phút cả hai người làm được \(\frac{5}{{16}}\) công việc.

Bài 10: Một công trường xây dựng cần chuyển về 35,7 tấn sắt. Lần đầu chở được \(\frac{4}{7}\) số sắt đó về bằng xe tải, mỗi xe tải chở được 1,7 tấn sắt, lần thứ hai chở hết số sắt còn lại với số xe tải bằng \(\frac{1}{2}\) số xe lúc đầu. Hỏi mỗi xe lúc sau chở được bao nhiêu tấn sắt?

Phương pháp

Tính số tấn sắt lần đầu chở được = \(\frac{4}{7}\) số tấn sắt ban đầu.

Tính số tấn sắt lần thứ hai chở = số tấn sắt ban đầu – số tần sát lần đầu chở.

Tính số xe tải sử dụng lần đầu = số tần sắt lần đầu chở : số tấn sắt mỗi xe tải chở.

Tính số xe tải sử dụng lần thứ hai = \(\frac{1}{2}\) số xe tải sử dụng lần đầu.

Lời giải

Số tấn sắt lần đầu chở được là: \(35,7.\frac{4}{7} = 20,4\) (tấn)

Số tấn sắt chở lần hai là: \(35,7 - 20,4 = 15,3\) (tấn)

Số xe tải sử dụng lần đầu là: \(20,4:1,7 = 12\)(xe)

Số xe tải sử dụng lần hai là: \(12.\frac{1}{2} = 6\)(xe)

Mỗi xe lúc sau chở được số tấn sắt là: \(15,3:6 = 2,55\)(tấn)

Vậy mỗi xe lúc sau chở được 2,55 tấn sắt.