Dạng bài các góc ở vị trí đặc biệt - Ôn hè Toán 7 lên 8

Lý thuyết

Dạng 1. Các góc ở vị trí đặc biệt

A. Lý thuyết

* Hai góc kề nhau

Hai góc kề nhau là hai góc có chung đỉnh và chung 1 cạnh, hai cạnh còn lại nằm về 2 phía của đường thẳng chứa cạnh chung đó.

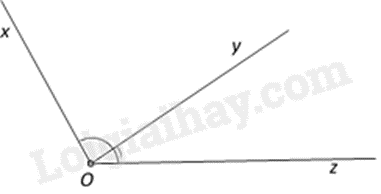
* Hai góc bù nhau

Hai góc bù nhau là hai góc có tổng số đo của hai góc là 180°.

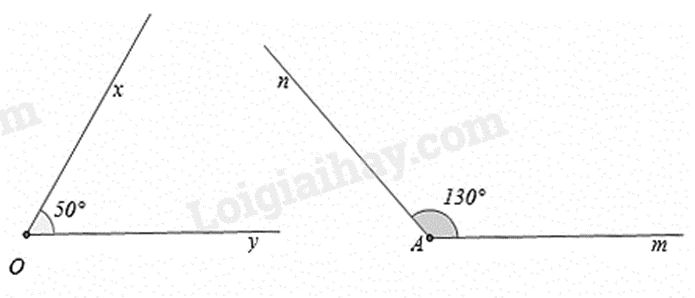
* Hai góc kề bù

- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

Ở hình bên, \(\widehat {xOz}\) và \(\widehat {yOz}\) là hai góc kề bù.

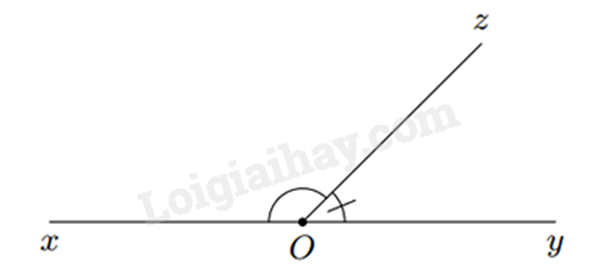
- Tính chất: Hai góc kề bù có tổng số đo bằng \(180^\circ \).

Chú ý:

- Hai góc kề bù còn được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó:

+ Hai góc kề nhau là hai góc có một cạch chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó.

+ Hai góc bù nhau là hai góc có tổng số đo bằng \(180^\circ \).

- Nếu điểm M nằm trong \(\widehat {xOy}\) thì ta nói tia OM nằm giữa hai cạnh (hai tia) Ox và Oy của \(\widehat {xOy}\). Khi đó, ta có:

\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\).

* Hai góc đối đỉnh

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

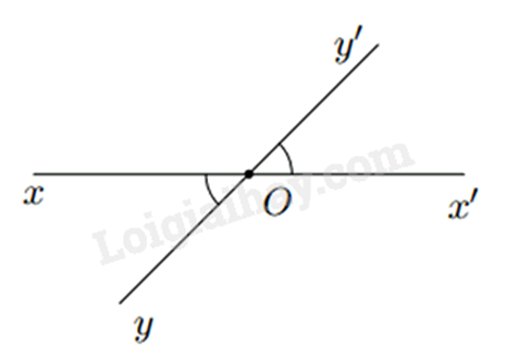
- Tính chất: Hai góc đối đỉnh thì bằng nhau.

Chú ý: Hai đường thẳng \(xx',yy'\) cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc. Kí hiệu là \(xx' \bot yy'\).

* Các góc tạo bởi một đường thẳng cắt hai đường thẳng

- Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A, bốn góc đỉnh B được đánh số thứ tự như hình bên.

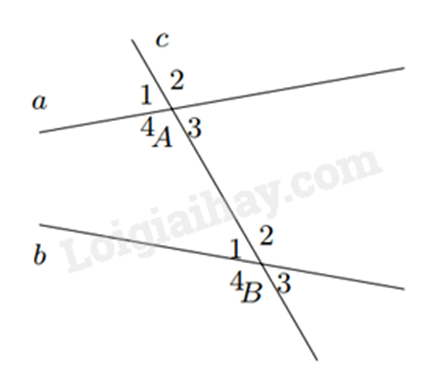
+ Các cặp góc \(\widehat {{A_3}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\) gọi là các cặp góc so le trong.

+ Các cặp góc \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_2}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_3}}\) và \(\widehat {{B_3}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_4}}\) gọi là các cặp góc đồng vị.

- Tính chất: Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

+ Hai góc so le trong còn lại bằng nhau.

+ Hai góc đồng vị bằng nhau.

Bài tập

Bài 1: Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:

A. \(\widehat {z'At'}\).

B. \(\widehat {z'At}\).

C. \(\widehat {zAt'}\).

D. \(\widehat {zAt}\).

Bài 2: Cho 2 đường thẳng ab và cd cắt nhau tại M (tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\)?

A. \(30^\circ \).

B. \(36^\circ \).

C. \(144^\circ \).

D. \(150^\circ \).

Bài 3: Cho \(\widehat {ABC} = 56^\circ \). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).

A. 124^o.

B. 142^o.

C. 65^o.

D. 56^o.

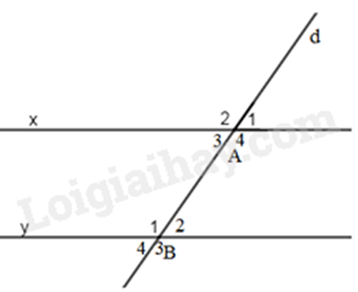
Bài 4: Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = 35^\circ \). Tính số đo của cặp góc so le trong còn lại.

A. \(115^\circ \).

B. \(55^\circ \).

C. \(135^\circ \).

D. \(145^\circ \).

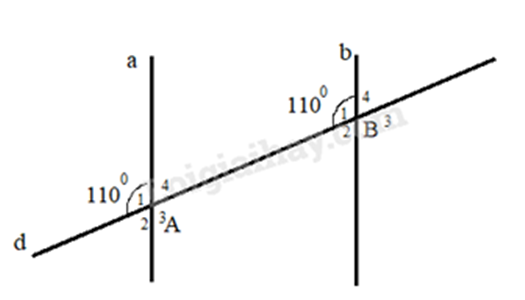
Bài 5: Cho hình vẽ dưới đây:

A. \(\widehat {{A_2}} = \widehat {{B_4}}\).

B. \(\widehat {{A_3}} = \widehat {{B_2}}\).

C. \(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \).

D. \(\widehat {{B_2}} = \widehat {{B_4}}\).

Bài 6: Cho \(\widehat {xBy}\) có số đo bằng \(60^\circ \). Vẽ góc đối đỉnh với \(\widehat {xBy}\). Góc này có số đo bằng bao nhiêu độ?

Bài 7: Cho hai góc kề nhau \(\widehat {xOy}\) và \(\widehat {yOz}\) có tổng số đo bằng \(150^\circ \) và \(\widehat {xOy} - \widehat {yOz} = 90^\circ \).

a) Tính số đo \(\widehat {xOy}\) và \(\widehat {yOz}\).

b) Vẽ các tia \(Ox',Oy'\) lần lượt là các tia đối của các tia \(Ox,Oy\). Tìm số đo \(\widehat {x'Oy'},\widehat {xOy'}\).

Bài 8: Hai đường thẳng MN và PQ cắt nhau tại A tạo thành MAP có số đo bằng \(30^\circ \).

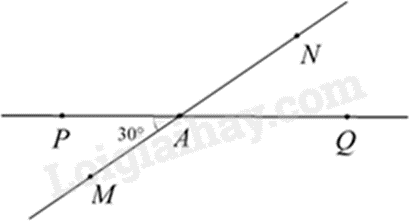
a) Tính số đo góc NAQ.

b) Tính số đo góc MAQ.

c) Viết tên các cặp góc đối đỉnh.

d) Viết tên các cặp góc kề bù.

Bài 9: Tính số đo các góc còn lại trong hình vẽ sau:

Bài 10: Cho hình vẽ:

a) Kể tên các cặp góc so le trong, các cặp góc đồng vị.

b) Tính \(\widehat {{M_4}} + \widehat {{N_3}};\widehat {{M_3}} + \widehat {{N_1}}\).

--------Hết--------

Lời giải chi tiết:

Bài 1: Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:

A. \(\widehat {z'At'}\).

B. \(\widehat {z'At}\).

C. \(\widehat {zAt'}\).

D. \(\widehat {zAt}\).

Phương pháp

Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).

Lời giải

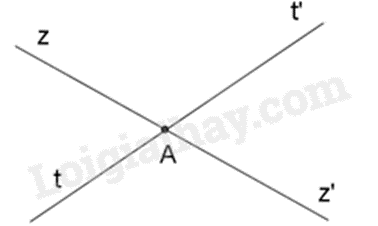
Vì hai đường thẳng zz'  và tt'  cắt nhau tại \(A\)  nên Az'  là tia đối của tia Az,At' là tia đối của tia At. Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).

Đáp án: B

Bài 2: Cho 2 đường thẳng ab và cd cắt nhau tại M (tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\)?

A. \(30^\circ \).

B. \(36^\circ \).

C. \(144^\circ \).

D. \(150^\circ \).

Phương pháp

Tổng hai góc kề bù bằng \(180^\circ \).

Lời giải

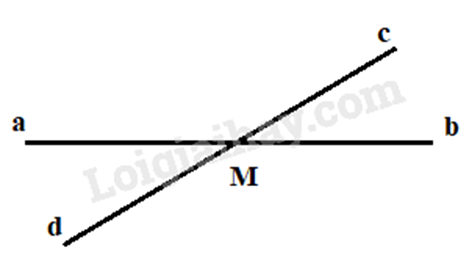
Ta có: \(\widehat {aMc} + \widehat {bMc} = 180^\circ \) (2 góc kề bù)

Mà \(\widehat {aMc} = 5.\widehat {bMc}\)

\(\begin{array}{*{20}{l}}{5.\widehat {bMc} + \widehat {bMc} = 180^\circ }\\{6.\widehat {bMc} = 180^\circ }\\{\widehat {bMc} = 180^\circ :6 = 30^\circ }\\{\widehat {aMc} = 5.30^\circ {\rm{\;}} = 150^\circ }\end{array}\)

\(\begin{array}{*{20}{l}}{5.\widehat {bMc} + \widehat {bMc} = 180^\circ }\\{6.\widehat {bMc} = 180^\circ }\\{\widehat {bMc} = 180^\circ :6 = 30^\circ }\\{\widehat {aMc} = 5.30^\circ {\rm{\;}} = 150^\circ }\end{array}\)

Đáp án: D

Bài 3: Cho \(\widehat {ABC} = 56^\circ \). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).

A. 124^o.

B. 142^o.

C. 65^o.

D. 56^o.

Phương pháp

Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc C'BA'.

Lời giải

Vì góc ABC'  kề bù với góc ABC  nên BC'  là tia đối của tia BC.

Vì góc C'BA'  kề bù với góc ABC'  nên BA'  là tia đối của tia BA.

Do đó, góc C'BA'  và góc ABC  đối đỉnh nên \(\widehat {C'BA'} = \widehat {ABC} = 56^\circ \). 

Đáp án: D

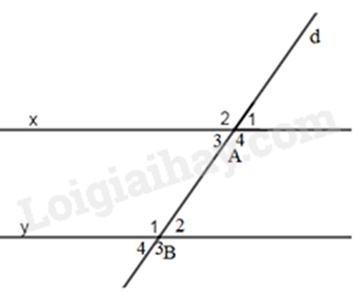
Bài 4: Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = 35^\circ \). Tính số đo của cặp góc so le trong còn lại.

A. \(115^\circ \).

B. \(55^\circ \).

C. \(135^\circ \).

D. \(145^\circ \).

Phương pháp

Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.

Lời giải

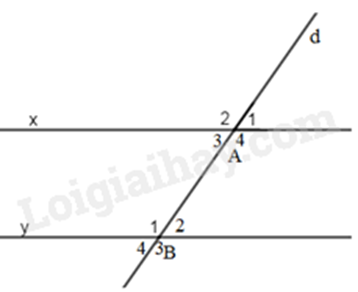
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = 180^\circ \) (kề bù)

suy ra \(\widehat {{A_4}} = 180^\circ  - \widehat {{A_3}} = 180^\circ  - 35^\circ  = 145^\circ \)

Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong

 Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1 cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = 35^\circ \) nên cặp góc so le trong còn lại cũng bằng nhau

Suy ra \(\widehat {{A_4}} = \widehat {{B_1}} = 145^\circ \).

Đáp án: D

Bài 5: Cho hình vẽ dưới đây:

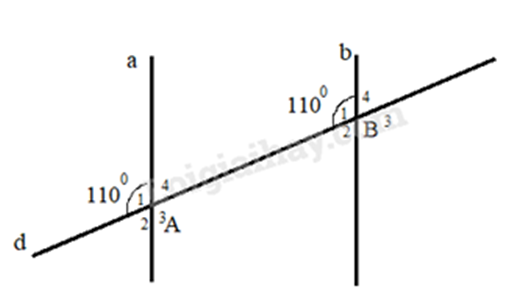
A. \(\widehat {{A_2}} = \widehat {{B_4}}\).

B. \(\widehat {{A_3}} = \widehat {{B_2}}\).

C. \(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \).

D. \(\widehat {{B_2}} = \widehat {{B_4}}\).

Phương pháp

Dựa vào tính chất các góc tạo bởi một đường thẳng cắt 2 đường thẳng.

Lời giải

Vì đường thẳng d cắt 2 đường thẳng a và b tạo thành cặp góc A₁ và B₁ bằng nhau (cùng bằng \(110^\circ \)) nên:

+) \(\widehat {{A_2}} = \widehat {{B_2}}\) (2 góc đồng vị)

Mà \(\widehat {{B_2}} = \widehat {{B_4}}\) (2 góc đối đỉnh)

Suy ra \(\widehat {{A_2}} = \widehat {{B_4}}\) nên A đúng

+) \(\widehat {{A_3}} = \widehat {{B_3}}\) (2 góc đồng vị)

Mà \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) (2 góc kề bù) và \(\widehat {{A_1}} = \widehat {{A_3}}\); \(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh) nên \(\widehat {{B_2}} + 110^\circ {\rm{\;}} = 180^\circ \)

Suy ra \(\widehat {{B_2}} = 70^\circ \)

Ta thấy \(\widehat {{A_3}} \ne \widehat {{B_2}}\) nên B sai

+) \(\widehat {{A_1}} = \widehat {{B_1}}\left( { = 110^\circ } \right)\)

Mà \(\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \) (2 góc kề bù)

Suy ra \(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \) nên C đúng

Ta có: \(\widehat {{B_2}} = \widehat {{B_4}}\) (2 góc đối đỉnh) nên D đúng

Đáp án: B

Bài 6: Cho \(\widehat {xBy}\) có số đo bằng \(60^\circ \). Vẽ góc đối đỉnh với \(\widehat {xBy}\). Góc này có số đo bằng bao nhiêu độ?

Phương pháp

Sử dụng kiến thức: Hai góc đối đỉnh có số đo bằng nhau.

Lời giải

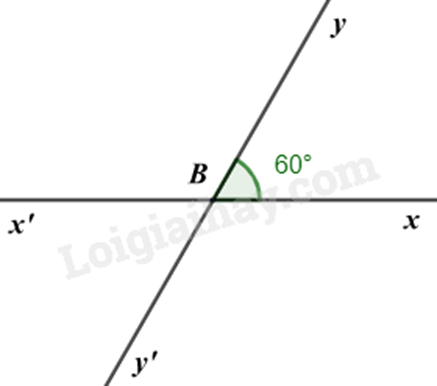
Vì \(\widehat {xBy}\) và \(\widehat {x'By'}\) là hai góc đối đỉnh nên \(\widehat {x'B'y} = \widehat {xBy} = 60^\circ \).

Bài 7: Cho hai góc kề nhau \(\widehat {xOy}\) và \(\widehat {yOz}\) có tổng số đo bằng \(150^\circ \) và \(\widehat {xOy} - \widehat {yOz} = 90^\circ \).

a) Tính số đo \(\widehat {xOy}\) và \(\widehat {yOz}\).

b) Vẽ các tia \(Ox',Oy'\) lần lượt là các tia đối của các tia \(Ox,Oy\). Tìm số đo \(\widehat {x'Oy'},\widehat {xOy'}\).

Phương pháp

a) Tính số đo hai góc khi biết tổng và hiệu của hai góc đó.

b) Sử dụng kiến thức về hai góc đối đỉnh và hai góc kề bù để tính các góc.

Lời giải

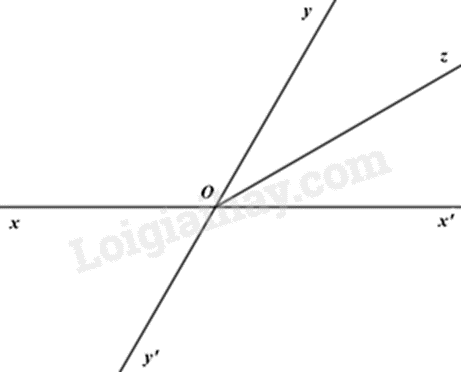
a) Ta có: \(\widehat {xOy} + \widehat {yOz} = 150^\circ ;\widehat {xOy} - \widehat {yOz} = 90^\circ \) nên \(\widehat {xOy} = \left( {150^\circ  + 90^\circ } \right):2 = 120^\circ \).

Suy ra \(\widehat {yOz} = 150^\circ  - 120^\circ  = 30^\circ \).

b) Vì tia \(Ox',Oy'\) lần lượt là các tia đối của các tia \(Ox,Oy\) nên \(\widehat {x'Oy'} = \widehat {xOy} = 120^\circ \).

Hai góc \(\widehat {xOy'}\) và \(\widehat {y'Ox'}\) là hai góc kề bù (do \(Ox\) và \(Ox'\) là hai tia đối nhau) nên \(\widehat {xOy'} + \widehat {y'Ox'} = 180^\circ \),

suy ra \(\widehat {xOy'} = 180^\circ  - \widehat {y'Ox'} = 180^\circ  - 120^\circ  = 60^\circ \).

Bài 8: Hai đường thẳng MN và PQ cắt nhau tại A tạo thành MAP có số đo bằng \(30^\circ \).

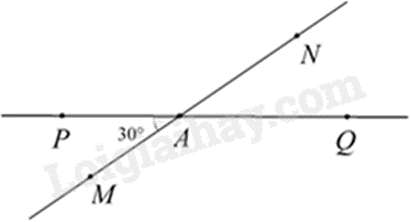
a) Tính số đo góc NAQ.

b) Tính số đo góc MAQ.

c) Viết tên các cặp góc đối đỉnh.

d) Viết tên các cặp góc kề bù.

Phương pháp

Sử dụng khái niệm hai góc kề bù, đối đỉnh và tính chất:

- Hai góc đối đỉnh thì bằng nhau.

- Hai góc kề bù thì có tổng bằng \(180^\circ \).

Lời giải

a) Vì \(\widehat {MAP}\) và \(\widehat {NAQ}\) là hai góc đối đỉnh nên \(\widehat {MAP} = \widehat {NAQ} = 30^\circ \).

b) Vì \(\widehat {MAQ}\) kề bù với \(\widehat {MAP}\) nên \(\widehat {MAQ} = 180^\circ  - \widehat {MAP} = 180^\circ  - 30^\circ  = 150^\circ \).

c) Các cặp góc đối đỉnh là: \(\widehat {MAP}\) và \(\widehat {NAQ}\); \(\widehat {MAQ}\) và \(\widehat {PAN}\).

d) Các cặp góc bù nhau là: \(\widehat {MAP}\) và \(\widehat {MAQ}\); \(\widehat {MAP}\) và \(\widehat {PAN}\); \(\widehat {NAQ}\) và \(\widehat {MAQ}\); \(\widehat {NAQ}\) và \(\widehat {PAN}\).

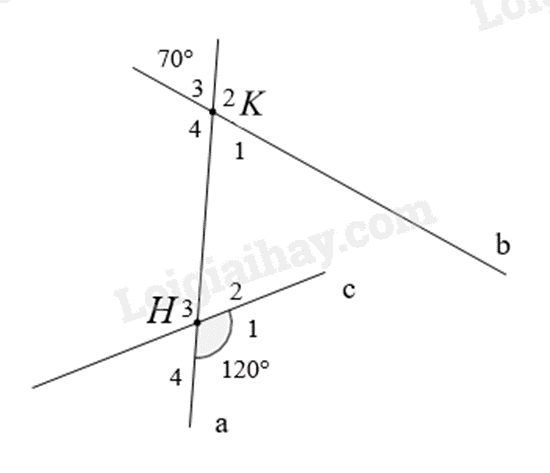
Bài 9: Tính số đo các góc còn lại trong hình vẽ sau:

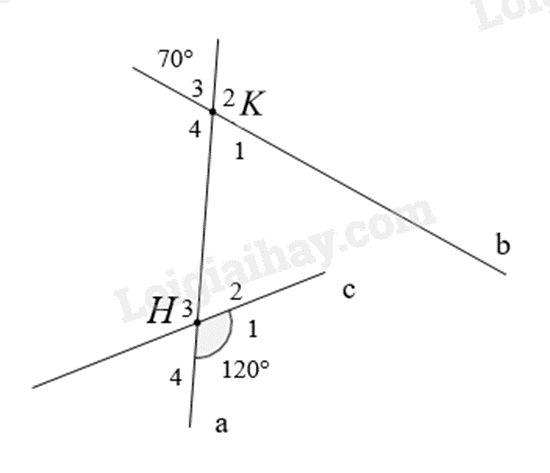
Phương pháp

- Hai góc đối đỉnh thì bằng nhau.

- Hai góc kề bù thì có tổng số đo góc bằng \(180^\circ \).

Lời giải

* Vì \(\widehat {{K_2}} + \widehat {{K_3}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{K_2}} = 180^\circ  - \widehat {{K_3}} = 180^\circ  - 70^\circ  = 110^\circ \).

Ta có: \(\widehat {{K_1}} = \widehat {{K_3}} = 70^\circ \) (hai góc đối đỉnh); \(\widehat {{K_4}} = \widehat {{K_2}} = 110^\circ \) (hai góc đối đỉnh).

* Vì \(\widehat {{H_1}} + \widehat {{H_2}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{H_2}} = 180^\circ  - \widehat {{H_1}} = 180^\circ  - 120^\circ  = 60^\circ \).

Ta có: \(\widehat {{H_3}} = \widehat {{H_1}} = 120^\circ \) (hai góc đối đỉnh); \(\widehat {{H_4}} = \widehat {{H_2}} = 60^\circ \).

Bài 10: Cho hình vẽ:

a) Kể tên các cặp góc so le trong, các cặp góc đồng vị.

b) Tính \(\widehat {{M_4}} + \widehat {{N_3}};\widehat {{M_3}} + \widehat {{N_1}}\).

Phương pháp

a) Dựa vào kiến thức về góc tạo bởi một đường thẳng với hai cắt hai đường thẳng.

b) Tính các góc còn lại dựa vào kiến thức về hai góc đối đỉnh, kề bù.

Lời giải

a) Các cặp góc so le trong là: \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\), \(\widehat {{M_3}}\) và \(\widehat {{N_1}}\).

Các cặp góc đồng vị là: \(\widehat {{M_1}}\) và \(\widehat {{N_1}}\), \(\widehat {{M_2}}\) và \(\widehat {{N_2}}\), \(\widehat {{M_3}}\) và \(\widehat {{N_3}}\), \(\widehat {{M_4}}\) và \(\widehat {{N_4}}\).

b) +) Vì \(\widehat {{N_3}} + \widehat {{N_2}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{N_3}} = 180^\circ  - \widehat {{N_2}} = 180^\circ  - 50^\circ  = 130^\circ \)

Do đó \(\widehat {{M_4}} + \widehat {{N_3}} = 50^\circ  + 130^\circ  = 180^\circ \).

+) Vì \(\widehat {{M_3}} + \widehat {{M_4}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{M_3}} = 180^\circ  - \widehat {{M_4}} = 180^\circ  - 50^\circ  = 130^\circ \)

Ta có: \(\widehat {{N_1}} = \widehat {{N_3}} = 130^\circ \) (hai góc đối đỉnh) nên \(\widehat {{M_3}} + \widehat {{N_1}} = 130^\circ  + 130^\circ  = 260^\circ \).