TUYENSINH247 KHAI GIẢNG KHOÁ HỌC LỚP 1-9 NĂM MỚI 2025-2026

GIẢM 35% HỌC PHÍ + TẶNG KÈM SỔ TAY KIẾN THỨC ĐỘC QUYỀN

Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học

Bài 2. Tỉ số lượng giác của góc nhọn

Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 1 - Hình học 9

Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 1 - Hình học 9

Đề bài

Bài 1. Cho $∆ABC$ vuông tại A và $\widehat B = \alpha .$ Chứng minh rằng:

a. ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$

b. $\tan \alpha = {{\sin \alpha } \over {\cos \alpha }}$

Bài 2. Hãy sắp xếp các tỉ số lượng giác sau đây theo thứ tự tăng dần (không dùng bảng số và máy tính) :

a. $\sin 40^\circ ,\,\cos 28^\circ ,\,\sin 65^\circ ,\,\cos 88^\circ$

b. $\tan 65^\circ ,\cot 42^\circ ,\tan 76^\circ ,\cot 27^\circ .$

Phương pháp giải - Xem chi tiết

1. Sử dụng:

$\sin \alpha = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}};\cos \alpha = \dfrac{{cạnh\,kề}}{{cạnh\,huyền}}$

2. Sử dụng:

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Nếu $\alpha<\beta$ thì $\sin \alpha<\sin \beta;$ $\tan \alpha<\tan \beta$

Lời giải chi tiết

Bài 1.

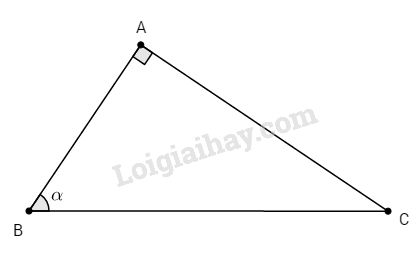
a. Đặt $AB=c,AC=b,BC=a$

Vì tam giác ABC vuông tại A nên theo định lý Pytago ta có: $a^2=b^2+c^2$

Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: $\sin \alpha = {b \over a} \Rightarrow {\sin ^2}\alpha = {{{b^2}} \over {{a^2}}}$

$\cos \alpha = {c \over a} \Rightarrow {\cos ^2}\alpha = {{{c^2}} \over {{a^2}}}$

Do đó: ${\sin ^2}\alpha + {\cos ^2}\alpha = {{{b^2} + {c^2}} \over {{a^2}}} = {{{a^2}} \over {{a^2}}} = 1$

b. $\tan \alpha = {b \over c} = {b \over c}:{c \over a} = {{\sin \alpha } \over {\cos \alpha }}$

Bài 2. a. Ta có:

$\eqalign{ & \cos 28^\circ = \sin \left( {90^\circ - 28^\circ } \right) = \sin 62^\circ \cr & \cos 88^\circ = \sin \left( {90^\circ - 88^\circ } \right) = \sin 2^\circ \cr}$

Mà $\sin 2^\circ < \sin 40^\circ < \sin 62^\circ < \sin 65^\circ$ (góc tăng thì sin tăng)

$\Rightarrow \cos 88^\circ < \sin 40^\circ < \cos 28^\circ$ $\, < \sin 65^\circ .$

b. Ta có:

$\eqalign{ & \cot 42^\circ = \tan \left( {90^\circ - 42^\circ } \right) = \tan 48^\circ \cr & \cot 27^\circ = \tan \left( {90^\circ - 27^\circ } \right) = \tan 63^\circ \cr}$

Mà $\tan 48^\circ < \tan 63^\circ < \tan 65^\circ < \tan 76^\circ$

$\Rightarrow \cot 42^\circ < \cot 27^\circ < \tan 65^\circ$ $\, < \tan 76^\circ$

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 9
Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 9
Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 9
Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 1 - Hình học 9
Bài 17 trang 77 SGK Toán 9 tập 1
Tìm giá trị của x trong hình 23:
Bài 16 trang 77 SGK Toán 9 tập 1
Cho tam giác vuông có một góc, cạnh huyền...
Bài 15 trang 77 SGK Toán 9 tập 1
Cho tam giác ABC vuông tại A, hãy tính các tỷ số lượng giác của góc C
Bài 14 trang 77 SGK Toán 9 tập 1
Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh...
Bài 13 trang 77 SGK Toán 9 tập 1
Giải bài 13 trang 77 SGK Toán 9 tập 1. Dựng góc α biết:
Bài 12 trang 76 SGK Toán 9 tập 1
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ...
Bài 11 trang 76 SGK Toán 9 tập 1
Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.
Bài 10 trang 76 SGK Toán 9 tập 1
Vẽ một tam giác vuông...
Trả lời câu hỏi 4 Bài 2 trang 74 SGK Toán 9 Tập 1
Trả lời câu hỏi 4 Bài 2 trang 74 SGK Toán 9 Tập 1. Cho hình 19, hãy cho biết tổng số đo...
Trả lời câu hỏi 3 Bài 2 trang 74 SGK Toán 9 Tập 1
Giải Trả lời câu hỏi Bài 2 trang 74 SGK Toán 9 Tập 1. Hãy nêu cách dựng góc nhọn
Trả lời câu hỏi 2 Bài 2 trang 73 SGK Toán 9 Tập 1
Cho tam giác ABC vuông tại A có
Trả lời câu hỏi 1 Bài 2 trang 71 SGK Toán 9 Tập 1
Xét tam giác ABC vuông tại A
Lý thuyết về tỷ số lượng giác của góc nhọn
Lý thuyết về tỷ số lượng giác của góc nhọn

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE

Bài giải mới nhất