Bài 8 trang 105 SGK Toán 11 tập 2 - Kết nối tri thức
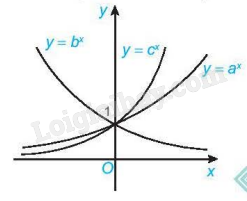
Cho đồ thị ba hàm số mũ (y = {a^x},y = {b^x}) và (y = {c^x}) như trong hình vẽ dưới đây
Đề bài
Cho đồ thị ba hàm số mũ \(y = {a^x},y = {b^x}\) và \(y = {c^x}\) như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
A. \(a > c > b\).
B. \(b > a > c\).
C. \(c > a > b\).
D. \(c > b > a\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đồ thị hàm số \(y = {a^x}\) đồng biến nếu \(a > 1\)
Đồ thị hàm số \(y = {a^x}\) nghịch biến nếu \(0 < a < 1\)
Lời giải chi tiết
Đồ thị hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\)
Đồ thị hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1\)
Với \(x > 0\) bất kì ta có \({c^x} > {a^x} \Leftrightarrow c > a\)
Đáp án C
- Bài 9 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 10 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức













Danh sách bình luận