-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Góc và đường thẳng song song
-
Chương 4: Tam giác bằng nhau
-
Chương 5: Thu thập và biểu diễn dữ liệu
-
Chương 6: Tỉ lệ thức và đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số và đa thức một biến
-
Chương 8: Làm quen với biến cố và xác suất
-
Chương 9: Quan hệ giữa các yếu tố trong một tam giác
- Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 32: Quan hệ đường vuông góc và đường xiên
- Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
-
Chương 10: Một số hình khối trong thực tiễn
Trắc nghiệm Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết Toán 7 Kết nối tri thức
Đề bài
Điền vào chỗ trống:
“Nếu hai đường thẳng a và b cắt đường thẳng c tạo thành một cặp góc đồng vị … thì các cặp góc so le trong bằng nhau”
-
A.
bù nhau
-
B.
bằng nhau
-
C.
phụ nhau
-
D.
kề nhau
-
A.
\(\widehat {{A_2}} = \widehat {{B_4}}\)
-
B.
\(\widehat {{A_3}} = \widehat {{B_2}}\)
-
C.
\(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \)
-
D.
\(\widehat {{B_2}} = \widehat {{B_4}}\)
-
A.
\(a \bot b\)
-
B.
\(\widehat {{A_2}} = 60^\circ \)
-
C.
\(\widehat {{B_2}} = 120^\circ \)
-
D.
\(a//b\)
-
A.
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B.
\(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C.
\(\widehat {DCA}\) và \(\widehat {AFE}\) là hai góc so le trong
-
D.
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
-
A.
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
-
A.
\(\widehat {AEF} = 125^\circ \)
-
B.
\(AB//C{\rm{D}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Vẽ \(\Delta ABC\). Qua A vẽ đường thẳng d1 vuông góc với AB; đường thẳng d2 đi qua C và vuông góc với d1. Phát biểu nào sau đây là đúng?
-
A.
d1\( \bot \)AC
-
B.
AB // d2
-
C.
d1 // AC
-
D.
d1 \( \bot \)BC
-
A.
.\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B.
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C.
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D.
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({135^0}\)
-
D.
\({145^0}\)
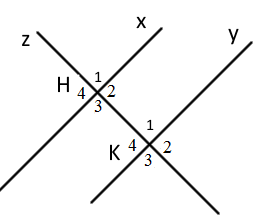
Cho hình vẽ sau:
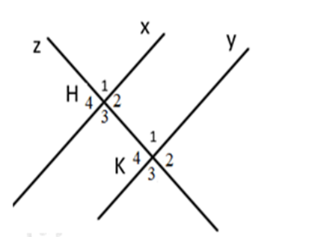
Chọn phát biểu đúng.
-
A.
\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B.
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C.
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D.
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong.
Chọn một cặp góc đồng vị trong hình vẽ sau:
-
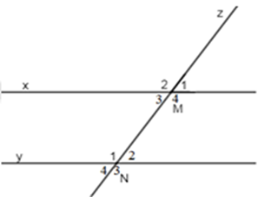
A.
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Chọn một cặp góc so le trong trong hình vẽ sau:
-
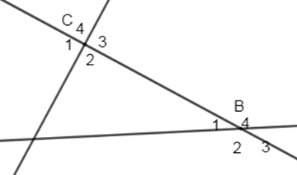
A.
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\)
-
B.
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\)
-
C.
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\)
-
D.
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\)
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
-
A.
Hai góc trong cùng phía bằng nhau
-
B.
Hai góc đồng vị bằng nhau
-
C.
Hai góc so le trong còn lại có tổng bằng \({120^0}\)
-
D.
Tất cả các đáp án trên đều đúng
Cho hình vẽ sau:
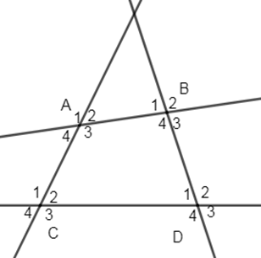
Có bao nhiêu cặp góc đồng vị?
-
A.
$4$
-
B.
$12$
-
C.
$8$
-
D.
$16$
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
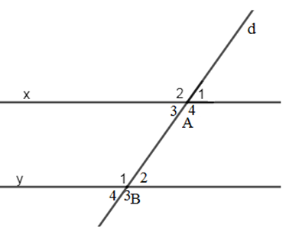
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({135^0}\)
-
D.
\({145^0}\)
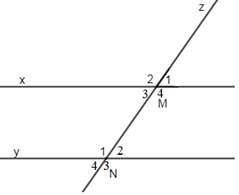
Cho hình vẽ sau:
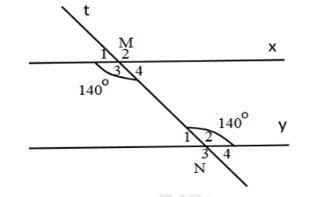
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({180^0}\)
-
D.
\({145^0}\)
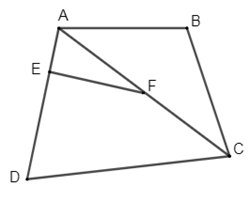
Cho hình vẽ sau:
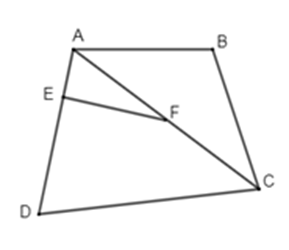
Em hãy chọn câu đúng nhất trong các câu sau:
-
A.
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B.
$\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C.
\(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong
-
D.
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Tính giá trị \(x;y;z;t\) trên hình sau:
-
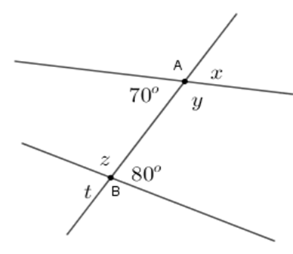
A.
$x = {80^o};y = {110^0};z = {100^o};t = {70^o}$
-
B.
$x = {70^o};y = {100^0};z = {110^o};t = {80^o}$
-
C.
$x = {70^o};y = {110^0};z = {100^o};t = {80^o}$ \(\)
-
D.
$x = {70^o};y = {100^0};z = {100^o};t = {80^o}$
Cho hình vẽ sau:
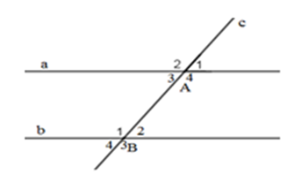
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
-
A.
\(\widehat {{A_4}} = \widehat {{B_1}} = {150^0}\)
-
B.
\(\widehat {{A_4}} = \widehat {{B_1}} = {120^0}\)
-
C.
\(\widehat {{A_4}} = {120^o};\widehat {{B_1}} = {150^0}\) \(\)
-
D.
\(\widehat {{A_4}} = \widehat {{B_1}} = {100^0}\)
Chọn câu trả lời đúng trong các câu sau: Trong mặt phẳng,
-
A.
Hai đường thẳng không có điểm chung thì song song với nhau.
-
B.
Hai đoạn thẳng có điểm chung thì song song với nhau.
-
C.
Hai đường thẳng có hai điểm chung thì song song với nhau.
-
D.
Hai đường thẳng song song là hai đường thẳng không trùng nhau.
Chọn câu đúng nhất.
-
A.
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì $a//b.$
-
B.
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì $a//b.$
-
C.
Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
-
D.
Cả A, B, C đều đúng.
Cho hình vẽ dưới đây :
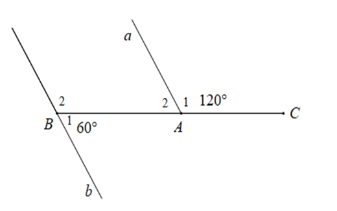
Chọn câu sai.
-
A.
\(a \bot b\)
-
B.
\(\widehat {{A_2}} = 60^\circ \)
-
C.
\(\widehat {{B_2}} = 120^\circ \)
-
D.
\(a//b\)
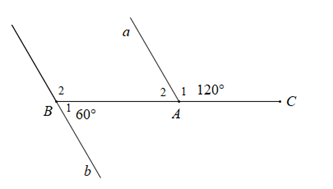
Cho hình vẽ:
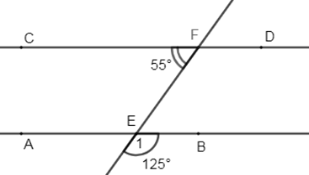
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
-
A.
\(\widehat {AEF} = 125^\circ \)
-
B.
\(AB//C{\rm{D}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Lời giải và đáp án
Điền vào chỗ trống:
“Nếu hai đường thẳng a và b cắt đường thẳng c tạo thành một cặp góc đồng vị … thì các cặp góc so le trong bằng nhau”
-
A.
bù nhau
-
B.
bằng nhau
-
C.
phụ nhau
-
D.
kề nhau
Đáp án : B
Dựa vào tính chất các góc tạo bởi một đường thẳng cắt 2 đường thẳng.
Nếu hai đường thẳng a và b cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
-
A.
\(\widehat {{A_2}} = \widehat {{B_4}}\)
-
B.
\(\widehat {{A_3}} = \widehat {{B_2}}\)
-
C.
\(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \)
-
D.
\(\widehat {{B_2}} = \widehat {{B_4}}\)
Đáp án : B
Dựa vào tính chất các góc tạo bởi một đường thẳng cắt 2 đường thẳng.
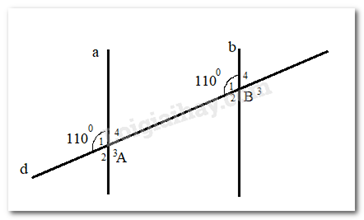
Vì đường thẳng d cắt 2 đường thẳng a và b tạo thành cặp góc A1 và B1 bằng nhau ( cùng bằng 110\(^\circ \)) nên:
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) (2 góc đồng vị)
Mà \(\widehat {{B_2}} = \widehat {{B_4}}\) (2 góc đối đỉnh)
Suy ra \( \widehat {{A_2}} = \widehat {{B_4}}\) nên A đúng
+) \(\widehat {{A_3}} = \widehat {{B_3}}\) (2 góc đồng vị)
Mà \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) (2 góc kề bù) và \(\widehat {{A_1}} = \widehat {{A_3}}\); \(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh) nên \(\widehat {{B_2}} + 110^\circ = 180^\circ \)
Suy ra \( \widehat {{B_2}} = 70^\circ \)
Ta thấy \( \widehat {{A_3}} \ne \widehat {{B_2}}\) nên B sai
+) \(\widehat {{A_1}} = \widehat {{B_1}}\)(=110\(^\circ \))
Mà \(\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \) (2 góc kề bù)
Suy ra \(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \) nên C đúng
Ta có: \(\widehat {{B_2}} = \widehat {{B_4}}\) (2 góc đối đỉnh) nên D đúng
-
A.
\(a \bot b\)
-
B.
\(\widehat {{A_2}} = 60^\circ \)
-
C.
\(\widehat {{B_2}} = 120^\circ \)
-
D.
\(a//b\)
Đáp án : A
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy khẳng định A sai
-
A.
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B.
\(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C.
\(\widehat {DCA}\) và \(\widehat {AFE}\) là hai góc so le trong
-
D.
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Đáp án : A
Áp dụng khái niệm hai góc đồng vị, so le trong
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- \(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) nên B sai
- \(\widehat {DCA}\) và \(\widehat {AFE}\) là hai góc so le trong (sai, vì đó là hai góc đồng vị) nên C sai
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) nên D sai
-
A.
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Đáp án : D
Áp dụng khái niệm hai góc đồng vị, so le trong, so le ngoài, trong cùng phía
- \(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
- \(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
- \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
- \(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
-
A.
\(\widehat {AEF} = 125^\circ \)
-
B.
\(AB//C{\rm{D}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Đáp án : C
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b,\) trong các góc tạo thành có \(1\) cặp góc so le trong bằng nhau thì \(a//b\).
Ta có:\(\widehat{AEF} = \widehat {{E_1}}\) ( 2 góc đối đỉnh) nên \(\widehat{AEF} = 125^0\)
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} = {180^0} - {125^0} = {55^0} \Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) ở vị trí so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Vẽ \(\Delta ABC\). Qua A vẽ đường thẳng d1 vuông góc với AB; đường thẳng d2 đi qua C và vuông góc với d1. Phát biểu nào sau đây là đúng?
-
A.
d1\( \bot \)AC
-
B.
AB // d2
-
C.
d1 // AC
-
D.
d1 \( \bot \)BC
Đáp án : B
Vẽ hình và chứng minh sự vuông góc hay song song của d1 , d2 với các đường thẳng khác.
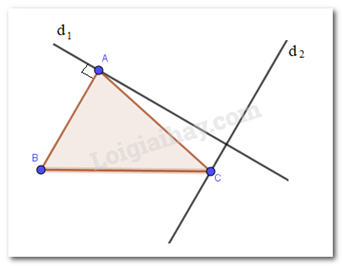
Vì AB và d2 cùng vuông góc với d1 nên AB // d2
-
A.
.\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B.
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C.
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D.
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong
Đáp án : B
Áp dụng khái niệm hai góc đồng vị, so le trong, so le ngoài, trong cùng phía.
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({135^0}\)
-
D.
\({145^0}\)
Đáp án : D
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1 cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\) nên cặp góc so le trong còn lại cũng bằng nhau
\( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
Chọn phát biểu đúng.
-
A.
\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B.
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C.
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D.
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong.
Đáp án : B
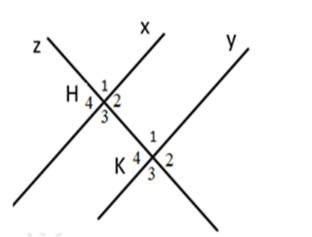
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Chọn một cặp góc đồng vị trong hình vẽ sau:
-
A.
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Đáp án : D
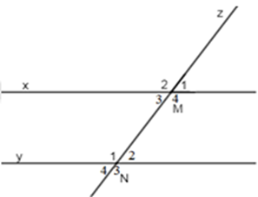
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
Chọn một cặp góc so le trong trong hình vẽ sau:
-
A.
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\)
-
B.
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\)
-
C.
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\)
-
D.
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\)
Đáp án : A
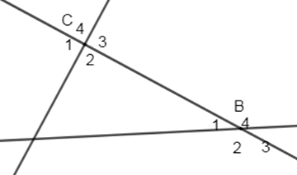
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (đúng) chọn A
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại B
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại C
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc trong cùng phía), loại D.
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
-
A.
Hai góc trong cùng phía bằng nhau
-
B.
Hai góc đồng vị bằng nhau
-
C.
Hai góc so le trong còn lại có tổng bằng \({120^0}\)
-
D.
Tất cả các đáp án trên đều đúng
Đáp án : B
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Nếu đường thẳng $c$ cắt hai đường thẳng $a,b$ và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: hai góc đồng vị bằng nhau
Cho hình vẽ sau:
Có bao nhiêu cặp góc đồng vị?
-
A.
$4$
-
B.
$12$
-
C.
$8$
-
D.
$16$
Đáp án : D
Các cặp góc đồng vị là: \(\widehat {{A_1}}\) và \(\widehat {{C_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{C_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{C_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{C_3}}\), \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{B_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{B_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{B_4}}\) và \(\widehat {{D_4}}\).
Tương tự ta có thêm $8$ cặp góc đồng vị \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{B_3}}\), \(\widehat {{C_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{C_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{C_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{C_4}}\) và \(\widehat {{D_4}}\).
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({135^0}\)
-
D.
\({145^0}\)
Đáp án : D
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.
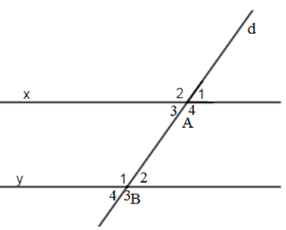
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1
cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\)nên \( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({180^0}\)
-
D.
\({145^0}\)
Đáp án : C
Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\).
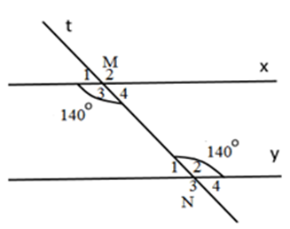
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\end{array}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\end{array}\)
Cho hình vẽ sau:
Em hãy chọn câu đúng nhất trong các câu sau:
-
A.
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B.
$\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C.
\(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong
-
D.
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Đáp án : A
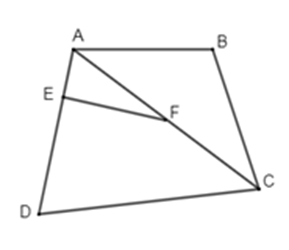
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- $\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) loại B
- \(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong (sai, vì đó là hai góc đồng vị) loại C
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) loại D
Tính giá trị \(x;y;z;t\) trên hình sau:
-
A.
$x = {80^o};y = {110^0};z = {100^o};t = {70^o}$
-
B.
$x = {70^o};y = {100^0};z = {110^o};t = {80^o}$
-
C.
$x = {70^o};y = {110^0};z = {100^o};t = {80^o}$ \(\)
-
D.
$x = {70^o};y = {100^0};z = {100^o};t = {80^o}$
Đáp án : C
Sử dụng tổng hai góc kề bù bằng \({180^o}\) , tính chất hai góc đối đỉnh
Ta có \(x = {70^0}\) (tính chất hai góc đối đỉnh)
\(y + {70^o} = {180^o} \Rightarrow y = {110^o}\) (hai góc kề bù)
Tương tự ta có \(t = {80^o};\,z = {100^o}\)
Vậy $x = {70^o};y = {110^0};z = {100^o};t = {80^o}.$
Cho hình vẽ sau:
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
-
A.
\(\widehat {{A_4}} = \widehat {{B_1}} = {150^0}\)
-
B.
\(\widehat {{A_4}} = \widehat {{B_1}} = {120^0}\)
-
C.
\(\widehat {{A_4}} = {120^o};\widehat {{B_1}} = {150^0}\) \(\)
-
D.
\(\widehat {{A_4}} = \widehat {{B_1}} = {100^0}\)
Đáp án : A
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)
Chọn câu trả lời đúng trong các câu sau: Trong mặt phẳng,
-
A.
Hai đường thẳng không có điểm chung thì song song với nhau.
-
B.
Hai đoạn thẳng có điểm chung thì song song với nhau.
-
C.
Hai đường thẳng có hai điểm chung thì song song với nhau.
-
D.
Hai đường thẳng song song là hai đường thẳng không trùng nhau.
Đáp án : A
Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn câu đúng nhất.
-
A.
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì $a//b.$
-
B.
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì $a//b.$
-
C.
Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
-
D.
Cả A, B, C đều đúng.
Đáp án : D
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
nên cả A, B, C đều đúng.
Cho hình vẽ dưới đây :
Chọn câu sai.
-
A.
\(a \bot b\)
-
B.
\(\widehat {{A_2}} = 60^\circ \)
-
C.
\(\widehat {{B_2}} = 120^\circ \)
-
D.
\(a//b\)
Đáp án : A
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy A sai.
Cho hình vẽ:
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
-
A.
\(\widehat {AEF} = 125^\circ \)
-
B.
\(AB//C{\rm{D}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Đáp án : C
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng $c$ cắt hai đường thẳng $a$ và $b,$ trong các góc tạo thành có $1$ cặp góc so le trong bằng nhau thì \(a//b\).
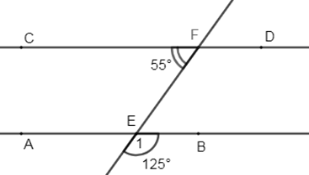
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù (gt)
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \)\(\Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} \)\(= {180^0} - {125^0} = {55^0} \)\(\Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Lại có \(\widehat {{E_1}}=\widehat {{AEF}}\) (hai góc đối đỉnh) nên \(\widehat {{AEF}}=125^0\)
Vậy cả A, B đều đúng.
Luyện tập và củng cố kiến thức Bài 10: Tiên đề Euclid. Tính chất của các đường thẳng song song Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 11: Định lí và chứng minh định lí Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 36: Hình hộp chữ nhật và hình lập phương Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 33: Quan hệ giữa ba cạnh trong một tam giác Toán 7 Kết nối tri thức
