-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Góc và đường thẳng song song
-
Chương 4: Tam giác bằng nhau
-
Chương 5: Thu thập và biểu diễn dữ liệu
-
Chương 6: Tỉ lệ thức và đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số và đa thức một biến
-
Chương 8: Làm quen với biến cố và xác suất
-
Chương 9: Quan hệ giữa các yếu tố trong một tam giác
- Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 32: Quan hệ đường vuông góc và đường xiên
- Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
-
Chương 10: Một số hình khối trong thực tiễn
Trắc nghiệm Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ Toán 7 Kết nối tri thức
Đề bài
Tính: \({\left( {\frac{{ - 3}}{7}} \right)^3}\)
-
A.
\(\frac{{ - 9}}{{21}}\)
-
B.
\(\frac{{27}}{{343}}\)
-
C.
-\(\frac{{27}}{{343}}\)
-
D.
\(\frac{{ - 7}}{9}\)
Tính 94 . 35
-
A.
39
-
B.
311
-
C.
279
-
D.
313
-
A.
\(\frac{1}{{18}}\)
-
B.
-1152
-
C.
1152
-
D.
96
Chọn khẳng định đúng:
-
A.
(-4)3 . 45 = (-4)8
-
B.
am : bn = am-n
-
C.
(-6)2021 = 62021
-
D.
[(-3)2]5 = 310
Tìm x, biết: 27x . 34 = 95
-
A.
2
-
B.
3
-
C.
1
-
D.
4
Tính A = 1 + 3 + 32 +…+ 32022
-
A.
\(\frac{{{3^{2023}} + 1}}{2}\)
-
B.
\({3^{2023}}\)
-
C.
\({3^{2023}} - 1\)
-
D.
\(\frac{{{3^{2023}} - 1}}{2}\)
Biết khối lượng của Mặt Trời là khoảng 1 988 550 . 1021 tấn, khối lượng của Trái Đất khoảng 0,6 . 1022 tấn. Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng Trái Đất?
-
A.
3314250
-
B.
331425
-
C.
3. 10-6
-
D.
33142,5
Tìm x biết: (2x+1)3 – 1 = -344
-
A.
x = 7
-
B.
x = -7
-
C.
x = 3
-
D.
x = -4
Tính giá trị biểu thức \(M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\) tại x = 3
-
A.
-54
-
B.
\(\frac{{ - 1}}{{54}}\)
-
C.
\(\frac{7}{{108}}\)
-
D.
\( - \frac{2}{9}\)
Chọn câu sai. Với hai số hữu tỉ \(a,\,b\) và các số tự nhiên \(m,\,n\) ta có
-
A.
${a^m}.{a^n} = {a^{m + n}}$
-
B.
${\left( {a.b} \right)^m} = {a^m}.{b^m}$
-
C.
\({\left( {{a^m}} \right)^n} = {a^{m + n}}\)
-
D.
${\left( {{a^m}} \right)^n} = {a^{m.n}}$
Tính \({\left( {\dfrac{2}{3}} \right)^3}\)
-
A.
$\dfrac{8}{9}$
-
B.
$\dfrac{8}{{27}}$
-
C.
\(\dfrac{4}{9}\)
-
D.
$\dfrac{4}{{27}}$
Chọn khẳng định đúng. Với số hữu tỉ \(x\) ta có
-
A.
${x^0} = x$
-
B.
${x^1} = 1$
-
C.
\({x^0} = 0\)
-
D.
${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$
Kết quả của phép tính \({\left( {\dfrac{1}{7}} \right)^2}{.7^2}\) là:
-
A.
$7$
-
B.
$\dfrac{1}{{49}}$
-
C.
\(\dfrac{1}{7}\)
-
D.
$1$
Chọn câu sai.
-
A.
${\left( {-2019} \right)^0} = 1$
-
B.
$\left( {0,5} \right).{\left( {0,5} \right)^2} = \dfrac{1}{4}$
-
C.
${4^6}:{\rm{ }}{4^4} = 16$
-
D.
${\left( {-3} \right)^3}.{\left( {-{\rm{ }}3} \right)^{{\rm{ }}2}} = {\left( { - 3} \right)^5}$
Số ${x^{12}}$ (với $x \ne 0$) không bằng số nào trong các số sau đây ?
-
A.
${x^{18}}:{x^6}(x\; \ne 0)$
-
B.
${x^4}.{\rm{ }}{x^8}$
-
C.
${x^2}.{\rm{ }}{x^6}$
-
D.
${\left( {{x^3}} \right)^4}$
Số ${2^{24}}$ viết dưới dạng lũy thừa có số mũ $8$ là:
-
A.
${8^8}$
-
B.
${9^8}$
-
C.
${6^8}$
-
D.
Một đáp số khác
Số $x$ sao cho ${2^x}\; = {\left( {{2^2}} \right)^5}$ là :
-
A.
\(5\)
-
B.
$7$
-
C.
${2^7}$
-
D.
$10$
Số $a$ thỏa mãn $a:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$ là :
-
A.
$\dfrac{1}{3}$
-
B.
${\left( {\dfrac{1}{3}} \right)^7}$
-
C.
${\left( {\dfrac{1}{3}} \right)^6}$
-
D.
$\dfrac{1}{{18}}$
Giá trị nhỏ nhất của biểu thức ${\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}}$ đạt được là:
-
A.
$ - \dfrac{1}{2}$
-
B.
$\dfrac{{ - 1}}{{100}}$
-
C.
$\dfrac{1}{{100}}$
-
D.
$\dfrac{{81}}{{100}}$
Cho ${20^n}\;:\;{5^n} = 4$ thì :
-
A.
$n = 0$
-
B.
$n = 3$
-
C.
$n = 2$
-
D.
$n = 1$
Cho biểu thức $A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}}$. Chọn khẳng định đúng.
-
A.
$A > 1$
-
B.
$A < 1$
-
C.
$A > 2$
-
D.
$A = 1$
Giá trị của biểu thức \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}}\) là
-
A.
$\dfrac{4}{5}$
-
B.
$\dfrac{5}{4}$
-
C.
$\dfrac{{22}}{{30}}$
-
D.
$\dfrac{{15}}{{11}}$
Tìm \(x\), biết \({\left( {5x - 1} \right)^6} = 729\)
-
A.
\(x = \dfrac{4}{5}\); \(x = \dfrac{2}{5}\)
-
B.
\(x = - \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
-
C.
\(x = \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
-
D.
\(x = - \dfrac{4}{5}\); \(x = \dfrac{2}{5}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = - 0,001\)?
-
A.
$0$
-
B.
$1$
-
C.
$2$
-
D.
$3$
Tìm số tự nhiên \(n\) thỏa mãn \({5^n} + {5^{n + 2}} = 650\).
-
A.
$n = 1$
-
B.
$n = 2$
-
C.
$n = 3$
-
D.
$n = 4$
Cho biết : \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\) . Tính nhanh giá trị của biểu thức sau:
\(S = \left( {{{12}^2} + {{14}^2} + {{16}^2} + {{18}^2} + {{20}^2}} \right) - \left( {{1^2} + {3^2} + {5^2} + {7^2} + {9^2}} \right)\)
-
A.
$1155$
-
B.
$5511$
-
C.
$5151$
-
D.
$1515$
Cho \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\). Chọn đáp án đúng.
-
A.
\(A\) không phải là một số nguyên
-
B.
\(A\) là một số nguyên
-
C.
\(A\) là một số nguyên dương
-
D.
\(A\) là một số nguyên âm
Lời giải và đáp án
Tính: \({\left( {\frac{{ - 3}}{7}} \right)^3}\)
-
A.
\(\frac{{ - 9}}{{21}}\)
-
B.
\(\frac{{27}}{{343}}\)
-
C.
-\(\frac{{27}}{{343}}\)
-
D.
\(\frac{{ - 7}}{9}\)
Đáp án : C
Sử dụng định nghĩa lũy thừa của một số hữu tỉ:
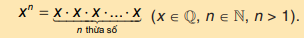
\({\left( {\frac{{ - 3}}{7}} \right)^3} = \left( {\frac{{ - 3}}{7}} \right).\left( {\frac{{ - 3}}{7}} \right).\left( {\frac{{ - 3}}{7}} \right) = \frac{{( - 3).( - 3).( - 3)}}{{7.7.7}} = \frac{{ - 27}}{{343}}\)
Tính 94 . 35
-
A.
39
-
B.
311
-
C.
279
-
D.
313
Đáp án : D
Bước 1: Đưa 2 lũy thừa về dạng 2 lũy thừa có cùng cơ số
Bước 2: Sử dụng công thức nhân 2 lũy thừa cùng cơ số: am . an = am+n
Chú ý: (ap)q = ap.q
Ta có: 94 . 35 = (32)4 . 35 = 32.4 . 35 = 38 . 35 = 38+5 = 313
-
A.
\(\frac{1}{{18}}\)
-
B.
-1152
-
C.
1152
-
D.
96
Đáp án : C
Bước 1: Tính lũy thừa
Bước 2: Chia 2 số hữu tỉ
\(8:{\left( {\frac{2}{3} - \frac{3}{4}} \right)^2} = 8:{\left( {\frac{8}{{12}} - \frac{9}{{12}}} \right)^2} = 8:{\left( {\frac{{ - 1}}{{12}}} \right)^2} = 8:\frac{1}{{144}} = 8.144 = 1152\)
Chọn khẳng định đúng:
-
A.
(-4)3 . 45 = (-4)8
-
B.
am : bn = am-n
-
C.
(-6)2021 = 62021
-
D.
[(-3)2]5 = 310
Đáp án : D
Sử dụng các công thức:
xm : xn = xm-n (\(x \ne 0;m \ge n\))
xm . xn = xm+n
(xm)n = xm.n
(-x)m = xm ( với m chẵn)
(-x)m = - xm ( với m lẻ)
+) (-4)3 . 45 = - 43 . 45 = - 43+5 = - 48
Vậy A sai
+) am : an = am-n thiếu điều kiện \(a \ne 0; m \ge n\)
Vậy B sai
+) (-6)2021 = - 62021 ( vì 2021 là số lẻ)
Vậy C sai
+) [(-3)2]5 = (32)5 = 32.5 = 310
Vậy D đúng
Tìm x, biết: 27x . 34 = 95
-
A.
2
-
B.
3
-
C.
1
-
D.
4
Đáp án : A
Đưa các lũy thừa về dạng các lũy thừa có cùng cơ số
Với a \( \ne \)0; a \( \ne \) 1 thì am = an khi m = n
27x . 34 = 95
\( \Rightarrow \) (33)x . 34 = (32)5
\( \Rightarrow \)33.x . 34 = 310
\( \Rightarrow \)33x = 310 : 34
\( \Rightarrow \)33x = 36
\( \Rightarrow \)3x = 6
\( \Rightarrow \)x = 2
Vậy x = 2
Tính A = 1 + 3 + 32 +…+ 32022
-
A.
\(\frac{{{3^{2023}} + 1}}{2}\)
-
B.
\({3^{2023}}\)
-
C.
\({3^{2023}} - 1\)
-
D.
\(\frac{{{3^{2023}} - 1}}{2}\)
Đáp án : D
Phát hiện quy luật của tổng
Bước 1: Tìm 3.A
Bước 2: Thực hiện tính 3A – A
Bước 3: Tính A
Ta có: A = 1 + 3 + 32 +…+ 32022
\( \Rightarrow \)3.A = 3. ( 1 + 3 + 32 +…+ 32022) = 3 + 32 + 33 +…+ 32023
\( \Rightarrow \) 3. A – A = 3 + 32 + 33 +…+ 32023 – (1 + 3 + 32 +…+ 32022)
2A = 3 + 32 + 33 +…+ 32023 – 1 - 3 - 32 - …- 32022 = 32023 – 1
\( \Rightarrow A = \frac{{{3^{2023}} - 1}}{2}\)
Biết khối lượng của Mặt Trời là khoảng 1 988 550 . 1021 tấn, khối lượng của Trái Đất khoảng 0,6 . 1022 tấn. Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng Trái Đất?
-
A.
3314250
-
B.
331425
-
C.
3. 10-6
-
D.
33142,5
Đáp án : B
Tính tỉ số khối lượng Mặt Trời : khối lượng Trái Đất
Khối lượng của Mặt Trời gấp khoảng số lần khối lượng Trái Đất là:
\(\frac{{1{\rm{ }}988{\rm{ }}550{\rm{ }}.{\rm{ }}{{10}^{21}}}}{{0,{{6.10}^{22}}}} = \frac{{1{\rm{ }}988{\rm{ }}550{\rm{ }}.{\rm{ }}{{10}^{21}}}}{{{{6.10}^{21}}}} = \frac{1{\rm{ }}988{\rm{ }}550}{6} = 331425\) ( lần)
Tìm x biết: (2x+1)3 – 1 = -344
-
A.
x = 7
-
B.
x = -7
-
C.
x = 3
-
D.
x = -4
Đáp án : D
Đưa về dạng A3 = B3, rồi suy ra A = B
(2x+1)3 – 1 = -344
(2x+1)3 = -344 + 1
(2x+1)3 = -343
(2x+1)3 = (-7)3
2x + 1 = -7
2x = -7 – 1
2x = -8
x = -4
Vậy x = -4
Tính giá trị biểu thức \(M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\) tại x = 3
-
A.
-54
-
B.
\(\frac{{ - 1}}{{54}}\)
-
C.
\(\frac{7}{{108}}\)
-
D.
\( - \frac{2}{9}\)
Đáp án : B
Thay giá trị x = 3 vào biểu thức rồi tính
Thay x = 3 vào M ta được:
\(\begin{array}{l}M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\\ = \frac{{ - {3^2} + 2.3 - 1}}{{{{(2.3)}^3}}}\\ = \frac{{ - 9 + 6 - 1}}{{{6^3}}}\\ = \frac{{ - 4}}{{216}}\\ = \frac{{ - 1}}{{54}}\end{array}\)
Chọn câu sai. Với hai số hữu tỉ \(a,\,b\) và các số tự nhiên \(m,\,n\) ta có
-
A.
${a^m}.{a^n} = {a^{m + n}}$
-
B.
${\left( {a.b} \right)^m} = {a^m}.{b^m}$
-
C.
\({\left( {{a^m}} \right)^n} = {a^{m + n}}\)
-
D.
${\left( {{a^m}} \right)^n} = {a^{m.n}}$
Đáp án : C
Ta có ${a^m}.{a^n} = {a^{m + n}}$, ${\left( {a.b} \right)^m} = {a^m}.{b^m}$ và \({\left( {{a^m}} \right)^n} = {a^{m.n}}\) nên C sai.
Tính \({\left( {\dfrac{2}{3}} \right)^3}\)
-
A.
$\dfrac{8}{9}$
-
B.
$\dfrac{8}{{27}}$
-
C.
\(\dfrac{4}{9}\)
-
D.
$\dfrac{4}{{27}}$
Đáp án : B
Sử dụng công thức \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\)
Ta có \({\left( {\dfrac{2}{3}} \right)^3}\)\( = \dfrac{{{2^3}}}{{{3^3}}} = \dfrac{8}{{27}}\)
Chọn khẳng định đúng. Với số hữu tỉ \(x\) ta có
-
A.
${x^0} = x$
-
B.
${x^1} = 1$
-
C.
\({x^0} = 0\)
-
D.
${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$
Đáp án : D
Ta có \({x^1} = x;\)\({x^0} = 1\)\(\left( {x \ne 0} \right)\) nên A, B, C sai
${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$ nên D đúng.
Kết quả của phép tính \({\left( {\dfrac{1}{7}} \right)^2}{.7^2}\) là:
-
A.
$7$
-
B.
$\dfrac{1}{{49}}$
-
C.
\(\dfrac{1}{7}\)
-
D.
$1$
Đáp án : D
Sử dụng công thức ${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$ rồi thực hiện phép nhân.
Ta có \({\left( {\dfrac{1}{7}} \right)^2}{.7^2} = \dfrac{1}{{{7^2}}}{.7^2} = \dfrac{{{7^2}}}{{{7^2}}} = 1\)
Chọn câu sai.
-
A.
${\left( {-2019} \right)^0} = 1$
-
B.
$\left( {0,5} \right).{\left( {0,5} \right)^2} = \dfrac{1}{4}$
-
C.
${4^6}:{\rm{ }}{4^4} = 16$
-
D.
${\left( {-3} \right)^3}.{\left( {-{\rm{ }}3} \right)^{{\rm{ }}2}} = {\left( { - 3} \right)^5}$
Đáp án : B
Sử dụng công thức lũy thừa để tính toán:
\({x^1} = x;\)\({x^0} = 1\)\(\left( {x \ne 0} \right)\)
\({x^m}.{x^n} = {x^{m + n}}\); \({x^m}:{x^n} = {x^{m - n}}\)\(\left( {x \ne 0,m \ge n} \right)\)
Ta có ${\left( {-2019} \right)^0} = 1$ nên A đúng.
+) ${4^6}:{\rm{ }}{4^4} = {4^2} = 16$ nên C đúng
+) ${\left( {-3} \right)^3}.{\left( {-{\rm{ }}3} \right)^{{\rm{ }}2}} = {\left( { - 3} \right)^{3 + 2}} = {\left( { - 3} \right)^5}$nên D đúng
+) $\left( {0,5} \right).{\left( {0,5} \right)^2} = {\left( {0,5} \right)^3} = {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{1}{8}$ nên B sai.
Số ${x^{12}}$ (với $x \ne 0$) không bằng số nào trong các số sau đây ?
-
A.
${x^{18}}:{x^6}(x\; \ne 0)$
-
B.
${x^4}.{\rm{ }}{x^8}$
-
C.
${x^2}.{\rm{ }}{x^6}$
-
D.
${\left( {{x^3}} \right)^4}$
Đáp án : C
Ta áp dụng các công thức sau: ${x^m}.{x^n} = {x^{m + n}};{x^m}:{x^n} = {x^{m - n}}$$\left( {m \ge n,x \ne 0;m,n \in {N^ * }} \right)$, ${\left( {{x^m}} \right)^n} = {x^{m.n}}$
Ta có
+) ${x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}(x\; \ne 0)$ nên A đúng.
+) ${x^4}.{\rm{ }}{x^8} = {x^{4 + 8}} = {x^{12}}$ nên B đúng.
+ ${\left( {{x^3}} \right)^4} = {x^{3.4}} = {x^{12}}$ nên D đúng.
Ta thấy ở đáp án C: \({x^2}.{x^6} = {x^{2 + 6}} = {x^8} \ne {x^{12}}\)
nên C sai.
Số ${2^{24}}$ viết dưới dạng lũy thừa có số mũ $8$ là:
-
A.
${8^8}$
-
B.
${9^8}$
-
C.
${6^8}$
-
D.
Một đáp số khác
Đáp án : A
Áp dụng công thức ${\left( {{x^m}} \right)^n} = {x^{m.n}}$để tính toán
Ta có: \({2^{24}} = {2^{3.8}} = {\left( {{2^3}} \right)^8} = {8^8}\)
Số $x$ sao cho ${2^x}\; = {\left( {{2^2}} \right)^5}$ là :
-
A.
\(5\)
-
B.
$7$
-
C.
${2^7}$
-
D.
$10$
Đáp án : D
Áp dụng công thức lũy thừa của lũy thừa \({({x^m})^n} = {x^{m.n}}\) đưa hai lũy thừa về cùng cơ số và so sánh số mũ.
${2^x}\; = {\left( {{2^2}} \right)^5} \Leftrightarrow {2^x} = {2^{2.5}} \Leftrightarrow {2^x} = {2^{10}} \Leftrightarrow x = 10$
Số $a$ thỏa mãn $a:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$ là :
-
A.
$\dfrac{1}{3}$
-
B.
${\left( {\dfrac{1}{3}} \right)^7}$
-
C.
${\left( {\dfrac{1}{3}} \right)^6}$
-
D.
$\dfrac{1}{{18}}$
Đáp án : B
Áp dụng công thức nhân hai lũy thừa cùng cơ số ${x^m}.{x^n} = {x^{m + n}}$
$a{\rm{ }}:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$
$a = {\left( {\dfrac{1}{3}} \right)^3}.{\left( {\dfrac{1}{3}} \right)^4}$
$a = {\left( {\dfrac{1}{3}} \right)^{3 + 4}}$
$a = {\left( {\dfrac{1}{3}} \right)^7}$
Giá trị nhỏ nhất của biểu thức ${\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}}$ đạt được là:
-
A.
$ - \dfrac{1}{2}$
-
B.
$\dfrac{{ - 1}}{{100}}$
-
C.
$\dfrac{1}{{100}}$
-
D.
$\dfrac{{81}}{{100}}$
Đáp án : C
Dùng phương pháp đánh giá biểu thức, sử dụng \({x^2} \ge 0,\forall x\).
Ta có: ${\left( {x + \dfrac{1}{3}} \right)^2} \ge 0 $ với mọi $x$
$\Rightarrow {\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}} \ge 0+ \dfrac{1}{{100}}$
$\Rightarrow {\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}} \ge \dfrac{1}{{100}}$
Do đó GTNN biểu thức đạt được là \(\dfrac{1}{{100}}\) khi và chỉ khi
\((x + \dfrac{1}{3})^2 = 0\) \(\Rightarrow x + \dfrac{1}{3} = 0\) hay \(x = - \dfrac{1}{3}\).
Vậy giá trị nhỏ nhất cần tìm là $\dfrac{1}{100}.$
Cho ${20^n}\;:\;{5^n} = 4$ thì :
-
A.
$n = 0$
-
B.
$n = 3$
-
C.
$n = 2$
-
D.
$n = 1$
Đáp án : D
Áp dụng công thức ${x^m}:{y^m} = {\left( {x:y} \right)^m}$$\left( {y \ne 0;m \in {N^ * }} \right)$
\({20^n}\;:\;{5^n} = 4\)
\({(20:5)^n} = 4\)
\({4^n} = 4\)
\(n = 1\)
Cho biểu thức $A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}}$. Chọn khẳng định đúng.
-
A.
$A > 1$
-
B.
$A < 1$
-
C.
$A > 2$
-
D.
$A = 1$
Đáp án : B
Ta áp dụng công thức sau để tính toán
* ${x^m}.{x^n} = \underbrace {x.x.x....x}_m.\underbrace {x...x}_n = {x^{m + n}}$
*${x^m}:{x^n} = \dfrac{{{x^m}}}{{{x^n}}} = {x^{m - n}}$ ($m \ge n$)
* \({x^{m.n}} = {\left( {{x^m}} \right)^n}\)
$A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}} = \dfrac{{{2^7}.{{\left( {{3^2}} \right)}^3}}}{{{2^5}{{.3}^5}.{{\left( {{2^3}} \right)}^2}}} = \dfrac{{{2^7}{{.3}^6}}}{{{2^5}{{.2}^6}{{.3}^5}}} = \dfrac{{{2^7}{{.3}^6}}}{{{2^{11}}{{.3}^5}}} = \dfrac{{1.3}}{{{2^4}.1}} = \dfrac{3}{{16}}$
Giá trị của biểu thức \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}}\) là
-
A.
$\dfrac{4}{5}$
-
B.
$\dfrac{5}{4}$
-
C.
$\dfrac{{22}}{{30}}$
-
D.
$\dfrac{{15}}{{11}}$
Đáp án : A
Sử dụng công thức \({x^{m.n}} = {\left( {{x^m}} \right)^n}\) và \({\left( {x.y} \right)^m} = {x^m}.{y^m}\) để biển đổi và tính toán.
Ta có \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}} = \dfrac{{{{\left( {{2^2}} \right)}^6}.{{\left( {{3^2}} \right)}^5} + {6^9}.120}}{{{{\left( {{2^3}} \right)}^4}{{.3}^{12}} - {6^{11}}}}\)\( = \dfrac{{{2^{12}}{{.3}^{10}} + {6^9}.6.20}}{{{2^{12}}{{.3}^{12}} - {6^{11}}}} = \dfrac{{{2^2}{{.2}^{10}}{{.3}^{10}} + {6^{10}}.20}}{{{{\left( {2.3} \right)}^{12}} - {6^{11}}}}\)\( = \dfrac{{{2^2}{{.6}^{10}} + {6^{10}}.20}}{{{6^{12}} - {6^{11}}}}\)\( = \dfrac{{{6^{10}}\left( {{2^2} + 20} \right)}}{{{6^{10}}\left( {{6^2} - 6} \right)}} = \dfrac{{24}}{{30}} = \dfrac{4}{5}\)
Tìm \(x\), biết \({\left( {5x - 1} \right)^6} = 729\)
-
A.
\(x = \dfrac{4}{5}\); \(x = \dfrac{2}{5}\)
-
B.
\(x = - \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
-
C.
\(x = \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
-
D.
\(x = - \dfrac{4}{5}\); \(x = \dfrac{2}{5}\)
Đáp án : C
Áp dụng các công thức sau để tìm $x$
*${x^{2n}} = {a^{2n}} \Rightarrow x = a$ hoặc $x = - a$
*${x^{2n + 1}} = {a^{2n + 1}} \Rightarrow x = a$
\({\left( {5x - 1} \right)^6} = 729\)
\({\left( {5x - 1} \right)^6} = {(3)^6}\)
Trường hợp 1:
$\begin{array}{l}5x-1 = 3\\5x = 4\\x = \dfrac{4}{5}\end{array}$
Trường hợp 2:
$\begin{array}{l}5x-1 = - 3\\5x = - 2\\x = - \dfrac{2}{5}\end{array}$
Vậy \(x = \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = - 0,001\)?
-
A.
$0$
-
B.
$1$
-
C.
$2$
-
D.
$3$
Đáp án : B
Nếu \(n \in N\) lẻ mà \({a^n} = {b^n}\) thì \(a = b\)
\({\left( {2x + 1} \right)^3} = - {0,1^3} = {\left( { - 0,1} \right)^3}\)
\(2x + 1 = - 0,1\)
\(2x = - 0,1 - 1\)
\(2x = - 1,1\)
\(x = - 1,1:2\)
\(x = - 0,55\)
Vậy $x = - 0,55$.
Vậy có 1 giá trị của x.
Tìm số tự nhiên \(n\) thỏa mãn \({5^n} + {5^{n + 2}} = 650\).
-
A.
$n = 1$
-
B.
$n = 2$
-
C.
$n = 3$
-
D.
$n = 4$
Đáp án : B
Áp dụng công thức sau để tìm $n$
$a \ne 0;a \ne \pm 1$ , nếu ${a^m} = {a^n}$ thì $m = n$
\({5^n} + {5^{n + 2}} = 650\)
\({5^n} + {5^n}{.5^2} = 650\)
\({5^n}\left( {1 + {5^2}} \right) = 650\)
\({5^n}\left( {1 + 25} \right) = 650\)
\({5^n}.26 = 650\)
\({5^n} = 650:26\)
\({5^n} = 25\)
\({5^n} = {5^2}\)
\(n = 2\)
Vậy $n = 2$
Cho biết : \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\) . Tính nhanh giá trị của biểu thức sau:
\(S = \left( {{{12}^2} + {{14}^2} + {{16}^2} + {{18}^2} + {{20}^2}} \right) - \left( {{1^2} + {3^2} + {5^2} + {7^2} + {9^2}} \right)\)
-
A.
$1155$
-
B.
$5511$
-
C.
$5151$
-
D.
$1515$
Đáp án : A
Ta biến đổi biểu thức cần tính sao cho xuất hiện giả thiết đề bài cho. Từ đó thay vào ta sẽ tính được giá trị của biểu thức
Ta có: \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\)
Suy ra \({1^2} + {3^2} + {5^2} + {7^2} + {9^2} = 385 - \left( {{2^2} + {4^2} + {6^2} + {8^2} + {{10}^2}} \right) = 385 - {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2}} \right)\)
Và \({12^2} + {14^2} + {16^2} + {18^2} + {20^2} = {2^2}.\left( {{6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right)\)
Suy ra \(\) \(S = {2^2}.\left( {{6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right) - 385 + {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2}} \right)\)
\(S = {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2} + {6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right) - 385 = 4.385 - 385 = 1155\)
Vậy $S{\rm{ }} = {\rm{ }}1155$.
Cho \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\). Chọn đáp án đúng.
-
A.
\(A\) không phải là một số nguyên
-
B.
\(A\) là một số nguyên
-
C.
\(A\) là một số nguyên dương
-
D.
\(A\) là một số nguyên âm
Đáp án : A
+ Nhân \(A\) với \(\dfrac{3}{4}\) rồi thực hiện cộng \(A\) với \(\dfrac{3}{4}A\), sau đó thu gọn kết quả và suy ra \(A\).
+ Sử dụng: Khi \(0 < a < 1\) và \(m > n > 0\) thì \({a^m} < {a^n}\) để đánh giá \(A\)
\(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\)
\( \Rightarrow \dfrac{3}{4}A = \dfrac{3}{4} - {\left( {\dfrac{3}{4}} \right)^2} + {\left( {\dfrac{3}{4}} \right)^3} - {\left( {\dfrac{3}{4}} \right)^4} + ...\) \( + {\left( {\dfrac{3}{4}} \right)^{2017}} - {\left( {\dfrac{3}{4}} \right)^{2018}} + {\left( {\dfrac{3}{4}} \right)^{2019}}\)
\( \Rightarrow A + \dfrac{3}{4}A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\)
\( \Rightarrow \left( {1 + \dfrac{3}{4}} \right)A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\)
\( \Rightarrow \dfrac{7}{4}.A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\)
\( \Rightarrow A = \left[ {1 + {{\left( {\dfrac{3}{4}} \right)}^{2019}}} \right]:\dfrac{7}{4} = \left[ {1 + {{\left( {\dfrac{3}{4}} \right)}^{2019}}} \right].\dfrac{4}{7}\)
Suy ra \(A > 0\,\,\,\,\,\,\,\left( 1 \right)\)
Vì \({\left( {\dfrac{3}{4}} \right)^{2019}} < \dfrac{3}{4} \Rightarrow A < \left( {1 + \dfrac{3}{4}} \right).\dfrac{4}{7} = 1\,\,\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(0 < A < 1\).
Vậy \(A\) không phải là số nguyên.
Luyện tập và củng cố kiến thức Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Cộng, trừ, nhân, chia số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tập hợp các số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 36: Hình hộp chữ nhật và hình lập phương Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 33: Quan hệ giữa ba cạnh trong một tam giác Toán 7 Kết nối tri thức
