Trắc nghiệm Bài 1: Tập hợp các số hữu tỉ Toán 7 Kết nối tri thức
Đề bài
Tập hợp các số hữu tỉ được kí hiệu là:
-
A.
\(\mathbb{R}\)
-
B.
\(\mathbb{Q}\)
-
C.
\(\mathbb{I}\)
-
D.
\(\mathbb{N}\)
Số \(\dfrac{9}{4}\) có số đối là:
-
A.
\(\dfrac{4}{9}\)
-
B.
\(\dfrac{{ - 4}}{9}\)
-
C.
\(\dfrac{9}{{ - 4}}\)
-
D.
\(2,25\)
Khẳng định nào sau đây là đúng?
-
A.
Nếu a > b thì –a > - b
-
B.
Nếu a < b, a < c thì b < c
-
C.
Nếu a < b; c > b thì a < c
-
D.
Số hữu tỉ gồm: số hữu tỉ dương và số hữu tỉ âm
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35
-
A.
\( - \frac{3}{5}\)
-
B.
\(\frac{7}{{20}}\)
-
C.
- \(\frac{7}{{20}}\)
-
D.
\(\frac{{ - 35}}{{10}}\)
Biểu diễn các số: \( - 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
-
A.
5
-
B.
4
-
C.
3
-
D.
2
Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:
-
A.
\(\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}\)
-
B.
\(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\)
-
C.
\(\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}\)
-
D.
\(\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}\)
-
A.
a < 0
-
B.
a > 0
-
C.
a = 0
-
D.
a\( \ge \)0
Có mấy giá trị x nguyên thỏa mãn: \(\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\)
-
A.
0
-
B.
2
-
C.
4
-
D.
6
Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây.
Hỏi bạn nào chạy nhanh nhất?
-
A.
An
-
B.
Bình
-
C.
Chi
-
D.
Duy
Cho số hữu tỉ \(x = \frac{7}{{n + 2}}\)
Tìm tổng của các số nguyên n sao cho x là một số nguyên
-
A.
-4
-
B.
4
-
C.
0
-
D.
-8
Cho số hữu tỉ \(y = \dfrac{{2a - 1}}{{ - 3}}.\) Với giá trị nào của $a$ thì $y$ không là số dương và cũng không là số âm.
-
A.
$1$
-
B.
$\dfrac{1}{2}$
-
C.
$2$
-
D.
$4$
Cho số hữu tỉ \(x = \dfrac{{a - 3}}{2}.\) Với giá trị nào của $a$ thì $x$ là số nguyên dương;
-
A.
$a = 3 - 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
B.
$a = 3 + k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
C.
$a = 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
D.
$a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
Trong các phân số \(\dfrac{{14}}{{18}}\,\,;\,\,\dfrac{{24}}{{26}}\,\,;\,\,\dfrac{{26}}{{ - 28}}\,\,;\,\,\dfrac{{ - 28}}{{30}}\,\,;\,\,\dfrac{{72}}{{78}}\) có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{13}}\) ?
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
-
A.
1 điểm
-
B.
4 điểm
-
C.
3 điểm
-
D.
2 điểm
So sánh \(x = \dfrac{{2002}}{{2003}}\) và \(y = \dfrac{{14}}{{13}}\)
-
A.
$y = x$
-
B.
$y < x$
-
C.
$y > x$
-
D.
$x \ge y$
So sánh hai số \(x = \dfrac{2}{{ - 5}}\) và \(y = \dfrac{{ - 3}}{{13}}\)
-
A.
$x > y$
-
B.
$x < y$
-
C.
$x = y$
-
D.
$x \ge y$
Số hữu tỉ lớn nhất trong các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) là:
-
A.
$\dfrac{7}{8}$
-
B.
$\dfrac{3}{4}$
-
C.
$\dfrac{{18}}{{19}}$
-
D.
$\dfrac{{27}}{{28}}$
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: \(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
-
A.
\(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
-
B.
\(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 16}}{{17}}\)
-
C.
\(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 16}}{{17}}\)
-
D.
\(\dfrac{{ - 16}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 1}}{{17}}\)
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn số hữu tỉ âm
(II) Số hữu tỉ dương lớn hơn số tự nhiên
(III) Số $0$ là số hữu tỉ âm
(IV) Số nguyên dương là số hữu tỉ.
Số các câu đúng trong các câu trên là
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
-
A.
$\dfrac{6}{9}$
-
B.
$\dfrac{9}{{12}}$
-
C.
$\dfrac{{ - \;6}}{{ - \,8}}$
-
D.
$\dfrac{{ - \,3}}{{ - \,4}}$
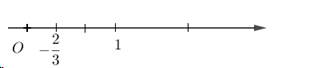
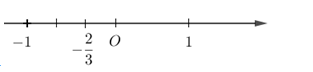
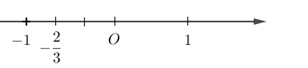
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
-
A.
-
B.
-
C.

-
D.
Số nào dưới đây là số hữu tỉ dương?
-
A.
$\dfrac{{ - 2}}{{ - 3}}$
-
B.
$\dfrac{{ - \,2}}{5}$
-
C.
$\dfrac{{ - \,5}}{{15}}$
-
D.
$\dfrac{2}{{ - 15}}$
Chọn câu đúng
-
A.
$\dfrac{3}{2} \in Q$
-
B.
$\dfrac{2}{3} \in Z$
-
C.
$ - \dfrac{9}{2} \notin Q$
-
D.
$ - \;6 \in N$
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
-
A.
\(a = 0\,;b \ne 0\)
-
B.
\(a,b \in Z,b \ne 0\)
-
C.
\(a,b \in N\)
-
D.
\(a \in N,b \ne 0\)
Lời giải và đáp án
Tập hợp các số hữu tỉ được kí hiệu là:
-
A.
\(\mathbb{R}\)
-
B.
\(\mathbb{Q}\)
-
C.
\(\mathbb{I}\)
-
D.
\(\mathbb{N}\)
Đáp án : B
Kí hiệu các tập hợp số
Tập hợp các số hữu tỉ được kí hiệu là: Q
Kí hiệu Q của tập hợp các số hữu tỉ được coi như là chữ viết tắt của quoziente, nghĩa là tỷ lệ
Số \(\dfrac{9}{4}\) có số đối là:
-
A.
\(\dfrac{4}{9}\)
-
B.
\(\dfrac{{ - 4}}{9}\)
-
C.
\(\dfrac{9}{{ - 4}}\)
-
D.
\(2,25\)
Đáp án : C
2 số đối nhau là 2 số có tổng bằng 0.
Số đối của số hữu tỉ a là -a
Số đối của \(\dfrac{9}{4}\) là \( - \dfrac{9}{4} = \dfrac{9}{{ - 4}}\)
Khẳng định nào sau đây là đúng?
-
A.
Nếu a > b thì –a > - b
-
B.
Nếu a < b, a < c thì b < c
-
C.
Nếu a < b; c > b thì a < c
-
D.
Số hữu tỉ gồm: số hữu tỉ dương và số hữu tỉ âm
Đáp án : C
Tính chất, thứ tự trên tập hợp các só hữu tỉ
+) Nếu a > b thì –a < -b nên A sai
+) Nếu a < b, a < c thì chưa thể so sánh được b với c nên B sai
+) Nếu a < b, c > b ( hay b < c) thì a < c ( tính chất bắc cầu) nên C đúng
+) Số hữu tỉ gồm: số hữu tỉ âm, số hữu tỉ dương và số 0 nên D sai.
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35
-
A.
\( - \frac{3}{5}\)
-
B.
\(\frac{7}{{20}}\)
-
C.
- \(\frac{7}{{20}}\)
-
D.
\(\frac{{ - 35}}{{10}}\)
Đáp án : C
Biểu diễn số thập phân dưới dạng phân số:
+ Viết số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10
+ Rút gọn phân số.
Ta có:
\( - 0,35 = \frac{{ - 35}}{{100}} = \frac{{( - 35):5}}{{100:5}} = \frac{{ - 7}}{{20}}\)
Biểu diễn các số: \( - 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
-
A.
5
-
B.
4
-
C.
3
-
D.
2
Đáp án : B
+ Đưa các số về dạng phân số tối giản rồi xác định các số bằng nhau.
+ Các số bằng nhau chỉ được biểu diễn bởi một điểm trên trục số.
Ta có:
\(\begin{array}{l} - 0,4 = \frac{{ - 4}}{{10}} = \frac{{ - 4:2}}{{10:2}} = \frac{{ - 2}}{5};\\\frac{8}{{20}} = \frac{{8:4}}{{20:4}} = \frac{2}{5};\\\frac{{12}}{{ - 20}} = \frac{{12:( - 4)}}{{( - 20):( - 4)}} = \frac{{ - 3}}{5};\\\frac{{ - 3}}{8};\\ - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{( - 375):125}}{{1000:125}} = \frac{{ - 3}}{8}\end{array}\)
Ta có các điểm biểu diễn khác nhau là \(\frac{{ - 2}}{5}; \frac{2}{5}; \frac{{ - 3}}{5}; \frac{{ - 3}}{8}\)
Vậy các số trên biểu diễn 4 số hữu tỉ khác nhau nên được biểu diễn bởi 4 điểm khác nhau trên trục số
Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:
-
A.
\(\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}\)
-
B.
\(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\)
-
C.
\(\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}\)
-
D.
\(\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}\)
Đáp án : A
+ Dùng tính chất: Nếu a < b thì –a > - b
+ Các phân số có cùng mẫu số dương: phân số nào có tử số lớn hơn thì phân số đó lớn hơn
+ Các phân số dương có cùng tử số: phân số nào có mẫu số lớn hơn thì nhỏ hơn
+ So sánh \(\frac{5}{{ - 20}}\) và \( \frac{{ - 5}}{{17}}\):
Vì 20 > 17 nên \(\frac{5}{{20}} < \frac{5}{{17}}\), do đó \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}\)
+ So sánh \(\frac{ - 5}{17}\) và \(\frac{1}{{ - 3}}\):
Vì \(\frac{5}{{17}} < \frac{5}{{15}}\) nên \(\frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}\)
+ So sánh \(\frac{1}{ - 3}\) và \(\frac{{ - 7}}{{20}}\):
Vì \(\frac{7}{{20}} > \frac{7}{{21}}\) nên \(\frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}\)
Do đó, \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}\)
-
A.
a < 0
-
B.
a > 0
-
C.
a = 0
-
D.
a\( \ge \)0
Đáp án : B
Số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ dương khi a, b cùng dấu
Nhận xét về mẫu số của phân số
\(x = \frac{a}{{2{a^2} + 1}}\) là số hữu tỉ dương thì \(x = \frac{a}{{2{a^2} + 1}} > 0\)
Ta có:
a2 \( \ge \)0, với mọi a nên 2a2 + 1 \( \ge \)1 > 0, với mọi a
Như vậy, để \(x = \frac{a}{{2{a^2} + 1}}\) > 0 thì a > 0
Có mấy giá trị x nguyên thỏa mãn: \(\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\)
-
A.
0
-
B.
2
-
C.
4
-
D.
6
Đáp án : B
Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số, suy ra điều kiện của x
Ta có:
\(\begin{array}{l}\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 3}}{7} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 6}}{{14}} > \frac{{2x}}{{14}} > \frac{{ - 11}}{{14}}\\ - 6 > 2x > - 11\\ - 3 > x > - \frac{{11}}{2}\end{array}\)
\( - 3 > x > - 5,5\)
Mà x nguyên nên \(x \in \{ - 4; - 5\} \)
Vậy có 2 giá trị x thỏa mãn
Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây.
Hỏi bạn nào chạy nhanh nhất?
-
A.
An
-
B.
Bình
-
C.
Chi
-
D.
Duy
Đáp án : B
So sánh thành tích của các bạn: So sánh các số hữu tỉ
Bạn nào có thời gian chạy nhỏ nhất thì bạn đó chạy nhanh nhất.
Ta có: \(\frac{1}{3}\)phút = \(\frac{1}{3}\) . 60 = 20 giây
\(\frac{{108}}{5}\) giây = 21,6 giây
\(20\frac{3}{8}\) giây = 20,375 giây
Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất
+ Đưa các số liệu về cùng đơn vị rồi mới so sánh
+ Nếu các số hữu tỉ viết được dưới dạng số thập phân thì ta viết chúng ở dạng số thập phân rồi so sánh.
Cho số hữu tỉ \(x = \frac{7}{{n + 2}}\)
Tìm tổng của các số nguyên n sao cho x là một số nguyên
-
A.
-4
-
B.
4
-
C.
0
-
D.
-8
Đáp án : D
Để x là số nguyên thì \(7 \vdots (n + 2)\) hay \((n + 2) \in \) Ư (7) = {1; -1; 7; -7}
Để x là số nguyên thì \(7 \vdots (n + 2)\) hay \((n + 2) \in \) Ư (7) = {1; -1; 7; -7}
Ta có bảng sau:
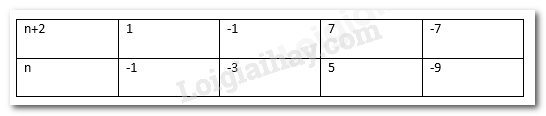
Vậy có 4 giá trị n thỏa mãn điều kiện.
Tổng của các giá trị n đó là: (-1) + (-3) + 5 + (-9) = -8
Cho số hữu tỉ \(y = \dfrac{{2a - 1}}{{ - 3}}.\) Với giá trị nào của $a$ thì $y$ không là số dương và cũng không là số âm.
-
A.
$1$
-
B.
$\dfrac{1}{2}$
-
C.
$2$
-
D.
$4$
Đáp án : B
Số hữu tỉ \(0\) không là số dương cũng không là số âm. Nên ta cho $y=0$ từ đó tìm $a.$
Vì số hữu tỉ \(0\) không là số dương cũng không là số âm nên để \(y = \dfrac{{2a - 1}}{{ - 3}}\) không dương cũng không âm thì
\(y = 0\) suy ra \(\dfrac{{2a - 1}}{{ - 3}} = 0\) nên \(2a - 1 = 0 \) do đó \(a = \dfrac{1}{2}\) .
Cho số hữu tỉ \(x = \dfrac{{a - 3}}{2}.\) Với giá trị nào của $a$ thì $x$ là số nguyên dương;
-
A.
$a = 3 - 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
B.
$a = 3 + k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
C.
$a = 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
-
D.
$a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
Đáp án : D
Số hữu tỉ \(\dfrac{a}{b}\) là số nguyên dương khi \(a,\,b\) cùng dấu và \(a \vdots b\).
Để \(x = \dfrac{{a - 3}}{2}\) là số nguyên dương thì \(\left( {a - 3} \right) > 0\) và \(\left( {a - 3} \right) \vdots 2\)
Giả sử \(a - 3 = 2k\,\left( {k \in {\mathbb{N}^*}} \right)\) suy ra \(a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)\)
Trong các phân số \(\dfrac{{14}}{{18}}\,\,;\,\,\dfrac{{24}}{{26}}\,\,;\,\,\dfrac{{26}}{{ - 28}}\,\,;\,\,\dfrac{{ - 28}}{{30}}\,\,;\,\,\dfrac{{72}}{{78}}\) có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{13}}\) ?
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
Rút gọn các phân số sau đó so sánh các phân số đó với \(\dfrac{{12}}{{13}}\) .
\(\dfrac{{14}}{{18}} = \dfrac{7}{9}\,;\,\dfrac{{24}}{{26}} = \dfrac{{12}}{{13}}\,\,;\,\dfrac{{72}}{{78}} = \dfrac{{12}}{{13}}.\)
Ta có \(\dfrac{{26}}{{ - 28}} < 0 < \dfrac{{12}}{{13}};\,\dfrac{{ - 28}}{{30}} < 0 < \dfrac{{12}}{{13}}\) ; \(\dfrac{7}{9} = \dfrac{{91}}{{117}} < \dfrac{{108}}{{117}} = \dfrac{{12}}{{13}}\)
Vậy có 2 phân số bằng phân số \(\dfrac{{12}}{{13}}\) là: \(\dfrac{{24}}{{26}}\,;\,\dfrac{{72}}{{78}}.\)
Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
-
A.
1 điểm
-
B.
4 điểm
-
C.
3 điểm
-
D.
2 điểm
Đáp án : A
+ Rút gọn các phân số, đưa về cùng mẫu và so sánh các phân số
+ Sử dụng: Các số hữu tỉ bằng nhau được biểu diễn bởi cùng một điểm trên trục số.
$0,25 = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{ - 25}}{{ - 100}} = \dfrac{1}{4};\dfrac{5}{{20}} = \dfrac{1}{4}.$
Nên \(\dfrac{1}{4} = 0,25 = \dfrac{{ - 25}}{{ - 100}} = \dfrac{5}{{20}}\)
Do đó các số \(\dfrac{1}{4};0,25\,;\,\dfrac{{ - 25}}{{ - 100}}\,;\,\dfrac{5}{{20}}\) được biểu diễn cùng một điểm trên trục số.
Một số em chưa so sánh các số mà kết luận luôn \(4\) điểm là sai.
So sánh \(x = \dfrac{{2002}}{{2003}}\) và \(y = \dfrac{{14}}{{13}}\)
-
A.
$y = x$
-
B.
$y < x$
-
C.
$y > x$
-
D.
$x \ge y$
Đáp án : C
So sánh với số \(1\)
Ta có \(x = \dfrac{{2002}}{{2003}} < \dfrac{{2003}}{{2003}} = 1\) hay \(x < 1\)
Và \(y = \dfrac{{14}}{{13}} > \dfrac{{13}}{{13}} = 1\) hay \(y > 1\)
Từ đó suy ra \(y > 1 > x\) hay \(y > x\) .
So sánh hai số \(x = \dfrac{2}{{ - 5}}\) và \(y = \dfrac{{ - 3}}{{13}}\)
-
A.
$x > y$
-
B.
$x < y$
-
C.
$x = y$
-
D.
$x \ge y$
Đáp án : B
Đưa hai phân số về cùng mẫu dương rồi so sánh hai tử số với nhau.
Ta có \(x = \dfrac{2}{{ - 5}} = \dfrac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \dfrac{{ - 26}}{{65}}\) và $y = \dfrac{{ - 3}}{{13}} = \dfrac{{ - 3.5}}{{13.5}} = \dfrac{{ - 15}}{{65}}$
Mà \( - 26 < - 15 \) suy ra \(\dfrac{{ - 26}}{{65}} < \dfrac{{ - 15}}{{65}}\) hay \(x < y\) .
Số hữu tỉ lớn nhất trong các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) là:
-
A.
$\dfrac{7}{8}$
-
B.
$\dfrac{3}{4}$
-
C.
$\dfrac{{18}}{{19}}$
-
D.
$\dfrac{{27}}{{28}}$
Đáp án : D
So sánh các số hữu tỉ dựa vào phần bù với \(1\). Số nào có phần bù với \(1\) nhỏ nhất thì số đó lớn nhất.
Lưu ý: Trong các phân số dương có cùng tử số dương, phân số nào có mẫu lớn hơn thì nhỏ hơn.
Phần bù với \(1\) của các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) lần lượt là \(\dfrac{1}{8};\,\dfrac{1}{3};\dfrac{1}{4};\dfrac{1}{{19}};\dfrac{1}{{28}}\)
Mà \(28 > 19 > 8 > 4 > 3\) nên \(\dfrac{1}{{28}} < \dfrac{1}{{19}} < \dfrac{1}{8} < \dfrac{1}{4} < \dfrac{1}{3}\)
Suy ra \(\dfrac{{27}}{{28}} > \dfrac{{18}}{{19}} > \dfrac{7}{8} > \dfrac{3}{4} > \dfrac{2}{3}\)
Số hữu tỉ lớn nhất là: \(\dfrac{{27}}{{28}}\)
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: \(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
-
A.
\(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
-
B.
\(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 16}}{{17}}\)
-
C.
\(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 16}}{{17}}\)
-
D.
\(\dfrac{{ - 16}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 1}}{{17}}\)
Đáp án : C
Để so sánh các số hữu tỉ có cùng mẫu ta so sánh các tử số với nhau.
Phân số nào có tử số lớn hơn thì lớn hơn.
Phân số nào có tử số nhỏ hơn thì nhỏ hơn.
Vì \( - 1 > - 3 > - 9 > - 11 > - 12 > - 14 > - 16\)
Nên ta có \(\dfrac{{ - 1}}{{17}} > \dfrac{{ - 3}}{{17}} > \dfrac{{ - 9}}{{17}} > \dfrac{{ - 11}}{{17}} > \dfrac{{ - 12}}{{17}} > \dfrac{{ - 14}}{{17}} > \dfrac{{ - 16}}{{17}}\)
Vậy dãy số theo thứ tự giảm dần là \(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 16}}{{17}}\)
Một số em nhầm đáp án D vì xếp theo thứ tự tăng dần. Ở đây đề bài yêu cầu thứ tự gảm dần.
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn số hữu tỉ âm
(II) Số hữu tỉ dương lớn hơn số tự nhiên
(III) Số $0$ là số hữu tỉ âm
(IV) Số nguyên dương là số hữu tỉ.
Số các câu đúng trong các câu trên là
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
(I) đúng
(II) sai vì số hữu tỉ dương chưa chắc lớn hơn số tự nhiên. Ví dụ: \(\dfrac{5}{4} < 2\) .
(III) sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
(IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là \(1\).
Vậy có hai câu đúng.
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
-
A.
$\dfrac{6}{9}$
-
B.
$\dfrac{9}{{12}}$
-
C.
$\dfrac{{ - \;6}}{{ - \,8}}$
-
D.
$\dfrac{{ - \,3}}{{ - \,4}}$
Đáp án : A
Ta rút gọn các phân số rồi đưa các phân số về cùng mẫu số sau đó so sánh hai tử số với nhau.
\(\dfrac{6}{9} = \dfrac{2}{3}\,;\,\dfrac{9}{{12}} = \dfrac{3}{4}\,;\,\dfrac{{ - 6}}{{ - 8}} = \dfrac{3}{4}\,;\,\dfrac{{ - 3}}{{ - 4}} = \dfrac{3}{4}.\)
Vậy phân số không bằng phân số $\dfrac{3}{4}$ là \(\dfrac{6}{9}.\)
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
-
A.

-
B.

-
C.

-
D.

Đáp án : D
Sử dụng cách biểu diễn số hữu tỉ trên trục số:
Nếu \(\dfrac{-a}{b}\) là số hữu tỉ âm, ta chia khoảng có độ dài $1$ đơn vị làm $b$ phần bằng nhau, rồi lấy về phía chiều âm trục $Ox$ là $a$ phần , ta được vị trí của số \(\dfrac{-a}{b}\).
Biểu diễn số \( - \dfrac{2}{3}\) trên trục số ta được:
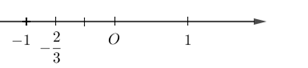
Một số em nhầm đáp án do không để ý rằng số \( - \dfrac{2}{3}\) phải nằm bên trái số \(0\).
Số nào dưới đây là số hữu tỉ dương?
-
A.
$\dfrac{{ - 2}}{{ - 3}}$
-
B.
$\dfrac{{ - \,2}}{5}$
-
C.
$\dfrac{{ - \,5}}{{15}}$
-
D.
$\dfrac{2}{{ - 15}}$
Đáp án : A
\(\begin{array}{l}\dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} > 0\,;\\\dfrac{{ - 2}}{5}\, < 0\,;\,\dfrac{{ - 5}}{{15}} < 0\,\,;\,\dfrac{2}{{ - 15}} < 0.\end{array}\)
Vậy số hữu tỉ dương là \(\dfrac{{ - 2}}{{ - 3}}.\)
Chọn câu đúng
-
A.
$\dfrac{3}{2} \in Q$
-
B.
$\dfrac{2}{3} \in Z$
-
C.
$ - \dfrac{9}{2} \notin Q$
-
D.
$ - \;6 \in N$
Đáp án : A
Ta có \( - 6 \in \mathbb{Z};-6\notin\mathbb N \) nên D sai.
\(\dfrac{2}{3} \in \mathbb{Q};\,\dfrac{2}{3} \notin \mathbb{Z}\) nên B sai.
\( - \dfrac{9}{2} \in \mathbb{Q}\) nên C sai
\(\dfrac{3}{2} \in \mathbb{Q}\) nên A đúng.
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
-
A.
\(a = 0\,;b \ne 0\)
-
B.
\(a,b \in Z,b \ne 0\)
-
C.
\(a,b \in N\)
-
D.
\(a \in N,b \ne 0\)
Đáp án : B
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) trong đó \(a,b \in Z\,;b \ne 0.\)
Luyện tập và củng cố kiến thức Bài 2: Cộng, trừ, nhân, chia số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 36: Hình hộp chữ nhật và hình lập phương Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 33: Quan hệ giữa ba cạnh trong một tam giác Toán 7 Kết nối tri thức










Danh sách bình luận