Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 9. Độ dài đường tròn, cung tròn

Đề kiểm tra 15 phút - Đề số 3 - Bài 9 - Chương 3 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 9 - Chương 3 - Hình học 9

Đề bài

Cho ba điểm A, B, C liên tiếp trên một đường thẳng. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn có đường kính AB và BC.

Phương pháp giải - Xem chi tiết

Gọi C1 là độ dài đường tròn đường kính AC, C2, C3 lần lượt là độ dài các đường tròn đường kính AB và BC.

Chứng minh \(  \dfrac{{{C_1}} }{ 2} =\dfrac {{{C_2} + {C_3}}}{ 2}\)

 

Lời giải chi tiết

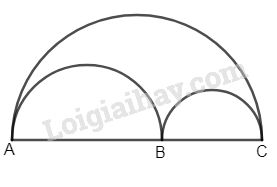
Gọi C1 là độ dài đường tròn đường kính AC, C2, C3 lần lượt là độ dài các đường tròn đường kính AB và BC.

Ta có : \(C_1= π.AC\);

           \(C_2= π.AB\);

           \(C_3= π.BC\).

Vì B nằm giữa A và C nên \(AC = AB + BC\)

Vậy \({C_2} + {C_3} = \pi AB + \pi BC \)\(\,= \pi \left( {AB + BC} \right) = \pi AC\)

\( \Rightarrow \dfrac{{{C_1}} }{ 2} =\dfrac {{{C_2} + {C_3}}}{ 2}\)

Nghĩa là độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.

 Loigiaihay.com


Bình chọn:
4 trên 5 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store