Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 10. Diện tích hình tròn, hình quạt tròn

Bài 84 trang 99 SGK Toán 9 tập 2


a) Vẽ lại hình tạo bởi các cung tròn

Đề bài

a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh \(C\) của tam giác đều \(ABC\) cạnh \(1 cm\). Nêu cách vẽ (h.63).

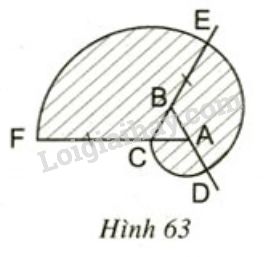
b) Tính diện tích miền gạch sọc.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Sử dụng compa và thước thẳng để vẽ hình.

+) Áp dụng công thức tính diện tích cung tròn \(n^0\) của đường tròn bán kính \(R\) là: \(S = \dfrac{{\pi {R^2}n}}{{360}}.\)

+) Áp dụng diện tích hình tròn bán kính \(R\) là \(S= \pi R^2\) 

Lời giải chi tiết

a) Vẽ tam giác đều \(ABC\) cạnh \(1cm\)

Vẽ \(\dfrac{1}{3}\) đường tròn tâm \(A\), bán kính \(1cm\), ta được cung \(\overparen{CD}\)

Vẽ cung \(\overparen{DE}\) của đường tròn tâm \(B\), bán kính \(2cm\) sao cho \(\widehat {DBE} =120^0\)

Vẽ cung \(\overparen{EF}\) của đường tròn tâm \(C\), bán kính \(3cm\) sao cho \(\widehat {ECF} =120^0\)

b) Diện tích hình quạt \(CAD\) là \(\dfrac{1}{3}\) \(π.1^2\)

Diện tích hình quạt \(DBE\) là \(\dfrac{1}{3}\) \(π.2^2\) 

Diện tích hình quạt \(ECF\) là \(\dfrac{1}{3}\) \(π.3^2\)

Diện tích phần gạch sọc là  \(\dfrac{1}{3}.π.1^2+ \dfrac{1}{3}.π.2^2 +\dfrac{1}{3}.π.3^2\)

\(=\dfrac{1}{3}\) \(π (1^2 + 2^2 + 3^2) = \dfrac{14}{3}π\) (\(cm^2\))


Bình chọn:
4.1 trên 47 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store