Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Sự xác định của đường tròn. Tính chất đối xứng c..

Bài 3 trang 100 SGK Toán 9 tập 1


Chứng minh các định lý sau:

Đề bài

Chứng minh các định lý sau:

a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng tính chất:

a) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh đó. 

b) Tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó thì là tam giác vuông.

Lời giải chi tiết

a) Xét tam giác \(ABC\) vuông tại \(A\).

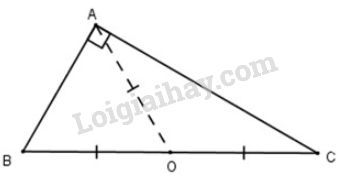
Gọi \(O\) là trung điểm của cạnh huyền \(BC\), ta có:

Vì \(\Delta{ABC}\) vuông tại \(A\) có \(AO\) là trung tuyến

\(\Rightarrow AO=BO=CO =\dfrac{BC}{2}\) ( Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

\(\Rightarrow\) 3 điểm \(A,\ B,\ C\) cùng thuộc đường tròn tâm \(O\) bán kính \(OA\)

Vậy tâm đường tròn ngoại tiếp tam giác \(ABC\) chính là trung điểm của cạnh huyền.

b) 

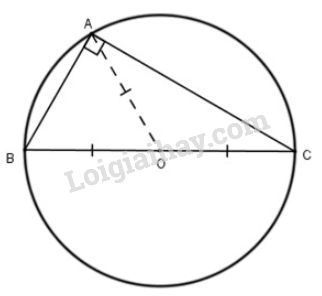
Xét tam giác \(ABC\) nội tiếp đường tròn \((O)\) đường kính \(BC\).

\(\Rightarrow OA = OB = OC = R\)

\(\Rightarrow \) Tam giác \(ABC\) có đường trung tuyến AO bằng nửa cạnh BC nên vuông tại \(A\) 

Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.


Bình chọn:
4.5 trên 142 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store