Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh v..

Bài 25 trang 119 SGK Toán 9 tập 2


Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy a,b (a

Đề bài

Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy \(a,b\) (\(a<b\)) và độ dài đường sinh là \(l\) (\(a,b,l\) có cùng đơn vị đo).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Diện tích xung quanh hình nón: \(S_{xq}=\pi r l.\) với \(r\) là bán kính đáy và \(l\) là đường sinh.

+) \(S_{xq \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn } - S_{xq \, \, hình \, \, nón \, \, nhỏ}.\)

Lời giải chi tiết

                           

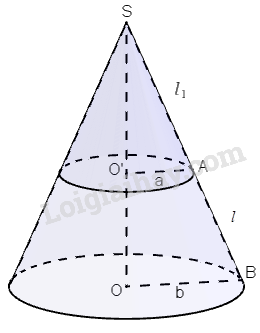
Kí hiệu như hình vẽ.  \(SA=l_1;AB=l;OB=b;O'A=a.\)

Vì \(O'A//OB \Rightarrow \dfrac{{SA}}{{SB}} = \dfrac{{O'A}}{{OB}}\)(Hệ quả định lí Talet)

\( \Leftrightarrow \dfrac{{{l_1}}}{{l + {l_1}}} = \dfrac{a}{b} \Leftrightarrow b{l_1} = al + a{l_1} \Leftrightarrow {l_1}\left( {b - a} \right) = al \Leftrightarrow {l_1} = \dfrac{a}{{b - a}}l\)

Suy ra \(SB = l + {l_1} = l + \dfrac{a}{{b - a}}l = \dfrac{b}{{b - a}}l\)

Diện tích xung quanh hình nón lớn là \({S_1} = \pi .b.SB = \pi .b.\dfrac{b}{{b - a}}l = \dfrac{{{b^2}}}{{b - a}}\pi l\)

Diện tích xung quanh hình nón nhỏ là \({S_2} = \pi .a.SA = \pi .a.\dfrac{a}{{b - a}}l = \dfrac{{{a^2}}}{{b - a}}\pi l\)

Diện tích xung quanh hình nón cụt là \(S = {S_1} - {S_2} = \dfrac{{{b^2}}}{{b - a}}\pi l - \dfrac{{{a^2}}}{{b - a}}\pi l = \pi l.\dfrac{{{b^2} - {a^2}}}{{b - a}} = \left( {a + b} \right)\pi l\)

Vậy diện tích xung quanh nón cụt là \(S = \pi \left( {a + b} \right)l\)


Bình chọn:
3.8 trên 28 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store