Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh v..

Bài 22 trang 118 SGK Toán 9 tập 2


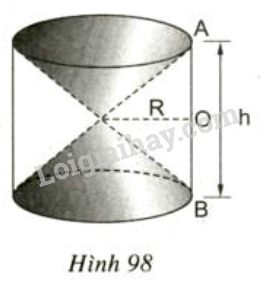
Hình 98 cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo (OA= OB).

Đề bài

Hình 98 cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo (\(OA= OB\)).

Hãy so sánh tổng thể tích của hai hình nón và thể tích hình trụ.

            

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Thể tích hình trụ bán kính đáy là \(R\) và chiều cao \(h\) là: \(V=\pi R^2h.\)

+) Thể tích hình nón bán kính đáy \(R\) và chiều cao \(h\) là: \(V=\dfrac{1}{3} \pi R^2h.\)

Lời giải chi tiết

Nhận thấy hai hình nón trên hình bằng nhau. 

Chiều cao của 1 hình nón là: \(\dfrac{h}{2}\) 

Thể tích của hai hình nón là: 

\(2{V_{nón}}\)\(=2.\dfrac{1}{3} \pi .R^2 .\dfrac{h}{2}= \dfrac{\pi R^2 h}{3}\)

Thể tích của hình trụ là: \({V_{trụ}} = \pi {R^2}h\) 

Nên \(\dfrac{2V_{nón}}{V_{trụ}}= \dfrac{\dfrac{\pi R^2 h}{3}}{\pi R^2 h}= \dfrac{1}{3}.\)

Loigiaihay.com


Bình chọn:
4.2 trên 24 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store