Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Ôn tập cuối năm - Hình học - Toán 9

Bài 13 trang 135 SGK Toán 9 tập 2


Cho đường tròn (O), cung BC có số đo bằng 120o, điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC.

Đề bài

Cho đường tròn \((O)\), cung \(BC\) có số đo bằng \(120^0\), điểm \(A\) di chuyển trên cung lớn \(BC\). Trên tia đối tia \(AB\) lấy điểm \(D\) sao cho \(AD = AC\). Hỏi điểm \(D\) di chuyển trên đường nào?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+ Tính \(\widehat {BDC}\) dựa vào tính chất góc nội tiếp rồi sử dụng quỹ tích cung chứa góc dựng trên đoạn \(BC.\)

+ Xác định giới hạn quỹ tích của điểm \(D\) rồi kết luận.

Lời giải chi tiết

                     

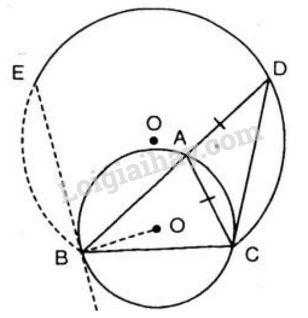
Xét đường tròn (O), có \(\displaystyle \widehat {BAC} = {1 \over 2}sđ\overparen{BC}\)\(= {60^0}\) (số đo góc nội tiếp bằng nửa số đo cung bị chắn)

Vì \(\widehat {BAC}\) là góc ngoài tại A của tam giác ACD nên \(\widehat {BAC}=\widehat {ADC} + \widehat {ACD}\)

Vì AC = AD nên tam giác ADC cân tại A. Do đó, \(\widehat {ADC} = \widehat {ACD}\)

\(\Rightarrow \widehat {ADC} = \widehat {ACD} = {1 \over 2}{.60^0} = {30^0}\)

Như vậy, điểm \(D\) tạo với hai mút của đoạn thẳng \(BC\) cố định một góc \(\widehat {B{\rm{D}}C} = {30^0}\) nên \(D\) chuyển động trên cung chứa góc \(30^0\) dựng trên \(BC.\)

Ta có, khi \(A ≡ B\) thì \(D ≡ E\) và khi \(A ≡ C\) thì \(D ≡ C.\) 

Vậy khi \(A\) di chuyển trên cung lớn \(BC\) thì \(D\) di chuyển trên cung \(CE\) thuộc cung chứa góc \(30^0\) dựng trên \(BC.\)


Bình chọn:
4.4 trên 8 phiếu
Bài tiếp theo
  • Bài 14 trang 135 SGK Toán 9 tập 2

    Giải bài 14 trang 135 SGK Toán 9 tập 2. Dựng tam giác ABC, biết BC = 4cm, góc A = 60o, bán kính đường tròn nội tiếp tam giác bằng 1cm.

  • Bài 15 trang 135 SGK Toán 9 tập 2

    Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E.

  • Bài 16 trang 135 SGK Toán 9 tập 2

    Một mặt phẳng chứa trụ OO' của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài 3cm, chiều rộng 2cm.Tính diện tích xung quanh và thể tích hình trụ đó.

  • Bài 17 trang 135 SGK Toán 9 tập 2

    Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc ACB = 30o. Tính diện tích xung quanh và thể tích hình nón.

  • Bài 18 trang 135 SGK Toán 9 tập 2

    Giải bài 18 trang 135 SGK Toán 9 tập 2. Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3).

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store