 Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
 Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
Bài tập 12 trang 157 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho tam giác MNP có MN = MP. Gọi E là trung điểm của MN, F là trung điểm của MP. Gọi I là giao điểm của NF và PE. Chứng minh rằng:
Đề bài
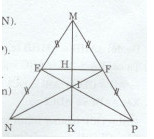
Cho tam giác MNP có MN = MP. Gọi E là trung điểm của MN, F là trung điểm của MP. Gọi I là giao điểm của NF và PE. Chứng minh rằng:
a) \(\Delta MEP = \Delta MFN\)
b) \(\Delta IEN = \Delta IFP\)
c) MI là phân giác của góc NMP.
d) EF // NP.
Lời giải chi tiết
a)Ta có: \(ME = NE = {{MN} \over 2}\) (F là trung điểm của MN)
\(MF = PF = {{MP} \over 2}\) (F là trung điểm của NP)
Mà MN = MP (giả thiết) nên ME = NE = MF = PF.
Xét tam giác MEP và MFN có:
ME = MF (chứng minh trên)
\(\widehat {EMP}\) là góc chung
MP = MN (giả thiết)
Do đó: \(\Delta MEP = \Delta MFN(c.g.c)\)
b)Ta có: \(\Delta MEP = \Delta MFN\) (chứng minh câu a) \( \Rightarrow \widehat {MEP} = \widehat {MFN};\widehat {MPE} = \widehat {MNF}\)
\(\widehat {MEP} + \widehat {NEP} = \widehat {MFN} + \widehat {NFP}( = {180^0})\)
Mà \(\widehat {MEP} = \widehat {MFN}\) (chứng minh trên) do đó: \(\widehat {NEP} = \widehat {NFP}.\)
Xét tam giác IEN và IFP có:
\(\widehat {IEN} = \widehat {IFP}\) (chứng minh trên)
EN = EP (chứng minh câu a)
\(\widehat {ENI} = \widehat {FPI}(\Delta MEP = \Delta MFN)\)
Do đó: \(\Delta IEN = \Delta IFP(g.c.g)\)
c) Xét tam giác MIN và MIP có:
MI là cạnh chung
MN = MP (giả thiết)
NI = PI \((\Delta IEN = \Delta IFP)\)
Do đó: \(\Delta MIN = \Delta MIP(c.c.c) \Rightarrow \widehat {IMN} = \widehat {IMP}\)
Vậy MI là tia phân giác của góc NMP.
d) Gọi H, K lần lượt là giao điểm của MI với EF, NP.
Xét tam giác MHE và MHF có:
ME = MF
\(\widehat {HME} = \widehat {HMF}\) (chứng minh trên)
MH là cạnh chung.
Do đó: \(\Delta MHE = \Delta MHF(c.g.c) \Rightarrow \widehat {MHE} = \widehat {MHF}\)
Mà \(\widehat {MHE} + \widehat {MHF} = {180^0}\) (kề bù) nên \(\widehat {MHE} + \widehat {MHE} = {180^0}\)
\( \Rightarrow 2\widehat {MHE} = {180^0} \Rightarrow \widehat {MHE} = {90^0} \Rightarrow MH \bot EFhayMK \bot EF\)
Xét tam giác MKN và MKP có:
MN = MP (gt)
\(\widehat {KMN} = \widehat {KMP}(cmt)\)
Mk là cạnh chung.
Do đó: \(\Delta MKN = \Delta MKP(c.g.c) \Rightarrow \widehat {MKN} = \widehat {MKP}\)
Mà \(\widehat {MKN} + \widehat {MKP} = {180^0}\) (kề bù) nên \(\widehat {MKN} + \widehat {MKN} = {180^0}.\)
\( \Rightarrow 2\widehat {MKN} = {180^0} \Rightarrow \widehat {MKN} = {90^0} \Rightarrow MK \bot NP\)
Ta có: \(EF \bot MK;NP \bot MK.\) Vậy EF // NP.
Loigiaihya.com
Các bài khác cùng chuyên mục












Danh sách bình luận