Trắc nghiệm Bài 3: Tính chất đường phân giác của tam giác Toán 8 Chân trời sáng tạo
Đề bài
Trong tam giác, đường… chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Từ (cụm từ) thích hợp điền vào dấu … để được đáp án đúng là
-
A.
cao
-
B.
phân giác của một góc
-
C.
trung tuyến
-
D.
trung trực
Cho tam giác ABC có AD là phân giác trong của góc A. Khi đó,
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}\)
-
B.
\(\frac{{DC}}{{AC}} = \frac{{AB}}{{DB}}\)
-
C.
\(\frac{{AB}}{{BD}} = \frac{{DC}}{{AC}}\)
-
D.
\(\frac{{DC}}{{BD}} = \frac{{AC}}{{AB}}\)
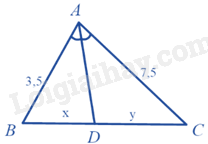
-
A.
\(\frac{x}{y} = \frac{7}{{15}}\)
-
B.
\(\frac{x}{y} = \frac{8}{{15}}\)
-
C.
\(\frac{x}{y} = \frac{{11}}{{15}}\)
-
D.
\(\frac{x}{y} = \frac{4}{{15}}\)
Cho tam giác ABC có AD là đường phân giác của tam giác. Biết rằng \(BD = 3cm,DC = 4cm.\) Khi đó, tỉ số \(\frac{{AB}}{{AC}}\) bằng:
-
A.
\(\frac{4}{5}\)
-
B.
\(\frac{5}{4}\)
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{4}{3}\)
Đáp án nào dưới đây có tỉ số \(\frac{{BD}}{{DC}} = \frac{3}{4}\) ?
-
A.
-
B.
-
C.
-
D.
Không có đáp án nào đúng
Cho tam giác ABC có \(AB < AC,\) AD là đường phân giác. Khi đó:
-
A.
\(BD < DC\)
-
B.
\(BD > DC\)
-
C.
\(BD = DC\)
-
D.
Không so sánh được
-
A.
\(x = 12\)
-
B.
\(x = \frac{{34}}{5}\)
-
C.
\(x = \frac{{37}}{5}\)
-
D.
\(x = \frac{{36}}{5}\)
-
A.
\(BD = \frac{3}{4}DC\)
-
B.
\(BD = \frac{2}{3}DC\)
-
C.
\(BD = \frac{1}{3}DC\)
-
D.
\(BD = \frac{1}{2}DC\)
-
A.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{5}{6}\)
-
B.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{4}{5}\)
-
C.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{2}{3}\)
-
D.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{3}{4}\)
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E.
Chọn đáp án đúng.
-
A.
\(\frac{{EC}}{{EA}} = \frac{1}{3}.\frac{{DM}}{{DA}}\)
-
B.
\(\frac{{EC}}{{EA}} = 3\frac{{DM}}{{DA}}\)
-
C.
\(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\)
-
D.
\(\frac{{EC}}{{EA}} = \frac{1}{2}.\frac{{DM}}{{DA}}\)
Cho tam giác ABC vuông tại A có \(AB = 4cm,BC = 5cm.\) Vẽ AD là phân giác của góc BAC. Tỉ số \(\frac{{DB}}{{DC}}\) là:
-
A.
2
-
B.
\(\frac{5}{3}\)
-
C.
\(\frac{4}{3}\)
-
D.
\(\frac{3}{2}\)
Cho tam giác ABC có \(BC = 10cm.\) Vẽ AD là tia phân giác của góc BAC sao cho \(BD = 4cm.\) Tỉ số \(\frac{{AB}}{{AC}}\) là:
-
A.
\(\frac{4}{5}\)
-
B.
\(\frac{7}{8}\)
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{2}{3}\)
Cho tam giác ABC vuông tại A, có \(AB = 3cm,AC = 4cm,AD\) là đường phân giác. Khoảng cách từ điểm D đến đường thẳng AC là:
-
A.
\(\frac{{12}}{{49}}cm\)
-
B.
\(\frac{{12}}{7}cm\)
-
C.
\(\frac{{13}}{7}cm\)
-
D.
\(\frac{{13}}{{49}}cm\)
-
A.
\(\frac{8}{3}\)
-
B.
3
-
C.
\(\frac{{10}}{3}\)
-
D.
Đáp án khác
: Cho tam giác ABC vuông tại A có \(AB = 15cm,AC = 20cm\) , đường cao AH (H thuộc BC). Tia phân giác của góc HAB cắt HB tại D. Tia phân giác của góc HAC cắt HC tại E. Độ dài đoạn thẳng DH bằng:
-
A.
4cm
-
B.
6cm
-
C.
9cm
-
D.
12cm
Cho tam giác ABC cân tại A, đường phân giác của góc ABC cắt AC tại D và \(AB = 15cm,BC = 10cm.\) Khi đó, độ dài đoạn thẳng AD bằng
-
A.
3cm
-
B.
6cm
-
C.
9cm
-
D.
12cm
Cho tam giác ABC có chu vi 27cm, các đường phân giác BD và CE. Biết rằng \(\frac{{AD}}{{DC}} = \frac{1}{2},\frac{{AE}}{{EB}} = \frac{3}{4}\) . Chọn đáp án đúng.
-
A.
\(AB = 12cm,BC = 9cm,AC = 6cm\)
-
B.
\(AB = 6cm,BC = 12cm,AC = 9cm\)
-
C.
\(AB = 6cm,BC = 9cm,AC = 12cm\)
-
D.
\(AB = 12cm,BC = 6cm,AC = 9cm\)
: Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Biết rằng \(AB = m,AC = n\left( {n > m} \right)\) . Diện tích tam giác ADM là:
-
A.
\({S_{AMD}} = \frac{{n + m}}{{3\left( {m - n} \right)}}S{ _{ABC}}\)
-
B.
\({S_{AMD}} = \frac{{n - m}}{{3\left( {m + n} \right)}}S{ _{ABC}}\)
-
C.
\({S_{AMD}} = \frac{{n + m}}{{2\left( {m - n} \right)}}S{ _{ABC}}\)
-
D.
\({S_{AMD}} = \frac{{n - m}}{{2\left( {m + n} \right)}}S{ _{ABC}}\)
Cho hình bình hành ABCD có \(AB = a = 12,5cm,BC = b = 7,25cm.\) Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F. Biết rằng \(FE = m = 3,45cm\) .
Chọn đáp án đúng
-
A.
\(AC \approx 12,98cm\)
-
B.
\(AC \approx 12,97cm\)
-
C.
\(AC \approx 12,88cm\)
-
D.
\(AC \approx 12,87cm\)
Cho tam giác ABC có \(AB = 4cm,AC = 5cm,BC = 6cm\) , các đường phân giác BD, CE cắt nhau tại I. Tỉ số diện tích của các tam giác ADE và ABC là:
-
A.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{3}{{11}}\)
-
B.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{2}{{11}}\)
-
C.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{4}{{11}}\)
-
D.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{5}{{11}}\)
Cho tam giác ABC có \(AB = 8cm,AC = 12cm,\) đường phân giác AD. Trên đoạn AD lấy điểm E sao cho \(\frac{{AE}}{{AD}} = \frac{3}{5}.\) Gọi K là giao điểm của BE và AC. Tính tỉ số \(\frac{{AK}}{{KC}}\)
-
A.
\(\frac{3}{5}\)
-
B.
\(\frac{3}{4}\)
-
C.
\(\frac{3}{7}\)
-
D.
\(\frac{4}{7}\)
Cho tam giác ABC có \(AB = c,AC = b,BC = a,\) các đường phân giác AD, BE, CF cắt nhau ở I. Chọn đáp án đúng
-
A.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = \frac{1}{2}\)
-
B.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = 2\)
-
C.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = 1\)
-
D.
Đáp án khác
-
A.
\(x = 13\)
-
B.
\(x = 12\)
-
C.
\(x = 14\)
-
D.
Cả A, B, C đều sai
Cho tam giác ABC có \(AB = 2,BC = 3,CA = 4\) , AD là đường phân giác và I là giao điểm của ba đường phân giác của tam giác đó. Tính tỉ số \(\frac{{ID}}{{IA}}\)
-
A.
\(\frac{5}{6}\)
-
B.
\(\frac{1}{3}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{3}{4}\)
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Khi đó:
-
A.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{1}{2}\)
-
B.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)
-
C.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 2\)
-
D.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{1}{3}\)
Cho tam giác ABC có AM là đường trung tuyến. Gọi MD, ME lần lượt là đường phân giác của các tam giác AMB và AMC. Gọi I là giao điểm của DE và AM.
Chọn đáp án đúng.
-
A.
\(DI = \frac{4}{5}IE\)
-
B.
\(DI = \frac{3}{4}IE\)
-
C.
\(DI = \frac{2}{3}IE\)
-
D.
\(DI = IE\)
Cho tam giác ABC có \(BA = BC = a,AC = b.\) Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Tính MN
-
A.
\(MN = \frac{{2ab}}{{a + b}}\)
-
B.
\(MN = \frac{{ab}}{{a + b}}\)
-
C.
\(MN = \frac{{ab}}{{2\left( {a + b} \right)}}\)
-
D.
\(MN = \frac{{ab}}{{a + b}}\)
Lời giải và đáp án
Trong tam giác, đường… chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Từ (cụm từ) thích hợp điền vào dấu … để được đáp án đúng là
-
A.
cao
-
B.
phân giác của một góc
-
C.
trung tuyến
-
D.
trung trực
Đáp án : B
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Cho tam giác ABC có AD là phân giác trong của góc A. Khi đó,
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}\)
-
B.
\(\frac{{DC}}{{AC}} = \frac{{AB}}{{DB}}\)
-
C.
\(\frac{{AB}}{{BD}} = \frac{{DC}}{{AC}}\)
-
D.
\(\frac{{DC}}{{BD}} = \frac{{AC}}{{AB}}\)
Đáp án : D
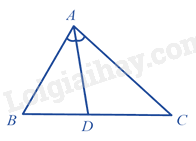
Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{DC}}{{BD}} = \frac{{AC}}{{AB}}\) (tính chất đường phân giác)
-
A.
\(\frac{x}{y} = \frac{7}{{15}}\)
-
B.
\(\frac{x}{y} = \frac{8}{{15}}\)
-
C.
\(\frac{x}{y} = \frac{{11}}{{15}}\)
-
D.
\(\frac{x}{y} = \frac{4}{{15}}\)
Đáp án : A
Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\) , do đó \(\frac{x}{y} = \frac{{3,5}}{{7,5}} = \frac{7}{{15}}\)
Cho tam giác ABC có AD là đường phân giác của tam giác. Biết rằng \(BD = 3cm,DC = 4cm.\) Khi đó, tỉ số \(\frac{{AB}}{{AC}}\) bằng:
-
A.
\(\frac{4}{5}\)
-
B.
\(\frac{5}{4}\)
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{4}{3}\)
Đáp án : C
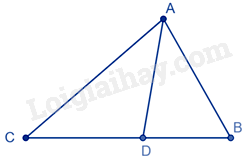
Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}} = \frac{3}{4}\)
Đáp án nào dưới đây có tỉ số \(\frac{{BD}}{{DC}} = \frac{3}{4}\) ?
-
A.
-
B.
-
C.
-
D.
Không có đáp án nào đúng
Đáp án : A
Đáp án A: Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}} = \frac{3}{4}\)
Đáp án B, C không đúng.
Cho tam giác ABC có \(AB < AC,\) AD là đường phân giác. Khi đó:
-
A.
\(BD < DC\)
-
B.
\(BD > DC\)
-
C.
\(BD = DC\)
-
D.
Không so sánh được
Đáp án : A
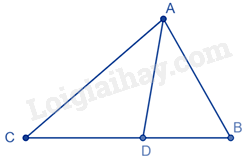
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\)
Mà \(AB < AC\) nên \(\frac{{AB}}{{AC}} < 1\) do đó \(\frac{{BD}}{{DC}} < 1\) nên \(BD < DC\)
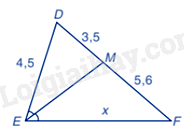
-
A.
\(x = 12\)
-
B.
\(x = \frac{{34}}{5}\)
-
C.
\(x = \frac{{37}}{5}\)
-
D.
\(x = \frac{{36}}{5}\)
Đáp án : D
Xét tam giác EDF có EM là tia phân giác của góc FED nên \(\frac{{DM}}{{MF}} = \frac{{ED}}{{FE}}\) hay \(\frac{{3,5}}{{5,6}} = \frac{{4,5}}{x}\)
\(x = \frac{{4,5.5,6}}{{3,5}} = \frac{{36}}{5}\)
-
A.
\(BD = \frac{3}{4}DC\)
-
B.
\(BD = \frac{2}{3}DC\)
-
C.
\(BD = \frac{1}{3}DC\)
-
D.
\(BD = \frac{1}{2}DC\)
Đáp án : D
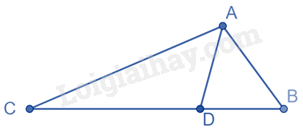
Vì \(AC = 2AB\) nên \(\frac{{AC}}{{AB}} = 2\)
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{DC}}{{BD}} = \frac{{AC}}{{AB}} = 2\) nên \(BD = \frac{1}{2}DC\)
-
A.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{5}{6}\)
-
B.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{4}{5}\)
-
C.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{2}{3}\)
-
D.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{3}{4}\)
Đáp án : D
Vì hai tam giác ADC và ADB có cùng đường cao xuất phát từ đỉnh A xuống BC.
Do đó, \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{{BD}}{{DC}}\)
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{15}}{{20}} = \frac{3}{4}\)
Vậy \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{3}{4}\)
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E.
Chọn đáp án đúng.
-
A.
\(\frac{{EC}}{{EA}} = \frac{1}{3}.\frac{{DM}}{{DA}}\)
-
B.
\(\frac{{EC}}{{EA}} = 3\frac{{DM}}{{DA}}\)
-
C.
\(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\)
-
D.
\(\frac{{EC}}{{EA}} = \frac{1}{2}.\frac{{DM}}{{DA}}\)
Đáp án : C
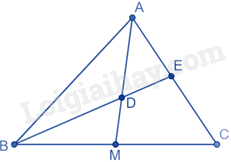
Xét tam giác ABC có BE là đường phân giác của góc ABC nên \(\frac{{EC}}{{EA}} = \frac{{BC}}{{BA}}\) (1)
Xét tam giác ABM có DB là đường phân giác của góc ABM nên \(\frac{{DM}}{{DA}} = \frac{{BM}}{{BA}}\) (2)
Mà M là trung điểm của BC nên \(BM = MC = \frac{1}{2}BC \Rightarrow \frac{{DM}}{{DA}} = \frac{{BM}}{{BA}} = \frac{{BC}}{{2.BA}}\)
Nên \(2\frac{{DM}}{{DA}} = \frac{{BC}}{{BA}}\) (3)
Từ (1), (2) và (3) ta có: \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\) .
Cho tam giác ABC vuông tại A có \(AB = 4cm,BC = 5cm.\) Vẽ AD là phân giác của góc BAC. Tỉ số \(\frac{{DB}}{{DC}}\) là:
-
A.
2
-
B.
\(\frac{5}{3}\)
-
C.
\(\frac{4}{3}\)
-
D.
\(\frac{3}{2}\)
Đáp án : C
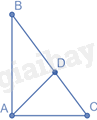
Áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có: \(A{B^2} + A{C^2} = B{C^2}\)
\(A{C^2} = B{C^2} - A{B^2} = 16\) nên \(AC = 3cm\)
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{4}{3}\)
Cho tam giác ABC có \(BC = 10cm.\) Vẽ AD là tia phân giác của góc BAC sao cho \(BD = 4cm.\) Tỉ số \(\frac{{AB}}{{AC}}\) là:
-
A.
\(\frac{4}{5}\)
-
B.
\(\frac{7}{8}\)
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{2}{3}\)
Đáp án : D
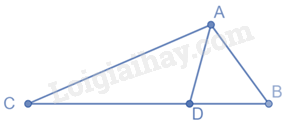
Ta có: \(CD = BC - CD = 6cm\)
Tam giác ABC có AD là phân giác của góc BAC nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{4}{6} = \frac{2}{3}\)
Cho tam giác ABC vuông tại A, có \(AB = 3cm,AC = 4cm,AD\) là đường phân giác. Khoảng cách từ điểm D đến đường thẳng AC là:
-
A.
\(\frac{{12}}{{49}}cm\)
-
B.
\(\frac{{12}}{7}cm\)
-
C.
\(\frac{{13}}{7}cm\)
-
D.
\(\frac{{13}}{{49}}cm\)
Đáp án : B
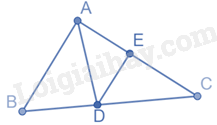
Kẻ DE vuông góc với AC tại E, khi đó DE là khoảng cách từ D đến AC
Lại có: AB vuông góc với AC nên DE//AB
Áp dụng định lý Pytago vào tam giác ABC vuông tại A có: \(B{C^2} = A{B^2} + A{C^2} = 25\) nên \(BC = 5cm\)
Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{3}{4}\) nên \(BD = \frac{3}{4}DC\)
Ta có: \(BD + DC = BC\)
\(\frac{3}{4}DC + DC = 5\) nên \(DC = \frac{{20}}{7}cm\)
Tam giác ABC có DE//AB nên theo hệ quả của định lý Thalès ta có:
\(\frac{{DE}}{{AB}} = \frac{{DC}}{{BC}}\) hay \(\frac{{DE}}{3} = \frac{{\frac{{20}}{7}}}{5} = \frac{4}{7}\) nên \(DE = \frac{4}{7}.3 = \frac{{12}}{7}\left( {cm} \right)\)
Vì AD là đường phân giác của góc BAC nên \(\widehat {DAE} = \frac{1}{2}\widehat {BAC} = {45^0}\)
Mà tam giác DAE vuông tại E nên tam giác DAE vuông cân tại E. Do đó, \(DE = AE = \frac{{12}}{7}cm\)
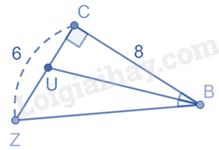
-
A.
\(\frac{8}{3}\)
-
B.
3
-
C.
\(\frac{{10}}{3}\)
-
D.
Đáp án khác
Đáp án : A
Tam giác BCZ vuông tại C nên theo định lý Pytago ta có:
\(BZ = \sqrt {B{C^2} + C{Z^2}} = 10\)
Trong tam giác BCZ có BU là đường phân giác của góc CBZ nên \(\frac{{UC}}{{UZ}} = \frac{{BC}}{{BZ}} = \frac{8}{{10}} = \frac{4}{5}\)
Do đó, \(\frac{{UC}}{4} = \frac{{UZ}}{5}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{UC}}{4} = \frac{{UZ}}{5} = \frac{{UC + UZ}}{{4 + 5}} = \frac{{CZ}}{9} = \frac{6}{9} = \frac{2}{3}\) nên \(UC = 4.\frac{2}{3} = \frac{8}{3}\)
: Cho tam giác ABC vuông tại A có \(AB = 15cm,AC = 20cm\) , đường cao AH (H thuộc BC). Tia phân giác của góc HAB cắt HB tại D. Tia phân giác của góc HAC cắt HC tại E. Độ dài đoạn thẳng DH bằng:
-
A.
4cm
-
B.
6cm
-
C.
9cm
-
D.
12cm
Đáp án : A
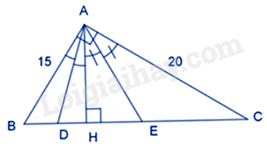
Áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có: \(B{C^2} = A{B^2} + A{C^2} = 625\) nên \(BC = 25cm\)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\) nên \(AH = \frac{{AB.AC}}{{BC}} = \frac{{15.20}}{{25}} = 12\left( {cm} \right)\)
Áp dụng định lý Pytago vào tam giác AHB vuông tại H có: \(A{B^2} = A{H^2} + H{B^2}\)
\(H{B^2} = A{B^2} - A{H^2} = 81\) nên \(HB = 9cm\) , do đó, \(HC = BC - HB = 16\left( {cm} \right)\)
Vì AD là đường phân giác của góc BAH trong tam giác ABH nên
\(\frac{{AB}}{{AH}} = \frac{{BD}}{{DH}} = \frac{{BH - DH}}{{DH}}\) nên \(\frac{{15}}{{12}} = \frac{{9 - DH}}{{DH}}\)
\(15DH = 108 - 12DH\) nên \(DH = 4cm\)
Cho tam giác ABC cân tại A, đường phân giác của góc ABC cắt AC tại D và \(AB = 15cm,BC = 10cm.\) Khi đó, độ dài đoạn thẳng AD bằng
-
A.
3cm
-
B.
6cm
-
C.
9cm
-
D.
12cm
Đáp án : C
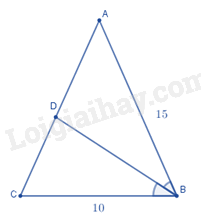
Vì tam giác ABC cân tại A nên \(AB = AC = 15cm\)
Xét tam giác ABC có BD là đường phân giác của góc ABC nên \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}}\) , do đó \(\frac{{AD}}{{AD + DC}} = \frac{{AB}}{{BC + AB}}\) hay \(\frac{{AD}}{{AC}} = \frac{{AB}}{{BC + AB}}\) , do đó \(\frac{{AD}}{{15}} = \frac{{15}}{{15 + 10}}\)
Suy ra: \(AD = \frac{{15.15}}{{25}} = 9\left( {cm} \right)\)
Cho tam giác ABC có chu vi 27cm, các đường phân giác BD và CE. Biết rằng \(\frac{{AD}}{{DC}} = \frac{1}{2},\frac{{AE}}{{EB}} = \frac{3}{4}\) . Chọn đáp án đúng.
-
A.
\(AB = 12cm,BC = 9cm,AC = 6cm\)
-
B.
\(AB = 6cm,BC = 12cm,AC = 9cm\)
-
C.
\(AB = 6cm,BC = 9cm,AC = 12cm\)
-
D.
\(AB = 12cm,BC = 6cm,AC = 9cm\)
Đáp án : B
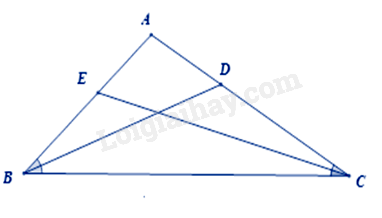
Vì BD, CE là các đường phân giác trong tam giác ABC nên:
\(\frac{{AB}}{{BC}} = \frac{{AD}}{{DC}} = \frac{1}{2};\frac{{AC}}{{BC}} = \frac{{AE}}{{EB}} = \frac{3}{4}\)
Do đó \(\frac{{AB}}{2} = \frac{{BC}}{4} = \frac{{AC}}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AB}}{2} = \frac{{BC}}{4} = \frac{{AC}}{3} = \frac{{AB + BC + AC}}{{2 + 4 + 3}} = \frac{{27}}{9} = 3\)
Do đó, \(AB = 6cm,BC = 12cm,AC = 9cm\)
: Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Biết rằng \(AB = m,AC = n\left( {n > m} \right)\) . Diện tích tam giác ADM là:
-
A.
\({S_{AMD}} = \frac{{n + m}}{{3\left( {m - n} \right)}}S{ _{ABC}}\)
-
B.
\({S_{AMD}} = \frac{{n - m}}{{3\left( {m + n} \right)}}S{ _{ABC}}\)
-
C.
\({S_{AMD}} = \frac{{n + m}}{{2\left( {m - n} \right)}}S{ _{ABC}}\)
-
D.
\({S_{AMD}} = \frac{{n - m}}{{2\left( {m + n} \right)}}S{ _{ABC}}\)
Đáp án : D
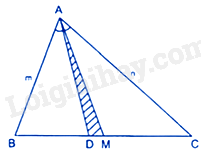
Vì tam giác ADM và tam giác ABC có chung chiều cao kẻ từ A đến BC nên \(\frac{{{S_{ADM}}}}{{{S_{ABC}}}} = \frac{{DM}}{{BC}} \Rightarrow {S_{ADM}} = \frac{{DM}}{{BC}}.{S_{ABC}}\)
Xét tam giác ABC có AD là đường phân giác của góc BAC nên: \(\frac{{DB}}{{DC}} = \frac{{BA}}{{CA}} = \frac{m}{n} \Rightarrow DB = mt,DC = nt\) (với \(t > 0\) )
Do đó, \(BC = DC + BD = \left( {m + n} \right)t\) , suy ra \(BM = \frac{1}{2}BC = \frac{{\left( {m + n} \right)t}}{2}\)
Ta có: \(DM = BM - DB = \frac{{\left( {m + n} \right)t - 2mt}}{2} = \frac{{\left( {n - m} \right)t}}{2}\)
Suy ra: \(\frac{{DM}}{{BC}} = \frac{{\frac{{\left( {n - m} \right)t}}{2}}}{{\left( {m + n} \right)t}} = \frac{{n - m}}{{2\left( {m + n} \right)}}\)
Vậy \({S_{AMD}} = \frac{{n - m}}{{2\left( {m + n} \right)}}S{ _{ABC}}\)
Cho hình bình hành ABCD có \(AB = a = 12,5cm,BC = b = 7,25cm.\) Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F. Biết rằng \(FE = m = 3,45cm\) .
Chọn đáp án đúng
-
A.
\(AC \approx 12,98cm\)
-
B.
\(AC \approx 12,97cm\)
-
C.
\(AC \approx 12,88cm\)
-
D.
\(AC \approx 12,87cm\)
Đáp án : A
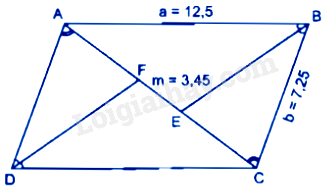
Vì ABCD là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}.\)
Vì BE và DF lần lượt là phân giác của góc ABC và góc ADC nên \(\widehat {ADF} = \widehat {CBE}\)
Mặt khác, ta có: \(AD = CB = b,\widehat {DAF} = \widehat {BCE}\) (so le trong)
Suy ra: \(\Delta ADF = \Delta CBE\left( {g.c.g} \right)\) nên \(AF = CE\)
Đặt \(AF = CE = x\)
Xét tam giác ABC có BE là đường phân giác của góc ABC nên
\(\frac{{AB}}{{BC}} = \frac{{AE}}{{CE}} = \frac{{FA + FE}}{{CE}} \Rightarrow \frac{a}{b} = \frac{{x + m}}{x} \Rightarrow x = \frac{{mb}}{{a - b}}\)
\(AC = 2x + m = \frac{{2mb}}{{a - b}} + m = \frac{{m\left( {a + b} \right)}}{{a - b}} = \frac{{3,45\left( {12,5 + 7,25} \right)}}{{12,5 - 7,25}} \approx 12,98cm\)
Cho tam giác ABC có \(AB = 4cm,AC = 5cm,BC = 6cm\) , các đường phân giác BD, CE cắt nhau tại I. Tỉ số diện tích của các tam giác ADE và ABC là:
-
A.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{3}{{11}}\)
-
B.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{2}{{11}}\)
-
C.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{4}{{11}}\)
-
D.
\(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{5}{{11}}\)
Đáp án : B
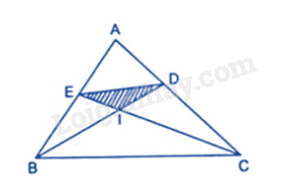
Tam giác ABC có BD là đường phân giác của góc ABC nên \(\frac{{DA}}{{DC}} = \frac{{AB}}{{BC}} = \frac{4}{6} = \frac{2}{3} \Rightarrow AD = \frac{2}{3}DC\)
Lại có: \(AC = DC + AD = \frac{2}{3}DC + DC = \frac{5}{3}DC \Rightarrow \frac{5}{3}DC = 5 \Rightarrow DC = 3cm \Rightarrow AD = 2cm\)
Vì tam giác DAE và tam giác CAE có chung đường cao kẻ từ E đến AC nên \(\frac{{{S_{DAE}}}}{{{S_{ACE}}}} = \frac{{AD}}{{AC}} = \frac{2}{5}\left( 1 \right)\)
Vì tam giác ACE và tam giác CAB có chung đường cao kẻ từ C đến AB nên \(\frac{{{S_{ACE}}}}{{{S_{ABC}}}} = \frac{{AE}}{{AB}}\left( 2 \right)\)
Tam giác ABC có CE là đường phân giác của góc ACB nên:
\(\frac{{AE}}{{EB}} = \frac{{AC}}{{BC}} \Rightarrow \frac{{AE}}{{AC}} = \frac{{EB}}{{BC}}\) hay \(\frac{{AE}}{5} = \frac{{EB}}{6}\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AE}}{5} = \frac{{EB}}{6} = \frac{{AE + EB}}{{5 + 6}} = \frac{{AB}}{{11}} = \frac{4}{{11}}\)
Suy ra: \(AE = \frac{4}{{11}}.5 = \frac{{20}}{{11}} \Rightarrow \frac{{AE}}{{AB}} = \frac{5}{{11}}\left( 3 \right)\)
Thay (3) vào (2) ta có: \(\frac{{{S_{ACE}}}}{{{S_{ABC}}}} = \frac{5}{{11}}\left( 4 \right)\)
Nhân vế với vế của (1) và (4) ta có: \(\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{2}{5}.\frac{5}{{11}} = \frac{2}{{11}}\)
Cho tam giác ABC có \(AB = 8cm,AC = 12cm,\) đường phân giác AD. Trên đoạn AD lấy điểm E sao cho \(\frac{{AE}}{{AD}} = \frac{3}{5}.\) Gọi K là giao điểm của BE và AC. Tính tỉ số \(\frac{{AK}}{{KC}}\)
-
A.
\(\frac{3}{5}\)
-
B.
\(\frac{3}{4}\)
-
C.
\(\frac{3}{7}\)
-
D.
\(\frac{4}{7}\)
Đáp án : A
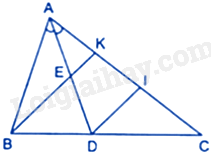
Kẻ DI//BK thì DI//EK
Áp dụng định lý Thalès vào tam giác AID và tam giác BKC ta được: \(\frac{{AK}}{{KI}} = \frac{{AE}}{{ED}} = \frac{3}{2}\) \( \Rightarrow AK = \frac{{3KI}}{2}\left( 1 \right);\frac{{CK}}{{KI}} = \frac{{CB}}{{BD}}\left( 2 \right)\)
Tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{DC}}{{DB}} = \frac{{CA}}{{AB}}\) hay \(\frac{{CD}}{{DB}} = \frac{{12}}{8} = \frac{3}{2} \Rightarrow \frac{{CD}}{3} = \frac{{DB}}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{CD}}{3} = \frac{{DB}}{2} = \frac{{CD + DB}}{{2 + 3}} = \frac{{BC}}{5} \Rightarrow \frac{{CB}}{{DB}} = \frac{5}{2}\left( 3 \right)\)
Thay (3) vào (2) ta có: \(\frac{{CK}}{{KI}} = \frac{5}{2} \Rightarrow CK = \frac{5}{2}KI\left( 4 \right)\)
Chia theo vế các đẳng thức của (1) và (4) ta được: \(\frac{{AK}}{{KC}} = \frac{{3KI}}{2}:\frac{{5KI}}{2} = \frac{3}{5}\)
Cho tam giác ABC có \(AB = c,AC = b,BC = a,\) các đường phân giác AD, BE, CF cắt nhau ở I. Chọn đáp án đúng
-
A.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = \frac{1}{2}\)
-
B.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = 2\)
-
C.
\(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = 1\)
-
D.
Đáp án khác
Đáp án : C
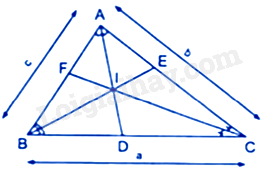
Áp dụng tính chất của đường phân giác AD và BI vào các tam giác ABC, ABD ta được: \(\frac{{DI}}{{IA}} = \frac{{DB}}{{BA}} = \frac{{DB}}{c}\left( 1 \right)\)
\(\frac{{DB}}{{BA}} = \frac{{DC}}{{CA}}\) hay \(\frac{{DB}}{c} = \frac{{DC}}{b}\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{DB}}{c} = \frac{{DC}}{b} = \frac{{DB + DC}}{{c + b}} = \frac{{BC}}{{b + c}} \Rightarrow DB = \frac{{ca}}{{b + c}}\left( 2 \right)\)
Thay (2) vào (1) ta được: \(\frac{{DI}}{{IA}} = \frac{{ca}}{{c\left( {b + c} \right)}} = \frac{a}{{b + c}}\)
Suy ra: \(\frac{{DI}}{a} = \frac{{IA}}{{b + c}} = \frac{{DI + IA}}{{a + b + c}} = \frac{{AD}}{{a + b + c}} \Rightarrow \frac{{DI}}{{AD}} = \frac{a}{{a + b + c}}\left( 3 \right)\)
Chứng minh tương tự ta có: \(\frac{{EI}}{{EB}} = \frac{b}{{a + b + c}},\frac{{FI}}{{FC}} = \frac{c}{{a + b + c}}\left( 5 \right)\)
Cộng theo vế của (3), (4), (5) ta có: \(\frac{{DI}}{{DA}} + \frac{{EI}}{{EB}} + \frac{{FI}}{{FC}} = \frac{{a + b + c}}{{a + b + c}} = 1\)
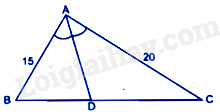
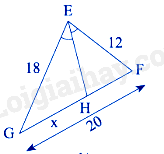
-
A.
\(x = 13\)
-
B.
\(x = 12\)
-
C.
\(x = 14\)
-
D.
Cả A, B, C đều sai
Đáp án : B
Ta có: \(HF = GF - GH = 20 - x\)
Xét tam giác GEF có EH là đường phân giác của góc GEF nên
\(\frac{{GH}}{{HF}} = \frac{{EG}}{{FE}}\) hay \(\frac{x}{{20 - x}} = \frac{{18}}{{12}}\)
\(12x = 18\left( {20 - x} \right)\)
\(12x = 360 - 18x\)
\(30x = 360\)
\(x = 12\)
Cho tam giác ABC có \(AB = 2,BC = 3,CA = 4\) , AD là đường phân giác và I là giao điểm của ba đường phân giác của tam giác đó. Tính tỉ số \(\frac{{ID}}{{IA}}\)
-
A.
\(\frac{5}{6}\)
-
B.
\(\frac{1}{3}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{3}{4}\)
Đáp án : C
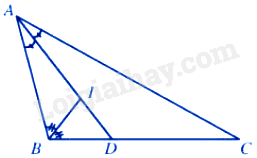
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{2}{4} = \frac{1}{2}\) nên \(\frac{{DB}}{1} = \frac{{DC}}{2}\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{DB}}{1} = \frac{{DC}}{2} = \frac{{DB + DC}}{{1 + 2}} = \frac{{BC}}{3} = \frac{3}{3} = 1\)
Do đó, \(DB = 1\)
Xét tam giác ABD có BI là đường phân giác của góc ABD nên \(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{1}{2}\)
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Khi đó:
-
A.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{1}{2}\)
-
B.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)
-
C.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 2\)
-
D.
\(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{1}{3}\)
Đáp án : B
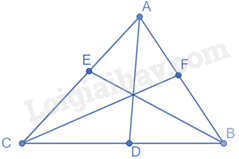
Xét tam giác ABC có:
AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
BE là đường phân giác của góc ABC nên \(\frac{{EC}}{{EA}} = \frac{{BC}}{{AB}}\)
CF là đường phân giác của góc BCA nên \(\frac{{FA}}{{FB}} = \frac{{AC}}{{BC}}\)
Do đó, \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{AB}}.\frac{{AC}}{{BC}} = 1\)
Cho tam giác ABC có AM là đường trung tuyến. Gọi MD, ME lần lượt là đường phân giác của các tam giác AMB và AMC. Gọi I là giao điểm của DE và AM.
Chọn đáp án đúng.
-
A.
\(DI = \frac{4}{5}IE\)
-
B.
\(DI = \frac{3}{4}IE\)
-
C.
\(DI = \frac{2}{3}IE\)
-
D.
\(DI = IE\)
Đáp án : D
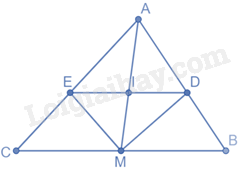
Xét tam giác AMB có MD là đường phân giác của góc AMB nên \(\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\)
Xét tam giác AMC có ME là đường phân giác của góc AMC nên \(\frac{{EA}}{{EC}} = \frac{{MA}}{{MC}}\)
Mà \(MB = MC\) nên \(\frac{{MA}}{{AB}} = \frac{{MA}}{{MC}}\) nên \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\) , do đó DE//BC (định lý Thalès đảo)
Áp dụng hệ quả của định lý Thalès vào hai tam giác ABM và ACM có:
\(\frac{{ID}}{{MB}} = \frac{{IA}}{{AM}}\) và \(\frac{{IE}}{{MC}} = \frac{{AI}}{{AM}}\) , do đó, \(\frac{{ID}}{{MB}} = \frac{{IE}}{{MC}}\)
Mà \(MB = MC\) nên \(DI = IE\)
Cho tam giác ABC có \(BA = BC = a,AC = b.\) Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Tính MN
-
A.
\(MN = \frac{{2ab}}{{a + b}}\)
-
B.
\(MN = \frac{{ab}}{{a + b}}\)
-
C.
\(MN = \frac{{ab}}{{2\left( {a + b} \right)}}\)
-
D.
\(MN = \frac{{ab}}{{a + b}}\)
Đáp án : B
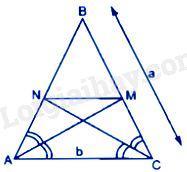
Xét tam giác ABC có AM là đường phân giác góc BAC nên \(\frac{{MB}}{{MC}} = \frac{{AB}}{{AC}} = \frac{a}{b}\)
Xét tam giác ABC có CN là đường phân giác góc BCA nên \(\frac{{NB}}{{NA}} = \frac{{CB}}{{AC}} = \frac{a}{b}\)
Do đó, \(\frac{{NB}}{{NA}} = \frac{{MB}}{{MC}}\) nên MN//AC (định lý Thalès đảo)
Ta có: \(\frac{{NB}}{{NA}} = \frac{{CB}}{{AC}} = \frac{a}{b} \Rightarrow \frac{{NB}}{{NB + NA}} = \frac{a}{{a + b}}\) hay \(\frac{{NB}}{{AB}} = \frac{a}{{a + b}}\)
Do đó, \(NB = \frac{{{a^2}}}{{a + b}}\)
Lại có: MN//AC nên \(\frac{{MN}}{{AC}} = \frac{{NB}}{{AB}}\) , do đó \(MN = \frac{{AC.NB}}{{AB}} = \frac{{ab}}{{a + b}}\)
Luyện tập và củng cố kiến thức Bài 2: Đường trung bình của tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Định lí Thalès trong tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 2: Xác suất lí thuyết và xác suất thực nghiệm Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Mô tả xác suất bằng tỉ số Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 3: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Các trường hợp đồng dạng của hai tam giác Toán 8 Chân trời sáng tạo