Trắc nghiệm Bài 2: Tứ giác Toán 8 Chân trời sáng tạo
Đề bài
Hãy chọn câu sai trong các câu sau
-
A.
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
-
B.
Tổng các góc của một tứ giác bằng 180 o.
-
C.
Tổng các góc của một tứ giác bằng 360o.
-
D.
Tứ giác ABCD là hình gồm các đoạn thẳng AB, BC, DC, DA , trong đó bất kì hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
Các góc của tứ giác có thể là
-
A.
4 góc nhọn.
-
B.
4 góc tù.
-
C.
4 góc vuông.
-
D.
1 góc vuông, 3 góc nhọn.
-
A.
Hai đỉnh kề nhau: A và B; A và D.
-
B.
Hai đỉnh đối nhau: A và C; B và D.
-
C.
Đường chéo: AC, BD.
-
D.
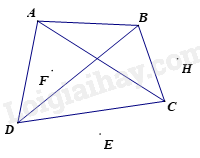
Các điểm nằm trong tứ giác là E, F và các điểm nằm ngoài tứ giác là H.
Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
-
A.
Tứ giác ABCD là hình gồm 4 đoạn thẳng: AB, BC, CD, DA.
-
B.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
-
C.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó hai đoạn thẳng kề một đỉnh song song với nhau.
-
D.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
-
A.
Hai cạnh đối nhau: AB, BC.
-
B.
Hai cạnh kề nhau: BC, DA.
-
C.
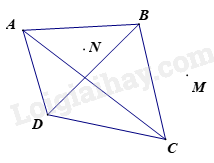
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
-
D.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
-
A.
\({220^o}\)
-
B.
\({200^o}\)
-
C.
\({160^o}\)
-
D.
\({130^o}\)
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
-
A.
\({113^o}\)
-
B.
\({107^o}\)
-
C.
\({58^o}\)
-
D.
\({83^o}\)
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
-
A.
\({160^o}\)
-
B.
\({167^o}\)
-
C.
\({170^o}\)
-
D.
\({130^o}\)
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
-
A.
\(\widehat C = {100^o};\widehat D = {80^o}\)
-
B.
\(\widehat C = {75^o};\widehat D = {55^o}\)
-
C.
\(\widehat C = {80^o};\widehat D = {60^o}\)
-
D.
\(\widehat C = {85^o};\widehat D = {65^o}\)
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
-
A.
10 cm
-
B.
50 cm
-
C.
20 cm
-
D.
30 cm
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
-
A.
\({100^o}\)
-
B.
\({130^o}\)
-
C.
\({80^o}\)
-
D.
\({210^o}\)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
-
A.
\(OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
-
B.
\(OA + OB + OC + O{{D}} > AB + BC + C{{D}} + DA\)
-
C.
\(OA + OB + OC + O{{D}} < \frac{1}{2}\left( {AB + BC + C{{D}} + DA} \right)\)
-
D.
\(OA - OB + OC - O{{D}} > AB + BC + C{{D}} + DA\)
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
-
A.
\({80^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
-
B.
\({90^o}{;^{}}{40^o}{;^{}}{70^o}{;^{}}{60^o}\)
-
C.
\({60^o}{;^{}}{80^o}{;^{}}{100^o}{;^{}}{120^o}\)
-
D.
\({60^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
-
A.
\({300^o}\)
-
B.
\({270^o}\)
-
C.
\({180^o}\)
-
D.
\({360^o}\)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
-
A.
\({160^o}\)
-
B.
\({260^o}\)
-
C.
\({180^o}\)
-
D.
\(100{}^o\)
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
-
A.
\(\widehat A = \widehat C = {95^o}\)
-
B.
\(\widehat A = {95^o};\widehat C = {55^o}\)
-
C.
\(\widehat A = \widehat C = {85^o}\)
-
D.
\(\widehat A = {55^o};\widehat C = {100^o}\)
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
-
A.
\(\widehat {BIC} = {100^o}{;^{}}\widehat {BKC} = {80^o}\)
-
B.
\(\widehat {BIC} = {90^o}{;^{}}\widehat {BKC} = {90^o}\)
-
C.
\(\widehat {BIC} = {60^o}{;^{}}\widehat {BKC} = {120^o}\)
-
D.
\(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
-
A.
1500
-
B.
1200
-
C.
1400
-
D.
1000
Lời giải và đáp án
Hãy chọn câu sai trong các câu sau
-
A.
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
-
B.
Tổng các góc của một tứ giác bằng 180 o.
-
C.
Tổng các góc của một tứ giác bằng 360o.
-
D.
Tứ giác ABCD là hình gồm các đoạn thẳng AB, BC, DC, DA , trong đó bất kì hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
Đáp án : B
Các góc của tứ giác có thể là
-
A.
4 góc nhọn.
-
B.
4 góc tù.
-
C.
4 góc vuông.
-
D.
1 góc vuông, 3 góc nhọn.
Đáp án : C
Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng 360o.
Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác.
-
A.
Hai đỉnh kề nhau: A và B; A và D.
-
B.
Hai đỉnh đối nhau: A và C; B và D.
-
C.
Đường chéo: AC, BD.
-
D.
Các điểm nằm trong tứ giác là E, F và các điểm nằm ngoài tứ giác là H.
Đáp án : D
Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
-
A.
Tứ giác ABCD là hình gồm 4 đoạn thẳng: AB, BC, CD, DA.
-
B.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
-
C.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó hai đoạn thẳng kề một đỉnh song song với nhau.
-
D.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
Đáp án : B
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
-
A.
Hai cạnh đối nhau: AB, BC.
-
B.
Hai cạnh kề nhau: BC, DA.
-
C.
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
-
D.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Đáp án : C
Từ hình vẽ ta thấy: Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
-
A.
\({220^o}\)
-
B.
\({200^o}\)
-
C.
\({160^o}\)
-
D.
\({130^o}\)
Đáp án : A
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C + \widehat D = {360^o} - \left( {\widehat A + \widehat B} \right) = {360^o} - {140^o} = {220^o}\end{array}\)
Tổng các góc trong một tứ giác bằng \({360^o}\)
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
-
A.
\({113^o}\)
-
B.
\({107^o}\)
-
C.
\({58^o}\)
-
D.
\({83^o}\)
Đáp án : C
Tính góc D trong tứ giác ABCD. Từ đó góc ngoài tại đỉnh D bằng \({180^o}\) trừ đi góc D trong tứ giác ABCD.
Góc ngoài và góc trong tứ giác tại một đỉnh là hai góc kề bù.
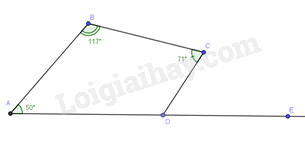
\(\widehat {C{{D}}E}\) là góc ngoài đỉnh D. Tứ giác ABCD có:
\(\begin{array}{l}\widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right)\\\widehat D = {360^o} - \left( {{{50}^o} + {{117}^o} + {{71}^o}} \right)\\\widehat D = {122^o}\end{array}\)
Vì \(\widehat {A{{D}}C}\) và \(\widehat {C{{D}}E}\) là hai góc kề bù nên:
\(\widehat {C{{D}}E} = {180^o} - \widehat D = {180^o} - {122^o} = {58^o}\)
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
-
A.
\({160^o}\)
-
B.
\({167^o}\)
-
C.
\({170^o}\)
-
D.
\({130^o}\)
Đáp án : B
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C = {360^o} - \widehat A - \widehat B - \widehat D = {360^o} - {50^o} - {123^o} - {20^o} = {167^o}\end{array}\)
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
-
A.
\(\widehat C = {100^o};\widehat D = {80^o}\)
-
B.
\(\widehat C = {75^o};\widehat D = {55^o}\)
-
C.
\(\widehat C = {80^o};\widehat D = {60^o}\)
-
D.
\(\widehat C = {85^o};\widehat D = {65^o}\)
Đáp án : C
Trong tứ giác ABCD ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra \(\widehat C + \widehat D = {360^o} - \widehat A - \widehat B = {360^o} - {100^o} - {120^o} = {140^o}(1)\)
Mà \(\widehat C - \widehat D = {20^o}\)(2)
Từ (1), (2) suy ra: \(\widehat C = \frac{140^o + 20^o}{2} = {80^o};\widehat D = \frac{140^o - 20^o}{2} = {60^o}\).
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
-
A.
10 cm
-
B.
50 cm
-
C.
20 cm
-
D.
30 cm
Đáp án : D
Gọi các cạnh AB, BC, CD, DA theo tỉ lệ 3, 5, 7, 9 nên ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9} = \frac{{AB + BC + C{{D}} + DA}}{{3 + 5 + 7 + 9}} = \frac{{240}}{{24}} = 10\)
Suy ra: AB = 3. 10 = 30 cm
BC = 5 .10 = 50 cm
CD = 7. 10 = 70 cm
DA = 9 .10 = 90 cm
Vậy cạnh ngắn nhất là canh AB có độ dài 30 cm
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
-
A.
\({100^o}\)
-
B.
\({130^o}\)
-
C.
\({80^o}\)
-
D.
\({210^o}\)
Đáp án : D
Tổng hai góc trong và góc ngoài tại một đỉnh của tứ giác bằng \({180^o}\)
Vì góc ngoài đỉnh D bằng \({50^o}\) nên góc trong tại đỉnh D là: \(\widehat D = {180^o} - {50^o} = {130^o}\)
Vì góc ngoài tại đỉnh A bằng \({100^o}\) nên góc trong tại đỉnh A là: \(\widehat A = {180^o} - {100^o} = {80^o}\)
Suy ra: \(\widehat A + \widehat D = {80^o} + {130^o} = {210^o}\)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
-
A.
\(OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
-
B.
\(OA + OB + OC + O{{D}} > AB + BC + C{{D}} + DA\)
-
C.
\(OA + OB + OC + O{{D}} < \frac{1}{2}\left( {AB + BC + C{{D}} + DA} \right)\)
-
D.
\(OA - OB + OC - O{{D}} > AB + BC + C{{D}} + DA\)
Đáp án : A
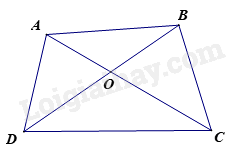
Xét tam giác ABC:
\(AB + BC > AC\) (bất đẳng thức tam giác)
Tương tự, lần lượt các tam giác BCD, CDA, DAB ta có:
\(\begin{array}{l}BC + C{{D}} > B{{D}}\\C{{D}} + DA > CA\\DA + AB > DB\end{array}\)
Cộng vế với vế ta được các bất đẳng thức trên ta được:
\(\begin{array}{l}AB + BC + C{{D}} + C{{D}} + DA + DA + AB > AC + B{{D}} + CA + DB\\ \Leftrightarrow 2\left( {AB + BC + C{{D}} + DA} \right) > 2\left( {AC + B{{D}}} \right)\\ \Leftrightarrow AB + BC + C{{D}} + DA > AC + B{{D}}\end{array}\)
Mà: \(AC + B{{D}} = OA + OC + OB + O{{D}}\) (hệ thức cộng đoạn thẳng)
\( \Leftrightarrow OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Vậy ta có: \(OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
-
A.
\({80^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
-
B.
\({90^o}{;^{}}{40^o}{;^{}}{70^o}{;^{}}{60^o}\)
-
C.
\({60^o}{;^{}}{80^o}{;^{}}{100^o}{;^{}}{120^o}\)
-
D.
\({60^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
Đáp án : A
\(\frac{{\widehat A}}{4} = \frac{{\widehat B}}{3} = \frac{{\widehat C}}{5} = \frac{{\widehat D}}{6} = \frac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}} = \frac{{{{360}^o}}}{{18}} = {20^o}\)
Do đó:
\(\begin{array}{l}\widehat A = {20^o}.4 = {80^o}\\\widehat B = {20^o}.3 = {60^o}\\\widehat C = {20^o}.5 = {100^o}\\\widehat D = {20^o}.6 = {120^o}\end{array}\)
Nên số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là \({80^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
Đáp án : B
Sử dụng định lí Pytago trong tam giác vuông.
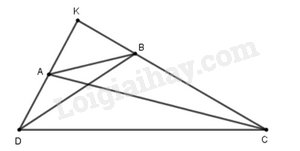
Gọi K là giao điểm AD, BC.
Vì \(\widehat C + \widehat D = {90^o}\) nên \(\widehat K = {90^o}\)
Áp dụng định lí Pytago trong tam giác vuông vào các tam giác:
+ ΔKAC vuông tại K ta có: AC2 = KC2 + KA2.
+ ΔKBD vuông tại K ta có: BD2 = KB2 + KD2.
+ ΔKBA vuông tại K ta có: BA2 = KA2 + KB2.
+ ΔKBD vuông tại K ta có: CD2 = KC2 + KD2.
Từ đó AC2+ BD2 = KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2) = AB2 + DC2.
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
-
A.
\({300^o}\)
-
B.
\({270^o}\)
-
C.
\({180^o}\)
-
D.
\({360^o}\)
Đáp án : D
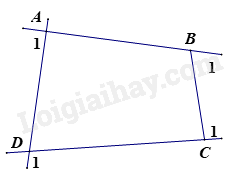
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
-
A.
\({160^o}\)
-
B.
\({260^o}\)
-
C.
\({180^o}\)
-
D.
\(100{}^o\)
Đáp án : A
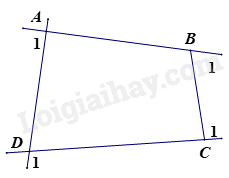
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \text{ suy ra } \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \text{ suy ra } \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \text{ suy ra } \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \text{ suy ra } \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Mà tổng số đo góc ngoài hai đỉnh B, c bằng \({200^o}\) nên tổng số đo góc ngoài tại hai đỉnh A, D bằng \({360^o} - {200^0} = {160^o}\)
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
-
A.
\(\widehat A = \widehat C = {95^o}\)
-
B.
\(\widehat A = {95^o};\widehat C = {55^o}\)
-
C.
\(\widehat A = \widehat C = {85^o}\)
-
D.
\(\widehat A = {55^o};\widehat C = {100^o}\)
Đáp án : A
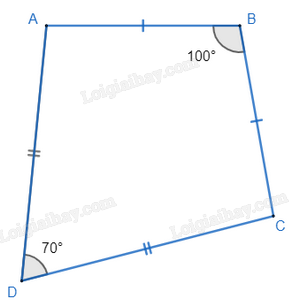
Xét tam giác ABC có AB = AC
\( \Rightarrow \Delta ABC\) cân tại B mà \(\widehat B = {100^o}\)
\( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{180}^o} - {{100}^o}}}{2} = {40^o}\)
Xét tam giác ADC có CD = DA
\( \Rightarrow \Delta A{{D}}C\) cân tại D có \(\widehat {A{{D}}C} = {70^o}\)
\( \Rightarrow \widehat {DAC} = \widehat {DCA} = \frac{{{{180}^o} - {{70}^o}}}{2} = {55^o}\)
Từ đó ta có:
\(\begin{array}{l}\widehat A = \widehat {BA{{D}}} = \widehat {BAC} + \widehat {CA{{D}}}\\ \Rightarrow \widehat A = \widehat {BA{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Và: \(\begin{array}{l}\widehat C = \widehat {BC{{D}}} = \widehat {BCA} + \widehat {AC{{D}}}\\ \Rightarrow \widehat C = \widehat {BC{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Vậy: \(\widehat A = \widehat C = {95^o}\)
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
-
A.
\(\widehat {BIC} = {100^o}{;^{}}\widehat {BKC} = {80^o}\)
-
B.
\(\widehat {BIC} = {90^o}{;^{}}\widehat {BKC} = {90^o}\)
-
C.
\(\widehat {BIC} = {60^o}{;^{}}\widehat {BKC} = {120^o}\)
-
D.
\(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Đáp án : D
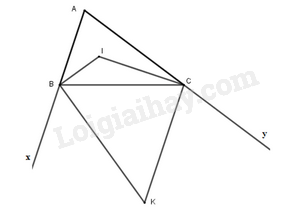
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat {ABC} + \widehat {BCA} = {180^o}\\ \Rightarrow \widehat {ABC} + \widehat {BCA} = {120^o}\end{array}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì CI là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \frac{1}{2}\widehat {BCA}\)
Từ đó:
\(\widehat {CBI} + \widehat {BCI} = \frac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \frac{1}{2}{.120^o} = {60^o}\)
Xét tam giác BCI có:
\(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = {180^o}\)
Nên: \(\widehat {BIC} = {180^o} - \left( {\widehat {BCI} + \widehat {CBI}} \right) = {180^o} - {60^o} = {120^o}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì BK là phân giác \(\widehat {CB{{x}}} \Rightarrow \widehat {CBK} = \frac{1}{2}\widehat {CBx}\)
Suy ra:
\(\widehat {CBK} + \widehat {CBI} = \frac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Hay \(\widehat {IBK} = {90^o}\)
Tương tự ta có: \(\widehat {ICK} = {90^o}\)
Xét tứ giác BICK có:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = {360^o}\\ \Rightarrow \widehat {BKC} = {360^o} - {90^o} - {90^o} - {120^o} = {60^o}\end{array}\)
Vậy \(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
-
A.
1500
-
B.
1200
-
C.
1400
-
D.
1000
Đáp án : A
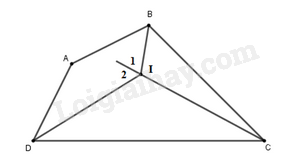
Xét tam giác BIC có:
\(\widehat {IBC} = \widehat {{I_1}} - \widehat {BCI}\)
Xét tam giác DIC có:
\(\widehat {I{{D}}C} = \widehat {{I_2}} - \widehat {IC{{D}}}\)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \left( {\widehat {{I_1}} + \widehat {{I_2}}} \right) - \left( {\widehat {{C_1}} + \widehat {{C_2}}} \right) = \widehat {BI{{D}}} - \widehat C\)
Tứ giác ABID:
\(\widehat {ABI} + \widehat {A{{D}}I} = {360^o} - \widehat A - \widehat {BI{{D}}}\)
Do: \(\widehat {ADI} = \widehat {I{{D}}C}\) (tính chất của tia phân giác)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \widehat {ABI} + \widehat {A{{D}}I}\)
Hay
\(\begin{array}{l}\widehat {BI{{D}}} - \widehat C = {360^o} - \widehat A - \widehat {BI{{D}}}\\ \Leftrightarrow 2\widehat {BI{{D}}} = {360^o} - \left( {\widehat A - \widehat C} \right) = {360^o} - {60^o} = {300^o}\end{array}\)
Suy ra: \(\widehat {BI{{D}}} = {150^o}\)
Luyện tập và củng cố kiến thức Bài 3: Hình thang - Hình thang cân Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Hình bình hành - Hình thoi Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Hình chữ nhật - Hình vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Định lí Pythagore Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 2: Xác suất lí thuyết và xác suất thực nghiệm Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Mô tả xác suất bằng tỉ số Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 3: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Các trường hợp đồng dạng của hai tam giác Toán 8 Chân trời sáng tạo