Trắc nghiệm Bài 3: Hình thang - Hình thang cân Toán 8 Chân trời sáng tạo
Đề bài
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
-
B.
Hình thang cân có hai cạnh bên bằng nhau.
-
C.
Hình thang cân có hai góc đối bù nhau.
-
D.
Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Hình thang cân là hình thang có
-
A.
hai góc kề bằng nhau.
-
B.
hai góc đối bằng nhau.
-
C.
hai cạnh đối bằng nhau.
-
D.
hai đường chéo bằng nhau.
Số trục đối xứng của hình thang cân là
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Tứ giác ABCD là hình thang vì có
-
A.
AB // CD.
-
B.
AB = CD .
-
C.
\(AB \bot C{{D}}\) .
-
D.
\(AB = C{{D}}\) .
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
-
A.
các đoạn thẳng AB và CD là các cạnh bên.
-
B.
các đoạn thẳng AB và CD là các cạnh đáy.
-
C.
các đoạn thẳng AB và CD là các đường chéo.
-
D.
các đoạn thẳng AB và CD là các đường cao.
Trong các tứ giác sau,tứ giác nào là hình thang?
-
A.
.
-
B.
.
-
C.
.
-
D.
.
-
A.
\({70^o}\)
-
B.
\({110^o}\)
-
C.
\({80^o}\)
-
D.
\({140^o}\)
Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
-
A.
12 cm
-
B.
13 cm
-
C.
7 cm
-
D.
6 cm
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
-
A.
Tam giác cân
-
B.
Tam giác nhọn
-
C.
Tam giác vuông
-
D.
Tam giác tù
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
-
A.
ABCD là hình thang cân
-
B.
AC = BD
-
C.
BC = AD
-
D.
Tam giác AOD cân tại C.
Cho hình thang ABCD (AB // CD) ta có:
-
A.
\(\widehat A + \widehat D = {180^o};\widehat C + \widehat B = {180^o}\)
-
B.
\(\widehat A + \widehat B = {180^o};\widehat C + \widehat D = {180^o}\)
-
C.
\(\widehat A + \widehat C = {180^o};\widehat B + \widehat D = {180^o}\)
-
D.
\(\widehat A + \widehat B + \widehat C + \widehat D = {180^o}\)
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
-
A.
\({130^o}\)
-
B.
\({100^o}\)
-
C.
\({80^o}\)
-
D.
\({50^o}\)
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
-
A.
\(\widehat D = {122^o}\)
-
B.
\(\widehat D = {212^o}\)
-
C.
\(\widehat D = {22^o}\)
-
D.
\(\widehat D = {0^o}\)
Tứ giác nào sau đây không phải hình thang:
-
A.
.
-
B.
.
-
C.
.
-
D.
.
Trong hình thang có hai góc tù:
-
A.
hai góc còn lại cũng là góc tù.
-
B.
hai góc còn lại là hai góc vuông.
-
C.
hai góc còn lại gồm một góc tù và một góc nhọn
-
D.
hai góc còn lại là hai góc nhọn.
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).
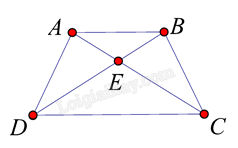
Tìm khẳng định đúng trong các khẳng định sau:
-
A.
\(\Delta ABC = \Delta BDA\)
-
B.
\(\widehat {CBA} = \widehat {DBA}\)
-
C.
\(\Delta ABE\) cân
-
D.
\(\Delta A{{ED}}\) cân
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
-
A.
Tam giác ABC vuông tại A.
-
B.
Tam giác ABC cân tại C.
-
C.
Tam giác ABC cân tại B.
-
D.
Tam giác ABC cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
-
A.
8cm
-
B.
11 cm
-
C.
12 cm
-
D.
13 cm
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
-
A.
6 cm
-
B.
8 cm
-
C.
9 cm
-
D.
12 cm
-
A.
\(\widehat A = \widehat C = {111^o}\)
-
B.
\(\widehat A = \widehat C = {130^o}\)
-
C.
\(\widehat A = {111^o};\widehat C = {130^o}\)
-
D.
\(\widehat A = {130^o};\widehat C = {111^o}\)
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
-
A.
\(\widehat {AM{{D}}} = {180^o}\)
-
B.
\(\widehat {AM{{D}}} = {150^o}\)
-
C.
\(\widehat {AM{{D}}} = {90^o}\)
-
D.
\(\widehat {AM{{D}}} = {60^o}\)
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
-
A.
\(\widehat A = {70^o};\widehat B = {135^o};\widehat C = {45^o};\widehat D = {110^o}\)
-
B.
\(\widehat A = {110^o};\widehat B = {135^o};\widehat C = {45^o};\widehat D = {70^o}\)
-
C.
\(\widehat A = {70^o};\widehat B = {45^o};\widehat C = {135^o};\widehat D = {110^o}\)
-
D.
\(\widehat A = {135^o};\widehat B = {70^o};\widehat C = {45^o};\widehat D = {110^o}\)
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
-
A.
\(\widehat {AC{{D}}} = {30^o}\)
-
B.
\(\widehat {AC{{D}}} = {45^o}\)
-
C.
\(\widehat {AC{{D}}} = {60^o}\)
-
D.
\(\widehat {AC{{D}}} = {90^o}\)
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
-
A.
\(B{{{D}}^2} - B{C^2} = C{{D}}{{.AB}}\)
-
B.
\(B{{{D}}^2} - B{C^2} = A{B^2}\)
-
C.
\(B{{{D}}^2} - B{C^2} = 2C{{D}}.AB\)
-
D.
\(B{{{D}}^2} - B{C^2} = BC.AB\)
Lời giải và đáp án
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
-
B.
Hình thang cân có hai cạnh bên bằng nhau.
-
C.
Hình thang cân có hai góc đối bù nhau.
-
D.
Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Đáp án : A
Dựa vào tính chất hình thang cân: Tứ giác có hai cạnh bên bằng nhau là hình thang cân là khẳng định sai, vì tứ giác có hai cạnh bên bằng nhau có thể là hình bình hành.
Hình thang cân là hình thang có
-
A.
hai góc kề bằng nhau.
-
B.
hai góc đối bằng nhau.
-
C.
hai cạnh đối bằng nhau.
-
D.
hai đường chéo bằng nhau.
Đáp án : D
Số trục đối xứng của hình thang cân là
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Đáp án : B
Tứ giác ABCD là hình thang vì có
-
A.
AB // CD.
-
B.
AB = CD .
-
C.
\(AB \bot C{{D}}\) .
-
D.
\(AB = C{{D}}\) .
Đáp án : A
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
-
A.
các đoạn thẳng AB và CD là các cạnh bên.
-
B.
các đoạn thẳng AB và CD là các cạnh đáy.
-
C.
các đoạn thẳng AB và CD là các đường chéo.
-
D.
các đoạn thẳng AB và CD là các đường cao.
Đáp án : B
Trong các tứ giác sau,tứ giác nào là hình thang?
-
A.
.
-
B.
.
-
C.
.
-
D.
.
Đáp án : C
Vậy tứ giác ABCD là hình thang
-
A.
\({70^o}\)
-
B.
\({110^o}\)
-
C.
\({80^o}\)
-
D.
\({140^o}\)
Đáp án : A
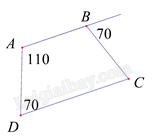
Tứ giác ABCD có \(\widehat A + \widehat D = {110^o} + {70^o} = {180^o}\) nên AB // CD suy ra ABCD là hình thang.
Mặt khác ta có: \(\widehat {ABC} = {180^o} - {70^o} = {110^o}\)
Hình thang ABCD có \(\widehat A = \widehat B = {110^o}\) . Suy ra ABCD là hình thang cân
Suy ra: \(\widehat C = \widehat D = {70^o}\)
Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
-
A.
12 cm
-
B.
13 cm
-
C.
7 cm
-
D.
6 cm
Đáp án : A
Hình thang cân có hai đường chéo bằng nhau.
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
-
A.
Tam giác cân
-
B.
Tam giác nhọn
-
C.
Tam giác vuông
-
D.
Tam giác tù
Đáp án : A
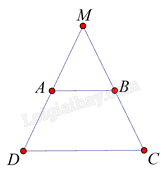
Vì ABCD là hình thang cân có hai đáy là AB và CD nên \(\widehat C = \widehat D\)
Mặt khác xét tam giác MCD có \(\widehat C = \widehat D\) . Suy ra tam giác MCD là tam giác cân.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
-
A.
ABCD là hình thang cân
-
B.
AC = BD
-
C.
BC = AD
-
D.
Tam giác AOD cân tại C.
Đáp án : D
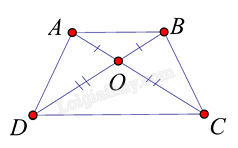
Ta có: \(OA = OB;OC = O{{D}} \Rightarrow OA + OC = OB + O{{D}} \Rightarrow AC = B{{D}}\)
Hình thang ABCD (AB //CD) có AC = BD nên ABCD là hình thang cân
Suy ra: BC = AD
Cho hình thang ABCD (AB // CD) ta có:
-
A.
\(\widehat A + \widehat D = {180^o};\widehat C + \widehat B = {180^o}\)
-
B.
\(\widehat A + \widehat B = {180^o};\widehat C + \widehat D = {180^o}\)
-
C.
\(\widehat A + \widehat C = {180^o};\widehat B + \widehat D = {180^o}\)
-
D.
\(\widehat A + \widehat B + \widehat C + \widehat D = {180^o}\)
Đáp án : A
Hình thang ABCD có AB // CD thì \(\widehat A\) và \(\widehat D\) ; \(\widehat B\) và \(\widehat C\) là các cặp góc trong cùng phía nên \(\widehat A + \widehat D = {180^o};\widehat B + \widehat D = {180^o}\)
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
-
A.
\({130^o}\)
-
B.
\({100^o}\)
-
C.
\({80^o}\)
-
D.
\({50^o}\)
Đáp án : C
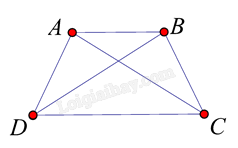
Giả sử ABCD là hình thang có đáy lớn là DC; đáy nhỏ là AB; \(\widehat C = \widehat D = {50^o}\) . Khi đó:
\(\widehat A = \widehat B = \frac{{{{360}^o} - \widehat C - \widehat D}}{2} = \frac{{{{360}^o} - {{50}^o} - {{50}^o}}}{2} = {130^o}\)
\( \Rightarrow \widehat B - \widehat C = \widehat A - \widehat D = {130^o} - {50^o} = {80^o}\)
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
-
A.
\(\widehat D = {122^o}\)
-
B.
\(\widehat D = {212^o}\)
-
C.
\(\widehat D = {22^o}\)
-
D.
\(\widehat D = {0^o}\)
Đáp án : A
Mà \(\widehat A = {58^o}\) nên \({58^o} + \widehat D = {180^o} \Rightarrow \widehat D = {180^o} - {58^o} = {122^o}\)
Tứ giác nào sau đây không phải hình thang:
-
A.
.
-
B.
.
-
C.
.
-
D.
.
Đáp án : D
Ta có: \(\widehat A + \widehat B = {126^o} + {55^o} = {181^o}\) nên Bc và AD không song song
Lại có: \(\widehat B \ne \widehat {BC{C_1}}\) nên AB và CD không song song với nhau
Vậy tứ giác ABCD ở hình D không phải là hình thang.
Trong hình thang có hai góc tù:
-
A.
hai góc còn lại cũng là góc tù.
-
B.
hai góc còn lại là hai góc vuông.
-
C.
hai góc còn lại gồm một góc tù và một góc nhọn
-
D.
hai góc còn lại là hai góc nhọn.
Đáp án : D
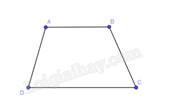
Xét hình thang ABCD có AB // CD nên \(\widehat A + \widehat D = {180^o}\) (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù.
Tương tự \(\widehat B\) và \(\widehat C\) cũng vậy.
Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn.
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).

Tìm khẳng định đúng trong các khẳng định sau:
-
A.
\(\Delta ABC = \Delta BDA\)
-
B.
\(\widehat {CBA} = \widehat {DBA}\)
-
C.
\(\Delta ABE\) cân
-
D.
\(\Delta A{{ED}}\) cân
Đáp án : C

Xét tam giác ABC và tam giác BAD có:
AB là cạnh chung
\(\widehat {ABC} = \widehat {BAC}\) (hai góc kề một đáy của hình thang cân)
BC = AD (hai cạnh bên của hình thang cân)
Suy ra: \(\Delta ABC = \Delta BA{{D}}\) (c – g – c). Suy ra: \(\widehat {CAB} = \widehat {DBA}\) (hai góc tương ứng)
Tam giác ABE có \(\widehat {E{{A}}B} = \widehat {EBA}\) nên suy ra tam giác ABE là tam giác cân.
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
-
A.
Tam giác ABC vuông tại A.
-
B.
Tam giác ABC cân tại C.
-
C.
Tam giác ABC cân tại B.
-
D.
Tam giác ABC cân tại A.
Đáp án : D
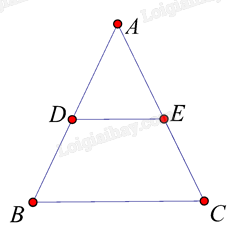
Tứ giác BDEC có DE // BC nên BDEC là hình thang . Để BDEC là hình thang cân thì \(\widehat B = \widehat C\) nên suy ra ABC là tam giác cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
-
A.
8cm
-
B.
11 cm
-
C.
12 cm
-
D.
13 cm
Đáp án : D
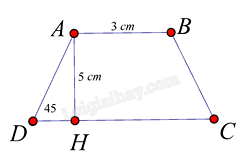
Ta có tam giác AHD vuông cân tại H vì \(\widehat D = {45^o}\) . Do đó DH = AH = 5 cm
Mà CD = AB + 2DH \( \Rightarrow C{{D}} = 3 + 2.5 = 13cm\)
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
-
A.
6 cm
-
B.
8 cm
-
C.
9 cm
-
D.
12 cm
Đáp án : D
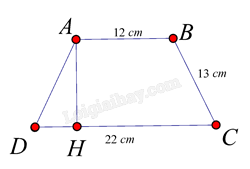
Xét hình thang cân ABCD có đáy lớn CD và đáy nhỏ AB đường cao AH ta có:
\(C{{D}} = AB + 2.DH \Rightarrow DH = \frac{{C{{D}} - AB}}{2} \Rightarrow DH = \frac{{22 - 12}}{2} = 5cm\)
Áp dụng định lí Pythago cho tam giác AHD vuông tại H có AD = BC = 13 cm và
DH = 5 cm ta có:
\(A{H^2} = A{{{D}}^2} - D{H^2} = {13^2} - {5^2} = 144 \Rightarrow AH = \sqrt {144} = 12cm\)
-
A.
\(\widehat A = \widehat C = {111^o}\)
-
B.
\(\widehat A = \widehat C = {130^o}\)
-
C.
\(\widehat A = {111^o};\widehat C = {130^o}\)
-
D.
\(\widehat A = {130^o};\widehat C = {111^o}\)
Đáp án : D
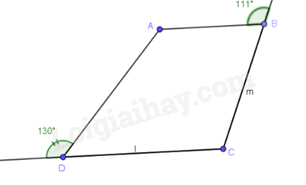
Hình thang ABCD có AB // CD nên \(\widehat A = \widehat {A{{D}}E} = {130^o};\widehat C = \widehat {ABF} = {111^o}\)
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
-
A.
\(\widehat {AM{{D}}} = {180^o}\)
-
B.
\(\widehat {AM{{D}}} = {150^o}\)
-
C.
\(\widehat {AM{{D}}} = {90^o}\)
-
D.
\(\widehat {AM{{D}}} = {60^o}\)
Đáp án : C
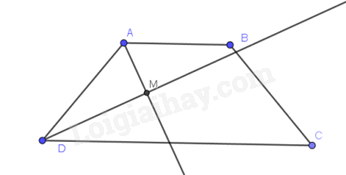
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M nên
\(\widehat {DAM} + \widehat {ADM} = \frac{1}{2}\left( {\widehat A + \widehat D} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Vậy \(\widehat {AM{{D}}} = {90^o}\)
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
-
A.
\(\widehat A = {70^o};\widehat B = {135^o};\widehat C = {45^o};\widehat D = {110^o}\)
-
B.
\(\widehat A = {110^o};\widehat B = {135^o};\widehat C = {45^o};\widehat D = {70^o}\)
-
C.
\(\widehat A = {70^o};\widehat B = {45^o};\widehat C = {135^o};\widehat D = {110^o}\)
-
D.
\(\widehat A = {135^o};\widehat B = {70^o};\widehat C = {45^o};\widehat D = {110^o}\)
Đáp án : B
Hình thang ABCD (AB // CD) có \(\widehat A + \widehat D = {180^o}\) mà \(\widehat A - \widehat D = {40^o}\)
\( \Rightarrow \widehat A = {220^o}:2 = {110^o}\)
Do đó: \(\widehat D = {180^o} - {110^o} = {70^o}\)
Lại có: \(\widehat B + \widehat C = {180^o}\) (2 góc trong cùng phía) mà \(\widehat B = 3\widehat C\) nên
\(4\widehat C = {180^o} \Rightarrow \widehat C = {180^o}:4 = {45^o}\)
Suy ra: \(\widehat B = 3\widehat C = {3.45^o} = {135^o}\)
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
-
A.
\(\widehat {AC{{D}}} = {30^o}\)
-
B.
\(\widehat {AC{{D}}} = {45^o}\)
-
C.
\(\widehat {AC{{D}}} = {60^o}\)
-
D.
\(\widehat {AC{{D}}} = {90^o}\)
Đáp án : D
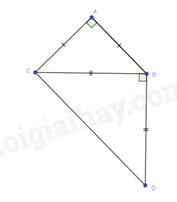
Xét tam giác BCD vuông cân tại B có \(\widehat {BC{{D}}} = \widehat {B{{D}}C} = {45^o}\) (2)
Từ (10, (2) suy ra: \(\widehat {ACB} + \widehat {BC{{D}}} = {90^o} = \widehat {AC{{D}}}\)
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
-
A.
\(B{{{D}}^2} - B{C^2} = C{{D}}{{.AB}}\)
-
B.
\(B{{{D}}^2} - B{C^2} = A{B^2}\)
-
C.
\(B{{{D}}^2} - B{C^2} = 2C{{D}}.AB\)
-
D.
\(B{{{D}}^2} - B{C^2} = BC.AB\)
Đáp án : A
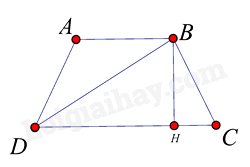
Kẻ \(BH \bot C{{D}}\) tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có: \(B{{{D}}^2} = D{H^2} + B{H^2}\)
Xét tam giác vuông CBH, theo định lý Pytago ta có: \(B{C^2} = C{H^2} + B{H^2}\)
Suy ra: \(B{{{D}}^2} - B{C^2} = D{H^2} - C{H^2} = \left( {DH + CH} \right)\left( {DH - CH} \right) = C{{D}}.AB\)
(Do DH + CH = CD; DH – CH = AB)
Luyện tập và củng cố kiến thức Bài 4: Hình bình hành - Hình thoi Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Hình chữ nhật - Hình vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tứ giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Định lí Pythagore Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 2: Xác suất lí thuyết và xác suất thực nghiệm Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Mô tả xác suất bằng tỉ số Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 3: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Các trường hợp đồng dạng của hai tam giác Toán 8 Chân trời sáng tạo