Trắc nghiệm Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều - hình chóp tứ giác đều Toán 8 Chân trời sáng tạo
Đề bài
Diện tích xung quanh của hình chóp tứ giác đều được tính bằng?
-
A.
tổng diện tích tất cả các mặt.
-
B.
tổng diện tích các mặt bên.
-
C.
diện tích mặt đáy.
-
D.
tổng diện tích một mặt bên và mặt đáy
Diện tích toàn phần của hình chóp tam giác đều được tính bằng?
-
A.
tổng diện tích các mặt bên.
-
B.
diện tích mặt đáy.
-
C.
tổng diện tích xung quanh và diện tích đáy.
-
D.
hiệu của diện tích xung quanh và diện tích đáy.
Cho hình chóp tam giác đều có diện tích một mặt bên là S. Công thức tính diện tích xung quanh của hình chóp tam giác đều bằng:
-
A.
\({S_{xq}} = \frac{S}{4}\).
-
B.
\({S_{xq}} = \frac{S}{3}\).
-
C.
\({S_{xq}} = 4.S\).
-
D.
. \({S_{xq}} = 3.S\).
Cho hình chóp tứ giác đều, thể tích của hình chóp được tính bằng:
-
A.
\(\frac{1}{3}\) tích của diện tích mặt đáy với chiều cao.
-
B.
\(\frac{1}{3}\) tích của diện tích mặt đáy với trung đoạn.
-
C.
tích của diện tích mặt đáy với chiều cao.
-
D.
tích của diện tích mặt đáy với trung đoạn.
Cho hình chóp tứ giác đều có diện tích xung quanh là \({S_{xq}}\). Diện tích một mặt của hình chóp tứ giác đều là:
-
A.
\(S = \frac{{{S_{xq}}}}{4}\).
-
B.
\(S = \frac{{{S_{xq}}}}{3}\).
-
C.
\(S = {S_{xq}}.3\).
-
D.
\(S = {S_{xq}}.4\).
Cho hình chóp tam giác đều có thể tích V, chiều cao h. Công thức tính diện tích mặt đáy S của hình chóp là:
-
A.
\(S = \frac{V}{h}\)
-
B.
\(S = \frac{{3V}}{h}\)
-
C.
\(S = \frac{V}{{3h}}\)
-
D.
\(S = 3V.h\)
Tính diện tích xung quanh của hình chóp tứ giác đều biết chiều cao một mặt bên của hình chóp bằng 5cm, cạnh đáy của hình chóp bằng 4cm.
-
A.
\(20c{m^2}\).
-
B.
\(60c{m^2}\).
-
C.
\(40c{m^2}\)
-
D.
\(80c{m^2}\)
Cho hình chóp tam giác đều có diện tích một mặt bên là \(50c{m^2}\).Tính diện tích xung quanh của hình chóp đó.
-
A.
\(50c{m^2}\).
-
B.
\(\frac{{100}}{3}c{m^2}\)
-
C.
\(150c{m^2}\).
-
D.
\(100c{m^2}\).
Chọn câu trả lời sai trong các câu sau:
-
A.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên.
-
B.
Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy.
-
C.
Thể tích của hình chóp tam giác đều bằng tích của diện tích đáy với chiều cao.
-
D.
Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao.
Cho hình chóp tam giác đều có thể tích là \(250c{m^3}\), chiều cao hình chóp bằng \(30cm\). Tính diện tích mặt đáy của hình chóp đó.
-
A.
\(7500c{m^2}\).
-
B.
\(25c{m^2}\)
-
C.
\(250c{m^2}\).
-
D.
\(\frac{{25}}{3}c{m^2}\).
Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là \(9cm\). Tính thể tích của hình chóp đó.
-
A.
\(48c{m^3}\).
-
B.
\(144c{m^3}\)
-
C.
\(72c{m^3}\).
-
D.
\(36c{m^3}\).
Cho hình chóp tam giác đều S.ABC có các mặt bên là các tam giác cân diện tích \(10c{m^2}\), diện tích mặt đáy là \(20c{m^2}\). Tính diện tích toàn phần của hình chóp đó.
-
A.
\(50c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Tính diện tích bìa cần để làm một hộp quà hình chóp tam giác đều có bốn mặt là tam giác đều bằng nhau cạnh 4,4cm và chiều cao mặt đáy bằng 3cm ( không tính mép dán)
-
A.
\(24,6c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(26,4c{m^2}\).
. Một chiếc bánh hình chóp tam giác đều có chiều cao của hình chóp là \(9cm\), tam giác đáy có cạnh đáy bằng 4cm , chiều cao bằng \(2\sqrt 2 cm\).Tính thể tích của chiếc bánh đó.
-
A.
\(12c{m^3}\).
-
B.
\(24c{m^3}\)
-
C.
\(12\sqrt 2 c{m^3}\).
-
D.
\(24\sqrt 2 c{m^3}\).
Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ:
-
A.
Giảm đi 9 lần.
-
B.
Tăng lên 3 lần.
-
C.
Giảm đi 3 lần.
-
D.
Tăng lên 9 lần.
Cho hình chóp tam giác đều có thể tích là \(250c{m^2}\), diện tích đáy bằng\(50c{m^2}\). Tính chiều cao của hình chóp đó.
-
A.
\(15cm\).
-
B.
\(5cm\)
-
C.
\(10cm\).
-
D.
\(25cm\).
Một hình chóp tứ giác đều có thể tích bằng \(50c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 4cm. Tính diện tích xung quanh hình chóp đó.
-
A.
\(40(c{m^2})\)
-
B.
\(50(c{m^2})\)
-
C.
\(60(c{m^2})\)
-
D.
\(80(c{m^2})\)
Cho hình chóp tam giác đều nằm trong một lăng trụ đứng đáy là tam giác đều như hình, Biết diện tích xung quanh của lăng trụ đứng bằng \(36c{m^2}\), chiều cao mặt đáy bằng \(2\sqrt 3 cm\), cạnh đáy bằng 4cm. Tính thể tích hình chóp tam giác đều.
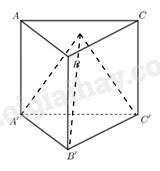
-
A.
\(4c{m^3}\).
-
B.
\(4\sqrt 3 c{m^3}\).
-
C.
\(8\sqrt 3 c{m^3}\).
-
D.
\(8c{m^3}\).
Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng \(72c{m^2}\) , chiều cao có độ dài bằng 6cm, chiều cao một mặt bên là 4cm .Thể tích của khối chóp đó là?
-
A.
\(36c{m^3}\).
-
B.
\(162c{m^3}\).
-
C.
\(162\sqrt 3 c{m^3}\).
-
D.
\(72c{m^3}\).
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{81\sqrt 3 }}{4}c{m^3}\).
-
B.
\(\frac{{27\sqrt 3 }}{8}c{m^3}\).
-
C.
\(\frac{{81\sqrt 3 }}{8}c{m^3}\).
-
D.
\(\frac{{27\sqrt 3 }}{4}c{m^3}\).
Một người định làm một chiếc đèn trang trí dạng hình chóp tam giác đều. Chu vi mặt đáy bằng 90cm, chiều cao một mặt bên bằng 60cm. Người ta sẽ dán các mặt xung quanh đèn bằng giấy màu. Tính số tiền người người đó mua giấy màu để dán đèn, biết \(1{m^2}\) có giá 120000 đồng.

-
A.
32400 đồng.
-
B.
324000 đồng.
-
C.
3240 đồng.
-
D.
3240000 đồng.
Một cái bể hình hộp chữ nhật đựng nước, có chiều dài 1,2m; chiều rộng 0,9m, chiều cao 1m. Hiện tại mực nước trong bể cao 0,5m. Người ta dùng 1 chiếc gầu hình chóp tam giác đều diện tích đáy \(1800c{m^2}\), chiều cao 20cm để múc nước vào bể. Cần múc bao nhiêu lần để đầy nước trong bể? (mỗi lần múc đầy gầu)
-
A.
25 lần.
-
B.
15 lần.
-
C.
45 lần.
-
D.
30 lần.
Một khối gỗ gồm hai phần: phần đế là hình lập phương cạnh 60cm và phần hình chóp tứ giác đều có chiều cao 40cm. Tính thể tích khối gỗ theo đơn vị mét khối.
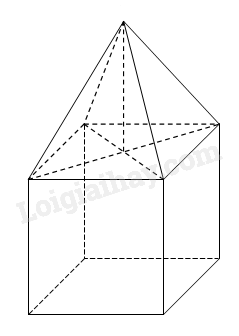
-
A.
\(0,248{m^3}\).
-
B.
\(268{m^3}\).
-
C.
\(264{m^3}\).
-
D.
\(0,264{m^3}\).
Một bể cá cảnh hình hộp chữ nhật có hai cạnh đáy là 25cm và 40cm. Mực nước trong bể ban đầu cách miệng bể là 20cm. Người ta đang bỏ bên trong một vật trang trí hình chóp tứ giác đều cạnh đáy 20cm và chiều cao 12cm. Hỏi khi lấy khối đá ra thì mực nước khi đó cách miệng bể bao nhiêu?
-
A.
\(21,6cm\).
-
B.
\(18,4cm\).
- C.
-
D.
\(20cm\).
Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)
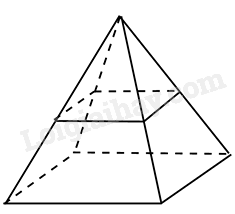
-
A.
16 người.
-
B.
20 người.
-
C.
18 người.
-
D.
14 người.
Lời giải và đáp án
Diện tích xung quanh của hình chóp tứ giác đều được tính bằng?
-
A.
tổng diện tích tất cả các mặt.
-
B.
tổng diện tích các mặt bên.
-
C.
diện tích mặt đáy.
-
D.
tổng diện tích một mặt bên và mặt đáy
Đáp án : B
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên nên chọn đáp án B
Diện tích toàn phần của hình chóp tam giác đều được tính bằng?
-
A.
tổng diện tích các mặt bên.
-
B.
diện tích mặt đáy.
-
C.
tổng diện tích xung quanh và diện tích đáy.
-
D.
hiệu của diện tích xung quanh và diện tích đáy.
Đáp án : C
Sử dụng công thức tính diện tích toàn phần của hình chóp tam giác đều.
Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy nên chọn đáp án C.
Cho hình chóp tam giác đều có diện tích một mặt bên là S. Công thức tính diện tích xung quanh của hình chóp tam giác đều bằng:
-
A.
\({S_{xq}} = \frac{S}{4}\).
-
B.
\({S_{xq}} = \frac{S}{3}\).
-
C.
\({S_{xq}} = 4.S\).
-
D.
. \({S_{xq}} = 3.S\).
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều.
Diện tích xung quanh của hình chóp tam giác đều bằng tổng diện tích các mặt bên mà hình chóp tam giác đều có ba mặt bên nên diện tích xung quanh của hình chóp tam giác đều bằng S+S+S =3.S nên chọn đáp án D
Cho hình chóp tứ giác đều, thể tích của hình chóp được tính bằng:
-
A.
\(\frac{1}{3}\) tích của diện tích mặt đáy với chiều cao.
-
B.
\(\frac{1}{3}\) tích của diện tích mặt đáy với trung đoạn.
-
C.
tích của diện tích mặt đáy với chiều cao.
-
D.
tích của diện tích mặt đáy với trung đoạn.
Đáp án : A
Sử dụng công thức tính thể tích của hình chóp tứ giác đều.
Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó nên chọn đáp án A
Cho hình chóp tứ giác đều có diện tích xung quanh là \({S_{xq}}\). Diện tích một mặt của hình chóp tứ giác đều là:
-
A.
\(S = \frac{{{S_{xq}}}}{4}\).
-
B.
\(S = \frac{{{S_{xq}}}}{3}\).
-
C.
\(S = {S_{xq}}.3\).
-
D.
\(S = {S_{xq}}.4\).
Đáp án : A
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên mà hình chóp tứ giác đều có 4 mặt bên nên \({S_{xq}} = S.4 \Rightarrow S = \frac{{{S_{xq}}}}{4}\) nên chọn đáp án A
Cho hình chóp tam giác đều có thể tích V, chiều cao h. Công thức tính diện tích mặt đáy S của hình chóp là:
-
A.
\(S = \frac{V}{h}\)
-
B.
\(S = \frac{{3V}}{h}\)
-
C.
\(S = \frac{V}{{3h}}\)
-
D.
\(S = 3V.h\)
Đáp án : B
Sử dụng công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\)
\( = > S = \frac{{3V}}{h}\)
Tính diện tích xung quanh của hình chóp tứ giác đều biết chiều cao một mặt bên của hình chóp bằng 5cm, cạnh đáy của hình chóp bằng 4cm.
-
A.
\(20c{m^2}\).
-
B.
\(60c{m^2}\).
-
C.
\(40c{m^2}\)
-
D.
\(80c{m^2}\)
Đáp án : C
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên mà hình chóp tứ giác đều có 4 mặt bên nên \({S_{xq}} = S.4 = (\frac{1}{2}.5.4).4 = 40c{m^2}\) nên chọn đáp án C.
Cho hình chóp tam giác đều có diện tích một mặt bên là \(50c{m^2}\).Tính diện tích xung quanh của hình chóp đó.
-
A.
\(50c{m^2}\).
-
B.
\(\frac{{100}}{3}c{m^2}\)
-
C.
\(150c{m^2}\).
-
D.
\(100c{m^2}\).
Đáp án : C
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều: \({S_{xq}} = {S_{1mat}}.3\)
Theo công thức tính diện tích xung quanh của hình chóp tam giác đều:
\({S_{xq}} = 50.3 = 150c{m^2}\)
Chọn câu trả lời sai trong các câu sau:
-
A.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên.
-
B.
Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy.
-
C.
Thể tích của hình chóp tam giác đều bằng tích của diện tích đáy với chiều cao.
-
D.
Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao.
Đáp án : C
Sử dụng công thức tính diện tích xung quanh, diện tích toàn phần của hình chóp tứ giác đều, hình chóp tam giác đều.
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên nên A đúng
Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy nên B đúng
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\)tích của diện tích đáy với chiều cao nên C sai
Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao nên D đúng
Cho hình chóp tam giác đều có thể tích là \(250c{m^3}\), chiều cao hình chóp bằng \(30cm\). Tính diện tích mặt đáy của hình chóp đó.
-
A.
\(7500c{m^2}\).
-
B.
\(25c{m^2}\)
-
C.
\(250c{m^2}\).
-
D.
\(\frac{{25}}{3}c{m^2}\).
Đáp án : B
Sử dụng công thức tính thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức tính thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
\( = > S = \frac{{3V}}{h} = \frac{{3.250}}{{30}} = 25c{m^2}\)
Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là \(9cm\). Tính thể tích của hình chóp đó.
-
A.
\(48c{m^3}\).
-
B.
\(144c{m^3}\)
-
C.
\(72c{m^3}\).
-
D.
\(36c{m^3}\).
Đáp án : A
Sử dụng công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h = \frac{1}{3}.(4.4).9 = 48c{m^3}\)
Cho hình chóp tam giác đều S.ABC có các mặt bên là các tam giác cân diện tích \(10c{m^2}\), diện tích mặt đáy là \(20c{m^2}\). Tính diện tích toàn phần của hình chóp đó.
-
A.
\(50c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Đáp án : A
Dựa vào công thức tính diện tích toàn phần của hình chóp tam giác đều: \({S_{tp}} = {S_{xq}} + {S_{day}}\)
Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy. Vậy diện tích toàn phần của hình chóp S.ABC là \({S_{tp}} = {S_{xq}} + {S_{day}} = 3.10 + 20 = 50c{m^2}\)
Tính diện tích bìa cần để làm một hộp quà hình chóp tam giác đều có bốn mặt là tam giác đều bằng nhau cạnh 4,4cm và chiều cao mặt đáy bằng 3cm ( không tính mép dán)
-
A.
\(24,6c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(26,4c{m^2}\).
Đáp án : D
Dựa vào công thức tính diện tích toàn phần của hình chóp tam giác đều:\({S_{tp}} = {S_{xq}} + {S_{day}}\)
Vì tất cả các mặt đều là tam giác đều bằng nhau nên diện tích của các mặt đều bằng nhau.
Do đó diện tích bìa chính là tổng diện tích 4 mặt của hình chóp tam giác đều.
Khi đó diện tích bìa cần dùng là:
\({S_{tp}} = {S_{xq}} + {S_{đáy}} = 4.{S_{một \; mặt}} = 4.(\frac{1}{2}.4,4.3) = 26,4c{m^2}\)
. Một chiếc bánh hình chóp tam giác đều có chiều cao của hình chóp là \(9cm\), tam giác đáy có cạnh đáy bằng 4cm , chiều cao bằng \(2\sqrt 2 cm\).Tính thể tích của chiếc bánh đó.
-
A.
\(12c{m^3}\).
-
B.
\(24c{m^3}\)
-
C.
\(12\sqrt 2 c{m^3}\).
-
D.
\(24\sqrt 2 c{m^3}\).
Đáp án : C
Sử dụng công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức thể tích của hình chóp tam giác đều, thể tích chiếc bánh là: \(V = \frac{1}{3}.S.h = \frac{1}{3}.(\frac{1}{2}.4.2\sqrt 2 ).9 = 12\sqrt 2 c{m^3}\)
Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ:
-
A.
Giảm đi 9 lần.
-
B.
Tăng lên 3 lần.
-
C.
Giảm đi 3 lần.
-
D.
Tăng lên 9 lần.
Đáp án : B
Dựa vào công thức tính thể tích khối chóp
Nếu cạnh đáy tăng lên 3 lần thì diện tích đáy tăng 9 lần. Vì chiều cao giảm đi 3 lần nên thể tích khối chóp tăng lên 3 lần.
Cho hình chóp tam giác đều có thể tích là \(250c{m^2}\), diện tích đáy bằng\(50c{m^2}\). Tính chiều cao của hình chóp đó.
-
A.
\(15cm\).
-
B.
\(5cm\)
-
C.
\(10cm\).
-
D.
\(25cm\).
Đáp án : A
Sử dụng công thức tính thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức tính thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\)
\( = > h = \frac{{3V}}{S} = \frac{{3.250}}{{50}} = 15cm\).
Một hình chóp tứ giác đều có thể tích bằng \(50c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 4cm. Tính diện tích xung quanh hình chóp đó.
-
A.
\(40(c{m^2})\)
-
B.
\(50(c{m^2})\)
-
C.
\(60(c{m^2})\)
-
D.
\(80(c{m^2})\)
Đáp án : A
B1: Tính diện tích đáy.
B2: Gọi x là độ dài cạnh đáy , tính diện tích đáy theo x, từ đó tìm được x.
B3: Tính diện tích một mặt bên.
B4: Tính diện tích xung quanh của hình chóp.
Diện tích đáy của hình chóp là : \(50.3:6 = 25c{m^2}\)
Gọi x là độ dài cạnh đáy, vì đáy hình chóp tứ giác đều là hình vuông nên ta có
\({x^2} = 25 \Rightarrow x = 5cm\).
Diện tích một mặt bên là: \(S = \frac{1}{2}.5.4 = 10(c{m^2})\)
Diện tích xung quanh của hình chóp trên là: \({S_{xq}} = 4.S = 4.10 = 40(c{m^2})\)
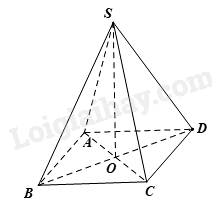
Cho hình chóp tam giác đều nằm trong một lăng trụ đứng đáy là tam giác đều như hình, Biết diện tích xung quanh của lăng trụ đứng bằng \(36c{m^2}\), chiều cao mặt đáy bằng \(2\sqrt 3 cm\), cạnh đáy bằng 4cm. Tính thể tích hình chóp tam giác đều.

-
A.
\(4c{m^3}\).
-
B.
\(4\sqrt 3 c{m^3}\).
-
C.
\(8\sqrt 3 c{m^3}\).
-
D.
\(8c{m^3}\).
Đáp án : B
B1: Tính chu vi đáy dựa vào công thức tính diện tích xung quanh hình lăng trụ đứng đáy là tam giác đều: \({S_{xq}} = C.h\)
B2: Tính chiều cao hình lăng trụ đứng, từ đó suy ra chiều cao hình chóp tam giác đều.
B3: Tính thể tích hình chóp đều theo công thức.
Chu vi đáy ABC là: \(C = 4 + 4 + 4 = 12(cm)\)
Chiều cao hình lăng trụ đứng là: \(h = {S_{xq}}:C = 36:12 = 3(cm)\)
Từ hình vẽ ta thấy chiều cao hình chóp tam giác đều bằng chiều cao hình lăng trụ đứng đáy là tam giác đều nên chiều cao hình chóp bằng 3cm.
Diện tích mặt đáy bằng: \({S_{ABC}} = \frac{1}{2}.4.2\sqrt 3 = 4\sqrt 3 (c{m^2})\)
Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.{S_{ABC}}.h = \frac{1}{3}.4\sqrt 3 .3 = 4\sqrt 3 c{m^3}\)
Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng \(72c{m^2}\) , chiều cao có độ dài bằng 6cm, chiều cao một mặt bên là 4cm .Thể tích của khối chóp đó là?
-
A.
\(36c{m^3}\).
-
B.
\(162c{m^3}\).
-
C.
\(162\sqrt 3 c{m^3}\).
-
D.
\(72c{m^3}\).
Đáp án : B
B1: Tính độ dài cạnh đáy.
B2: Tính diện tích mặt đáy.
B3: Tính thể tích hình chóp đều theo công thức.
Diện tích một mặt bên là: \(72:4 = 18c{m^2}\)
Độ dài cạnh đáy là: \(18.2:4 = 9cm\)
Diện tích mặt đáy là: \({S_{ABCD}} = 9.9 = 81c{m^2}\)
Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.81.6 = 162c{m^3}\)
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{81\sqrt 3 }}{4}c{m^3}\).
-
B.
\(\frac{{27\sqrt 3 }}{8}c{m^3}\).
-
C.
\(\frac{{81\sqrt 3 }}{8}c{m^3}\).
-
D.
\(\frac{{27\sqrt 3 }}{4}c{m^3}\).
Đáp án : B
Sử dụng kiến thức về hình chóp đều, chu vi tam giác để tính.
B1: Tính độ dài cạnh đáy dựa vào chu vi.
B2: Tính chiều cao hình chóp dựa vào điều kiện đề bài.
B3: Tính diện tích mặt đáy.
B4: Tính thể tích hình chóp theo công thức.
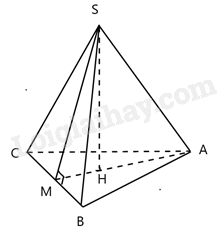
Tam giác ABC đều nên \(AB = BC = CA\)
Vì chu vi tam giác ABC bằng 9cm nên
\(AB + BC + CA = 9\)
\(\begin{array}{l} \Rightarrow 3.BC = 9\\ \Rightarrow BC = 3(cm)\end{array}\)
Gọi H là trọng tâm tam giác ABC, M là trung điểm BC.
Khi đó SH là chiều cao của hình chóp \( \Rightarrow SH = \frac{3}{2}.BC = \frac{3}{2}.3 = \frac{9}{2}(cm)\)
AM là trung tuyến của tam giác đều ABC nên AM đồng thời là đường cao của đáy\( \Rightarrow AM = \frac{{3\sqrt 3 }}{2}(cm)\)
\({S_{ABC}} = \frac{1}{2}.BC.AM = \frac{1}{2}.3.\frac{{3\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{4}(c{m^2})\)
\({V_{ABC}} = \frac{1}{3}.{S_{ABC}}.SH = \frac{1}{3}.\frac{{9\sqrt 3 }}{4}.\frac{9}{2} = \frac{{27\sqrt 3 }}{8}(c{m^3})\)
Một người định làm một chiếc đèn trang trí dạng hình chóp tam giác đều. Chu vi mặt đáy bằng 90cm, chiều cao một mặt bên bằng 60cm. Người ta sẽ dán các mặt xung quanh đèn bằng giấy màu. Tính số tiền người người đó mua giấy màu để dán đèn, biết \(1{m^2}\) có giá 120000 đồng.

-
A.
32400 đồng.
-
B.
324000 đồng.
-
C.
3240 đồng.
-
D.
3240000 đồng.
Đáp án : D
B1: Tính cạnh của mặt đáy.
B2: Tính diện tích một mặt hình chóp.
B3: Áp dụng công thức tính diện tích xung quanh của hình chóp \({S_{xq}} = S.3\).
B4: Tính số tiền mua giấy.
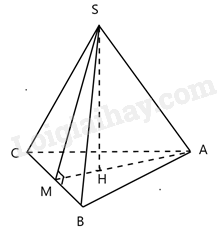
Cạnh của mặt đáy là: \(90:3 = 30(cm)\)
Diện tích một mặt bên bằng: \({S_{SBC}} = \frac{1}{2}.60.30 = 900c{m^2}\)
Diện tích giấy người đó cần dùng là: \({S_{xq}} = {S_{SAB}}.3 = 900.3 = 2700c{m^2} = 0,27{m^2}\)
Số tiền người người đó mua giấy màu để dán đèn: \(0,27.120000 = 32400\)(đồng).
Một cái bể hình hộp chữ nhật đựng nước, có chiều dài 1,2m; chiều rộng 0,9m, chiều cao 1m. Hiện tại mực nước trong bể cao 0,5m. Người ta dùng 1 chiếc gầu hình chóp tam giác đều diện tích đáy \(1800c{m^2}\), chiều cao 20cm để múc nước vào bể. Cần múc bao nhiêu lần để đầy nước trong bể? (mỗi lần múc đầy gầu)
-
A.
25 lần.
-
B.
15 lần.
-
C.
45 lần.
-
D.
30 lần.
Đáp án : C
B1: Tính thể tích nước trong bể bằng công thức tính thể tích hình hộp chữ nhật.
B2: Tính thể tích gầu hình chóp tam giác đều.
B3: Tính số lần múc nước.
Thể tích nước cần để đổ vào bể là:
\({V_{nuoc}} = 1,2.0,9.(1 - 0,5) = 0,54({m^3}) = 540\)(lít)
Thể tích gầu nước là:
\({V_{gau}} = \frac{1}{3}.1800.20 = 12000(c{m^3}) = 12\)(lít)
Số lần cần múc để hết nước trong bể là: \(540:12 = 45\)(lần)
Một khối gỗ gồm hai phần: phần đế là hình lập phương cạnh 60cm và phần hình chóp tứ giác đều có chiều cao 40cm. Tính thể tích khối gỗ theo đơn vị mét khối.

-
A.
\(0,248{m^3}\).
-
B.
\(268{m^3}\).
-
C.
\(264{m^3}\).
-
D.
\(0,264{m^3}\).
Đáp án : D
B1: Tính thể tích phần đế hình lập phương.
B2: Tính thể tích phần hình chóp tứ giác đều.
B3: Tính thể tích khối gỗ.
Tính thể tích phần đế hình lập phương: \({V_1} = 60.60.60 = 216000c{m^3}\)
Tính thể tích phần hình chóp tứ giác đều: \({V_2} = \frac{1}{3}.(60.60).40 = 48000c{m^3}\)
Tính thể tích khối gỗ: \(V = {V_1} + {V_2} = 216000 + 48000 = 264000c{m^3} = 0,264{m^3}\)
Một bể cá cảnh hình hộp chữ nhật có hai cạnh đáy là 25cm và 40cm. Mực nước trong bể ban đầu cách miệng bể là 20cm. Người ta đang bỏ bên trong một vật trang trí hình chóp tứ giác đều cạnh đáy 20cm và chiều cao 12cm. Hỏi khi lấy khối đá ra thì mực nước khi đó cách miệng bể bao nhiêu?
-
A.
\(21,6cm\).
-
B.
\(18,4cm\).
- C.
-
D.
\(20cm\).
Đáp án : A
Sử dụng kiến thức về hình chóp tứ giác đều, hình hộp chữ nhật để tính.
Thể tích của vật trang trí đó là: \(\frac{1}{3}.(20.20).12 = 1600c{m^3}\)
Thể tích phần nước hụt đi chính bằng thể tích của vật trang trí đó nên thể tích phần nước hụt đi là \({V_1} = 1600c{m^3}\)
Diện tích đáy bể cá là: \(25.40 = 1000c{m^2}\)
Chiều cao phần mực nước hụt đi là: \({h_1} = \frac{{{V_1}}}{{{S_{day}}}} = \frac{{1600}}{{1000}} = 1,6cm\)
Khi lấy khối đá ra mực nước giảm đi 1,6cm nên mực nước ban đầu cách miệng bể là \(20 + 1,6 = 21,6cm\).
Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)

-
A.
16 người.
-
B.
20 người.
-
C.
18 người.
-
D.
14 người.
Đáp án : D
Sử dụng kiến thức về hình chóp tứ giác đều, thể tích hình chóp đều để tính.
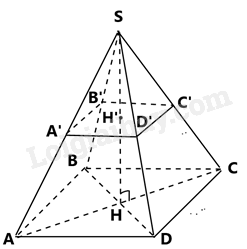
\(SH = 4m\)là chiều cao của bugalow
\( \Rightarrow SH' = \frac{{SH}}{2} = 2m\)
\(A'B' = \frac{1}{2}.AB = \frac{1}{2}.6 = 3m\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'D'}} = 3.3 = 9{m^2}\\{S_{ABCD}} = 6.6 = 36{m^2}\end{array}\)
\(\begin{array}{l}{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}.SH' = \frac{1}{3}.9.2 = 6{m^3}\\{V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.36.4 = 48{m^3}\end{array}\)
Thể tích phần không gian còn lại ở tầng dưới là: \(V = {V_{S.ABCD}} - {V_{S.A'B'C'D'}} = 48 - 6 = 42{m^3}\)
- Trắc nghiệm Bài 2: Xác suất lí thuyết và xác suất thực nghiệm Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Mô tả xác suất bằng tỉ số Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 3: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Các trường hợp đồng dạng của hai tam giác Toán 8 Chân trời sáng tạo









