Cho hình vẽ:
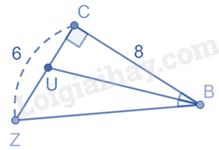
Độ dài đoạn thẳng UC là:
-
A.
\(\frac{8}{3}\)
-
B.
3
-
C.
\(\frac{{10}}{3}\)
-
D.
Đáp án khác
Tam giác BCZ vuông tại C nên theo định lý Pytago ta có:
\(BZ = \sqrt {B{C^2} + C{Z^2}} = 10\)
Trong tam giác BCZ có BU là đường phân giác của góc CBZ nên \(\frac{{UC}}{{UZ}} = \frac{{BC}}{{BZ}} = \frac{8}{{10}} = \frac{4}{5}\)
Do đó, \(\frac{{UC}}{4} = \frac{{UZ}}{5}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{UC}}{4} = \frac{{UZ}}{5} = \frac{{UC + UZ}}{{4 + 5}} = \frac{{CZ}}{9} = \frac{6}{9} = \frac{2}{3}\) nên \(UC = 4.\frac{2}{3} = \frac{8}{3}\)
Đáp án : A
Các bài tập cùng chuyên đề
Trong tam giác, đường… chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Từ (cụm từ) thích hợp điền vào dấu … để được đáp án đúng là
Cho tam giác ABC có AD là phân giác trong của góc A. Khi đó,
Cho hình vẽ:
Chọn đáp án đúng
Cho tam giác ABC có AD là đường phân giác của tam giác. Biết rằng \(BD = 3cm,DC = 4cm.\) Khi đó, tỉ số \(\frac{{AB}}{{AC}}\) bằng:
Đáp án nào dưới đây có tỉ số \(\frac{{BD}}{{DC}} = \frac{3}{4}\) ?
Cho tam giác ABC có \(AB < AC,\) AD là đường phân giác. Khi đó:
Cho hình vẽ:
Chọn đáp án đúng
Cho tam giác ABC có \(AC = 2AB\) , AD là đường phân giác của góc BAC.
Chọn đáp án đúng
Cho hình vẽ sau:
Tỉ số diện tích tam giác ABD và tam giác ADC là:
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E.
Chọn đáp án đúng.
Cho tam giác ABC vuông tại A có \(AB = 4cm,BC = 5cm.\) Vẽ AD là phân giác của góc BAC. Tỉ số \(\frac{{DB}}{{DC}}\) là:
Cho tam giác ABC có \(BC = 10cm.\) Vẽ AD là tia phân giác của góc BAC sao cho \(BD = 4cm.\) Tỉ số \(\frac{{AB}}{{AC}}\) là:
Cho tam giác ABC vuông tại A, có \(AB = 3cm,AC = 4cm,AD\) là đường phân giác. Khoảng cách từ điểm D đến đường thẳng AC là:
: Cho tam giác ABC vuông tại A có \(AB = 15cm,AC = 20cm\) , đường cao AH (H thuộc BC). Tia phân giác của góc HAB cắt HB tại D. Tia phân giác của góc HAC cắt HC tại E. Độ dài đoạn thẳng DH bằng:
Cho tam giác ABC cân tại A, đường phân giác của góc ABC cắt AC tại D và \(AB = 15cm,BC = 10cm.\) Khi đó, độ dài đoạn thẳng AD bằng
Cho tam giác ABC có chu vi 27cm, các đường phân giác BD và CE. Biết rằng \(\frac{{AD}}{{DC}} = \frac{1}{2},\frac{{AE}}{{EB}} = \frac{3}{4}\) . Chọn đáp án đúng.
: Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Biết rằng \(AB = m,AC = n\left( {n > m} \right)\) . Diện tích tam giác ADM là:
Cho hình bình hành ABCD có \(AB = a = 12,5cm,BC = b = 7,25cm.\) Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F. Biết rằng \(FE = m = 3,45cm\) .
Chọn đáp án đúng
Cho tam giác ABC có \(AB = 4cm,AC = 5cm,BC = 6cm\) , các đường phân giác BD, CE cắt nhau tại I. Tỉ số diện tích của các tam giác ADE và ABC là:
Cho tam giác ABC có \(AB = 8cm,AC = 12cm,\) đường phân giác AD. Trên đoạn AD lấy điểm E sao cho \(\frac{{AE}}{{AD}} = \frac{3}{5}.\) Gọi K là giao điểm của BE và AC. Tính tỉ số \(\frac{{AK}}{{KC}}\)
