-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 4: Hàm số bậc hai
Bài 3 trang 39 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Vẽ đồ thị hàm số:
Đề bài
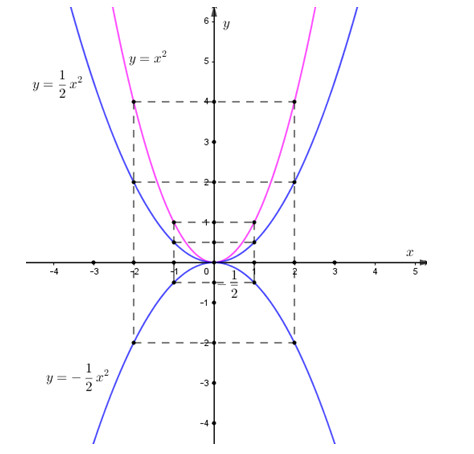
Vẽ đồ thị hàm số: \(y = {x^2},y = \dfrac{1}{2}{x^2},y = - \dfrac{1}{2}{x^2}.\)
Phương pháp giải - Xem chi tiết
Lập bảng 5 giá trị tương ứng của x, y thỏa mãn các hàm số và vẽ parabol đi qua các điểm đó.
Lời giải chi tiết
Vẽ đồ thị hàm số \(y = {x^2}\)
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = {x^2}\) |
\(4\) |
1 |
0 |
1 |
4 |
Vậy đồ thị hàm số \(y = {x^2}\) là parabol và đi qua các điểm có tọa độ là \(\left( { - 2;4} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1;1} \right);\left( {2;4} \right)\)
Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = \dfrac{1}{2}{x^2}\) |
\(2\) |
\(\dfrac{1}{2}\) |
0 |
\(\dfrac{1}{2}\) |
2 |
Vậy đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) là parabol và đi qua các điểm có tọa độ là \(\left( { - 2;2} \right);\left( { - 1;\dfrac{1}{2}} \right);\left( {0;0} \right);\left( {1;\dfrac{1}{2}} \right);\left( {2;2} \right)\)
Vẽ đồ thị hàm số \(y = - \dfrac{1}{2}{x^2}\)
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = - \dfrac{1}{2}{x^2}\) |
\( - 2\) |
\( - \dfrac{1}{2}\) |
0 |
\( - \dfrac{1}{2}\) |
\( - 2\) |
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}{x^2}\) là parabol và đi qua các điểm có tọa độ là \(\left( { - 2; - 2} \right);\left( { - 1; - \dfrac{1}{2}} \right);\left( {0;0} \right);\)\(\,\left( {1; - \dfrac{1}{2}} \right);\left( {2; - 2} \right)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4 trang 39 Tài liệu dạy – học Toán 9 tập 2
- Bài 5 trang 39 Tài liệu dạy – học Toán 9 tập 2
- Bài 6 trang 39 Tài liệu dạy – học Toán 9 tập 2
- Bài 7 trang 39 Tài liệu dạy – học Toán 9 tập 2
- Bài 8 trang 39 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
