 Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
 Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
Bài tập 24 trang 155 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho hình 51, biết
Đề bài
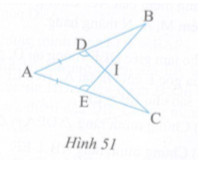
Cho hình 51, biết \(AD = AE,\,\,\widehat {ADC} = \widehat {AEB}.\)
a) Chứng minh rằng DC = EB.
b) Gọi I là giao điểm của BE và DC. Chứng minh rằng \(\Delta IDB = \Delta IEC\)
Lời giải chi tiết
a)Xét tam giác EAB và DAC có: \(\eqalign{ & \widehat {AEB} = \widehat {ADC}(gt) \cr & AE = AD(gt) \cr} \)
\(\widehat {EAB} = \widehat {DAC}\) (góc chung)
Do đó: \(\Delta EAB = \Delta DAC(g.c.g)\)
\(\Rightarrow EB = DC\) (2 cạnh tương ứng)
b)Ta có:
\(\eqalign{ & *\Delta EAB = \Delta DAC \Rightarrow AB = AC,\widehat {ABE} = \widehat {ACD} \cr & AD + BD = AB;AE + EC = AC \cr} \)
Mà AD = AE và AB = AC nên BD = EC.
\(*\widehat {BDI} + \widehat {ADI} = {180^0}\) (kề bù) và \(\widehat {CEI} + \widehat {IEA} = {180^0}\) (kề bù)
Mà \(\widehat {ADI} = \widehat {AEI}\) nên \(\widehat {BDI} = \widehat {CEI}\)
Xét tam giác DBI và ECI có: \(\eqalign{ & \widehat {IDB} = \widehat {IEC}(cmt) \cr & BD = CE(cmt) \cr & \widehat {DBI} = \widehat {ECI}(\widehat {ABE} = \widehat {ACD}) \cr} \)
Do đó: \(\Delta DBI = \Delta ECI(g.c.g)\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận