Trắc nghiệm Bài tập ôn tập chương 2 Toán 9
Đề bài
“Đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng ... và cắt trục tung tại điểm có tung độ bằng ...” . Trong dấu “…” lần lượt là?
-
A.
$\dfrac{b}{a};b$
-
B.
$\dfrac{{ - b}}{a};b$
-
C.
$\dfrac{b}{a}; - b$
-
D.
$ - \dfrac{b}{a}; - b$
Điểm nào sau đây thuộc ĐTHS $y = 2{\rm{x}} + 1$:
-
A.
$(0;1)$
-
B.
$(0; - 1)$
-
C.
$(1;0)$
-
D.
$( - 1;2)$
Với giá trị nào của $m$ thì điểm $\left( {1;2} \right)$ thuộc đường thẳng $x - y = m$?
-
A.
$ - 2$
-
B.
$2$
-
C.
$1$
-
D.
$ - 1$
Điểm $\left( { - 2;3} \right)$ thuộc đường thẳng nào trong các đường thẳng có phương trình sau:
-
A.
$3x - 2y = 3$
-
B.
$3x - y = 0$
-
C.
$0x + y = 3$
-
D.
$0x - 3y = 9$
Đồ thị hàm số $y = (3 - m)x + m + 3$ đi qua gốc tọa độ khi:
-
A.
$m = - 3$
-
B.
$m = 3$
-
C.
$m \ne 3$
-
D.
$m \ne \pm 3$
Cho $3$ đường thẳng $\left( d \right):{\rm{ }}y = \left( {m + 2} \right)x - 3m;\left( {d'} \right):{\rm{ }}y = 2x + 4\;;\left( {d''} \right):{\rm{ }}y = - 3x - 1.$ Giá trị của $m$ để $3$ đường thẳng trên đồng quy là :
-
A.
$ - 1$
-
B.
$1$
-
C.
$2$
-
D.
$ - 2$
Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:
-
A.
$1$
-
B.
$ - 3$
-
C.
$3$
-
D.
$ - 1$
Tìm $m$ để đường thẳng $\left( d \right):{\rm{ }}y = x + 3;\left( {d'} \right):{\rm{ }}y = - x + 1;\left( {d''} \right):{\rm{ }}y = \sqrt 3 x - m - 2$ đồng quy.
-
A.
$m = 4 + \sqrt 3 $
-
B.
$m = - 4 - \sqrt 3 $
-
C.
$m = 4 - \sqrt 3 $
-
D.
$m = 2 + \sqrt 3 $
Giá trị của $m$ để đường thẳng $y = (m - 1)x - m$ cắt trục tung tại điểm có tung độ là $1 + \sqrt 2 $ là:
-
A.
$ - 1 - \sqrt 2 $
-
B.
$1 + \sqrt 2 $
-
C.
$\sqrt 2 - 1$
-
D.
Đáp án khác
Hai đồ thị hàm số $y = \dfrac{1}{2}x - 3$ và $y = - x + 3$ cắt nhau tại điểm :
-
A.
$( - 4; - 1)$
-
B.
$( - 4;1)$
-
C.
$(4;1)$
-
D.
$(4; - 1)$
Cho $2$ đường thẳng: $d:y = - 4x + m + 1;d':y = \dfrac{4}{3}x + 15 - 3m$. Tìm giá trị của $m$ để $d$ cắt $d'$ tại điểm nằm trên trục tung.
-
A.
$m = - \dfrac{7}{2}$
-
B.
$m = 2$
-
C.
$m = 7$
-
D.
$m = \dfrac{7}{2}$
Cho $2$ đường thẳng $d:y = 2x - 1;d':y = (m - 3)x + 2$. Tìm $m$ để $d$ cắt $d'$ mà hoành độ và tung độ giao điểm cùng dấu.
-
A.
$\left\{ \begin{array}{l}m < 1\\m \ne - 5\end{array} \right.$
-
B.
$\left\{ \begin{array}{l}m > - 1\\m \ne 5\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}m < 5\\m > 1\end{array} \right.$
-
D.
$m>-1$
Tìm $m$ để đường thẳng $\left( d \right):{\rm{ 2}}y + x - 7 = 0;\left( {d'} \right):{\rm{ }}y = 3;\left( {d''} \right):{\rm{ }}y = mx - 1$ đồng quy.
-
A.
$m = - 4$
-
B.
$m = 3$
-
C.
$m = 4$
-
D.
Cả A và C đúng
Tìm $m$ để $2$ đường thẳng $d:y = 2x + m + 3;d':y = - 4x - m - 2$ cắt nhau tại $1$ điểm thuộc trục hoành.
-
A.
$m = - 4$
-
B.
$m = - 2$
-
C.
$m = 2$
-
D.
Đáp án khác
Cho đường thẳng $d:y = x - 1$. Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
-
A.
$2$
-
B.
$\sqrt 2 $
-
C.
$\dfrac{{\sqrt 2 }}{2}$
-
D.
\(\dfrac{{\sqrt 3 }}{2}\)
Cho đường thẳng $d$ vuông góc với $d':y = - \dfrac{1}{3}{\rm{x}}$ và $d$ đi qua $P\left( {1; - 1} \right)$ . Khi đó phương trình đường thẳng $d$ là:
-
A.
$y = 3x - 4$
-
B.
$y = 3x + 4$
-
C.
$y = 3x - 2$
-
D.
$y=3x+1$
Đường thẳng $y = a{\rm{x}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$ là:
-
A.
$y = - \dfrac{3}{4}x + \dfrac{1}{4}$
-
B.
$y = - \dfrac{3}{4}x - \dfrac{1}{4}$
-
C.
$y = - \dfrac{2}{3}x + \dfrac{1}{4}$
-
D.
$y = - \dfrac{3}{4}x + 1$
Cho đường thẳng $d':y = - 2x + 6$. Gọi $M,N$ lần lượt là giao điểm của $d'$ với $Ox$ và $Oy$. Khi đó chu vi tam giác $OMN$ là:
-
A.
$6 + 3\sqrt 5 $
-
B.
$9 + 3\sqrt 5 $
-
C.
$6$
-
D.
$9$
Cho $2$ đường thằng $d:y = 2x - 1;d':y = x - 3$. Đường thẳng nào đi qua giao điểm của $d$ và $d'$?
-
A.
$y = 3x + 1$
-
B.
$y = - x - 1$
-
C.
$y = - 3x - 3$
-
D.
$y = - \dfrac{1}{2}x + 3$
Đường thẳng $y = {\rm{ax}} + b$ đi qua điểm $\left( {3;2} \right)$. Khi đó $6a + 2b$ bằng:
-
A.
$2$
-
B.
$4$
-
C.
$ - 4$
-
D.
$6$
Biết đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành tại điểm có hoành độ bằng $1$ và cắt trục tung tại điểm có tung độ bằng $2.$ Giá trị của $a$ và $b$ lần lượt là:
-
A.
$\dfrac{1}{2};1$
-
B.
$1;1$
-
C.
$2; - 2$
-
D.
$ - 2;2$
Đường thẳng $d:y = {\rm{ax}} + b$ đi qua điểm $A\left( {2; - 1} \right)$ và $M$ . Biết $M$ thuộc đường thẳng $d':2x + y = 3$ và điểm $M$ có hoành độ bằng $0,5$ . Khi đó $a$ nhận giá trị là:
-
A.
$a = 1$
-
B.
$a = \pm 1$
-
C.
$a = - 1$
-
D.
$a=-2$
Tìm $m$ để giao điểm của $d:mx + 2y = 5;d':y = - 2x + 1$ nằm ở góc phần tư thứ nhất.
-
A.
$m = 10$
-
B.
$m < 10$
-
C.
$m > 10$
-
D.
$m = - 10$
Tìm $m$ để giao điểm của $d:y = 12x + 5 - m;d':y = 3x + m + 3$ nằm bên trái trục tung.
-
A.
$m < 1$
-
B.
$m = 1$
-
C.
$m > 1$
-
D.
$m > 2$
Cho đường thẳng ${d_1}:y = 2x + 6$ cắt $Ox;Oy$ theo thứ tự $A$ và $B$. Diện tích tam giác $OAB$ là:
-
A.
$9$
-
B.
$18$
-
C.
$12$
-
D.
$6$
Cho hàm số \(y = \left( {m + 1} \right)x + 6\,\,\,\left( 1 \right)\) với \(m \ne - 1\)
Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung.
-
A.
\(m = 2\)
-
B.
\(m = 4\)
-
C.
\(m = 8\)
-
D.
\(m = 0\)
Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:
-
A.
$\dfrac{{27}}{6}$ ( đvdt)
-
B.
$27$( đvdt)
-
C.
$\dfrac{{27}}{2}$ (đvdt)
-
D.
$\dfrac{{27}}{4}$(đvdt)
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \dfrac{1}{2}x + 2\)
Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
-
A.
\(m=1\)
-
B.
\(m=2\)
-
C.
\(m=3\)
-
D.
\(m=-1\)
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
-
A.
$y = - 2x + 3$
-
B.
$y = 2x + 3$
-
C.
$y = - 2x - 3$
-
D.
$y = 2x - 1$
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Viết phương trình đường trung trực của đoạn thẳng $AB$.
-
A.
$y = 0,5x + 0,5$
-
B.
$y = 0,5x - 1$
-
C.
$y = 2x - 0,5$
-
D.
$y = 0,5x - 0,5$
Cho hai đường thẳng \({d_1}:y = \left( {m - 2} \right)x + m + 4\) và \({d_2}:y = \left( {n + 1} \right)x - 3\)
Tìm điều kiện của \(m\) để hàm số có đồ thị \({d_1}\) luôn nghịch biến và điều kiện của \(n\) để hàm số có đồ thị \({d_2}\) luôn đồng biến.
-
A.
\(m > - 1\,\,;\,\,n < 2\)
-
B.
\(m < - 2\,\,;\,\,n > 1\)
-
C.
\(m < 2\,\,;\,\,\,n > - 1\)
-
D.
\(m > 1\,\,;\,\,\,n < - 2\)
Tìm các giá trị của \(m\) và của \(n\) để hai đường thẳng \({d_1}\)và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right).\)
-
A.
\(m = - 1;n = 2\)
-
B.
\(m = 1;n = - 2\)
-
C.
\(m = - 1;n = - 2\)
-
D.
\(m = 1;n = 2\)
Cho hai đường thẳng \(\left( d \right):y = \left( {m - 2} \right)x + m\) và \(\left( \Delta \right):y = - 4x + 1\)
Tìm \(m\) để \(\left( d \right)\) song song với \(\left( \Delta \right)\).
-
A.
\(m = 1\)
-
B.
\(m = - 1\)
-
C.
\(m = 2\)
-
D.
\(m = - 2\)
Tìm điểm cố định đường thẳng \(\left( d \right)\) luôn đi qua với mọi \(m\).
-
A.
\(A\left( { 1;2} \right)\)
-
B.
\(A\left( { - 1;2} \right)\)
-
C.
\(A\left( { 1;-2} \right)\)
-
D.
\(A\left( { - 1;-2} \right)\)
Tìm tọa độ điểm \(B\) thuộc \(\left( \Delta \right)\) sao cho \(AB\) vuông góc với \(\left( \Delta \right)\).
-
A.
\(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right).\)
-
B.
\(B\left( {\dfrac{{5}}{{17}};\dfrac{{37}}{{17}}} \right).\)
-
C.
\(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{-37}}{{17}}} \right).\)
-
D.
\(B\left( {\dfrac{{5}}{{17}};\dfrac{{-37}}{{17}}} \right).\)
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( {{d_m}} \right):y = mx - 2\)\(\left( {m \ne 0} \right)\)
Xác định \(m\) để hàm số \(y = mx - 2\)\(\left( {m \ne 0} \right)\) đồng biến.
-
A.
\(m > 0.\)
-
B.
\(m < 0.\)
-
C.
\(m > 1.\)
-
D.
\(0 < m < 1.\)
Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\)
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m = 3\)
-
D.
\(m = 4\)
Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng \(1.\)
-
A.
\(m = 1\) hoặc \(m = - 1\)
-
B.
\(m = 0\)
-
C.
\(m = 1\)
-
D.
\(m = 2\) hoặc \(m = - 2\)
Trong mặt phẳng tọa độ \(Oxy,\)cho hai đường thẳng \(\left( {{d_1}} \right):y = {m^2}x - {m^4} + 2\) và \(\left( {{d_2}} \right):y = \dfrac{{{m^2}}}{{{m^2} + 1}}x + 2\) (\(m\) là tham số thực khác 0). Tìm tất cả giá trị của tham số \(m\) để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm A duy nhất sao cho diện tích của hình thang \(ABHK\) bằng \(\dfrac{{15}}{2}.\) Biết \(B\left( { - 1;2} \right)\) và hai điểm \(H,K\) lần lượt là hình chiếu vuông góc của \(B\) và A lên trục hoành.
-
A.
\(m = \pm 1\)
-
B.
\(m = \pm 2\)
-
C.
\(m \ne 1\)
-
D.
\(m \ne 2\)
Lời giải và đáp án
“Đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng ... và cắt trục tung tại điểm có tung độ bằng ...” . Trong dấu “…” lần lượt là?
-
A.
$\dfrac{b}{a};b$
-
B.
$\dfrac{{ - b}}{a};b$
-
C.
$\dfrac{b}{a}; - b$
-
D.
$ - \dfrac{b}{a}; - b$
Đáp án : B
- ĐTHS cắt trục hoành thì cho $y=0$ từ đó tìm được $x,$ ĐTHS cắt trục tung thì cho $x=0$ từ đó tìm được $y.$
- So sánh với đề bài để tìm ra biểu thức cần điền vào chỗ trống.
Đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành $ \Rightarrow y = 0 \Rightarrow {\rm{ax}} + b = 0 \Leftrightarrow x = - \dfrac{b}{a}$
ĐTHS $y = {\rm{ax}} + b$ cắt trục tung $ \Rightarrow x = 0 \Rightarrow y = {\rm{a}}{\rm{.0}} + b \Rightarrow y = b$
Vậy đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng $-\dfrac{b}{a}$ và cắt trục tung tại điểm có tung độ bằng $b$.
Điểm nào sau đây thuộc ĐTHS $y = 2{\rm{x}} + 1$:
-
A.
$(0;1)$
-
B.
$(0; - 1)$
-
C.
$(1;0)$
-
D.
$( - 1;2)$
Đáp án : A
Sử dụng kiến thức: Điểm $({x_0};{y_0})$ thuộc ĐTHS $y = {\rm{ax}} + b \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
Đáp án A: Thay $ x_0=0;y_0=1$ vào hàm số, ta có $ 2.0 + 1 = 1 \Rightarrow (0;1)$ thuộc ĐTHS đã cho.
Với giá trị nào của $m$ thì điểm $\left( {1;2} \right)$ thuộc đường thẳng $x - y = m$?
-
A.
$ - 2$
-
B.
$2$
-
C.
$1$
-
D.
$ - 1$
Đáp án : D
Điểm $({x_0};{y_0})$ thuộc ĐTHS $y = {\rm{ax}} + b \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
Điểm $(1;2)$ thuộc ĐTHS $x - y = m \Leftrightarrow 1 - 2 = m \Leftrightarrow - 1 = m$.
Điểm $\left( { - 2;3} \right)$ thuộc đường thẳng nào trong các đường thẳng có phương trình sau:
-
A.
$3x - 2y = 3$
-
B.
$3x - y = 0$
-
C.
$0x + y = 3$
-
D.
$0x - 3y = 9$
Đáp án : C
- Điểm $({x_0};{y_0})$ thuộc ĐTHS $y = {\rm{ax}} + b \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
- Tính toán và chọn đáp án phù hợp.
Ta có $3( - 2) - 2.3 = - 12 \ne 3$=> loại A
$3( - 2) - 3 = - 9 \ne 0$ => loại B
$0( - 2) + 3 = 3$
Đồ thị hàm số $y = (3 - m)x + m + 3$ đi qua gốc tọa độ khi:
-
A.
$m = - 3$
-
B.
$m = 3$
-
C.
$m \ne 3$
-
D.
$m \ne \pm 3$
Đáp án : A
Sử dụng kiến thức: Điểm thuộc đồ thị hàm số.
Điểm $M(x_0;y_0)$ thuộc đồ thị hàm số $y=ax+b$ \( \Leftrightarrow {y_0} = a{x_0} + b\)
Ta có điểm $O\left( {0\;;0} \right)$ thuộc đường thẳng $y = (3 - m)x + m + 3 \Leftrightarrow (3-m).0+m + 3 = 0 $$\Leftrightarrow m+3=0\Leftrightarrow m = - 3$
Cho $3$ đường thẳng $\left( d \right):{\rm{ }}y = \left( {m + 2} \right)x - 3m;\left( {d'} \right):{\rm{ }}y = 2x + 4\;;\left( {d''} \right):{\rm{ }}y = - 3x - 1.$ Giá trị của $m$ để $3$ đường thẳng trên đồng quy là :
-
A.
$ - 1$
-
B.
$1$
-
C.
$2$
-
D.
$ - 2$
Đáp án : A
- Tìm tọa độ giao điểm 2 đường thẳng cho trước $d';d''$
- Cho giao điểm vừa tìm được thuộc vào đường thẳng $d$.
Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đường thẳng \(\left( d \right):y = ax + b \)\(\Leftrightarrow {y_0} = a{x_0} + b\)
Xét phương trình hoành độ giao điểm $A$ của $\left( {d'} \right)$ và $\left( {d''} \right)$:
$\begin{array}{*{20}{l}}{2x + 4 = - 3x - 1}\\{ \Leftrightarrow 5x = - 5}\\{ \Leftrightarrow x = - 1}\\{ \Rightarrow y = 2\left( { - 1} \right) + 4 = 2}\\{ \Rightarrow A\left( { - 1;2} \right)}\end{array}$
Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy thì $A\left( { - 1;2} \right) \in \left( d \right)$
$\begin{array}{*{20}{l}}{ \Leftrightarrow 2 = \left( {m + 2} \right).\left( { - 1} \right) - 3m}\\{ \Leftrightarrow 2 = - 2 - 4m}\\{ \Leftrightarrow 4m = - 4}\\{ \Leftrightarrow m = - 1}\end{array}$
Vậy khi $m = - 1$ thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy tại $A\left( { - 1;2} \right)$.
Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:
-
A.
$1$
-
B.
$ - 3$
-
C.
$3$
-
D.
$ - 1$
Đáp án : A
- Viết phương trình đường thẳng $(d)$ đi qua 2 điểm cho trước $A;B$.
- Để $3$ điểm $A;B;C$ thẳng hàng thì $C \in (d)$
Gọi $d:y = {\rm{ax}} + b$ là đường thẳng đi qua $A$ và $B$.
$\begin{array}{l}A(0;3) \in d \Leftrightarrow a.0 + b = 3 \Leftrightarrow b = 3\\B(2;2) \in d \Leftrightarrow a.2 + b = 2\\ \Rightarrow \left\{ \begin{array}{l}b = 3\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = - \dfrac{1}{2}\end{array} \right. \Rightarrow d:y = - \dfrac{1}{2}x + 3\end{array}$
Để $3$ điểm $A,B,C$ thẳng hàng thì $C(m + 3;m) \in (d):y = - \dfrac{1}{2}x + 3$
$ \Leftrightarrow m = - \dfrac{1}{2}\left( {m + 3} \right) + 3 \Leftrightarrow \dfrac{3}{2}m = \dfrac{3}{2} \Leftrightarrow m = 1$.
Vậy $m = 1$.
Tìm $m$ để đường thẳng $\left( d \right):{\rm{ }}y = x + 3;\left( {d'} \right):{\rm{ }}y = - x + 1;\left( {d''} \right):{\rm{ }}y = \sqrt 3 x - m - 2$ đồng quy.
-
A.
$m = 4 + \sqrt 3 $
-
B.
$m = - 4 - \sqrt 3 $
-
C.
$m = 4 - \sqrt 3 $
-
D.
$m = 2 + \sqrt 3 $
Đáp án : B
- Tìm tọa độ giao điểm 2 đường thẳng cho trước $d;d'$
- Cho giao điểm vừa tìm được thuộc vào đường thẳng $d''$.
Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đường thẳng \(\left( d \right):y = ax + b \)\(\Leftrightarrow {y_0} = a{x_0} + b\)
$d:y = x + 3;d':y = - x + 1;d'':y = \sqrt 3 x - m - 2$
Xét phương trình hoành độ giao điểm của $d$ và $d'$: $x + 3 = - x + 1 \Leftrightarrow 2x = - 2 \Leftrightarrow x = - 1 \Rightarrow y = 2$
Do đó $d$ và $d'$ cắt nhau tại điểm $\left( { - 1;2} \right)$.
Điểm $A( - 1;2) \in d'':y = \sqrt 3 x - m - 2 $$\Leftrightarrow 2 = \sqrt 3 .\left( { - 1} \right) - m - 2 $$\Leftrightarrow m = - 4 - \sqrt 3 $
Vậy $m = - 4 - \sqrt 3 $.
Giá trị của $m$ để đường thẳng $y = (m - 1)x - m$ cắt trục tung tại điểm có tung độ là $1 + \sqrt 2 $ là:
-
A.
$ - 1 - \sqrt 2 $
-
B.
$1 + \sqrt 2 $
-
C.
$\sqrt 2 - 1$
-
D.
Đáp án khác
Đáp án : A
Sử dụng kiến thức đồ thị hàm số $y=ax+b$ cắt trục $Oy$ tại điểm $(0;b)$ và tính toán.
Đồ thị hàm số $y = (m - 1)x - m$ cắt trục tung tại điểm có tung độ là $1 + \sqrt 2 $
$ \Rightarrow - m = 1 + \sqrt 2 \Rightarrow m = - 1 - \sqrt 2 $
Học sinh cần chú ý quy tắc đổi dấu khi bỏ hoặc thêm dấu ngoặc đằng trước có dấu trừ.
Hai đồ thị hàm số $y = \dfrac{1}{2}x - 3$ và $y = - x + 3$ cắt nhau tại điểm :
-
A.
$( - 4; - 1)$
-
B.
$( - 4;1)$
-
C.
$(4;1)$
-
D.
$(4; - 1)$
Đáp án : D
Xét phương trình hoành độ giao điểm 2 đường thẳng để tìm $x$ từ đó ta tìm được $y$.
Xét phương trình hoành độ giao điểm:
$\begin{array}{l}\dfrac{1}{2}x - 3 = - x + 3 \Leftrightarrow \dfrac{3}{2}x = 6 \Leftrightarrow x = 4\\ \Rightarrow y = - 4 + 3 = - 1.\end{array}$
Vậy giao điểm cần tìm có tọa độ $(-4;1)$.
Cho $2$ đường thẳng: $d:y = - 4x + m + 1;d':y = \dfrac{4}{3}x + 15 - 3m$. Tìm giá trị của $m$ để $d$ cắt $d'$ tại điểm nằm trên trục tung.
-
A.
$m = - \dfrac{7}{2}$
-
B.
$m = 2$
-
C.
$m = 7$
-
D.
$m = \dfrac{7}{2}$
Đáp án : D
- Tìm tọa độ giao điểm hai đường thẳng cho trước
- Một điểm nằm trên trục tung khi và chỉ khi hoành độ bằng $0.$
Xét phương trình hoành độ giao điểm của $d$ và $d'$ :
$ - 4x + m + 1 = \dfrac{4}{3}x + 15 - 3m \Leftrightarrow \dfrac{{ - 16}}{3}x = 14 - 4m \Leftrightarrow x = \dfrac{{3(4m - 14)}}{{16}}$
$d$ cắt $d'$ tại điểm nằm trên trục tung $ \Leftrightarrow x = \dfrac{{3(4m - 14)}}{{16}} = 0 \Leftrightarrow 4m - 14 = 0 \Leftrightarrow m = \dfrac{7}{2}.$
Cho $2$ đường thẳng $d:y = 2x - 1;d':y = (m - 3)x + 2$. Tìm $m$ để $d$ cắt $d'$ mà hoành độ và tung độ giao điểm cùng dấu.
-
A.
$\left\{ \begin{array}{l}m < 1\\m \ne - 5\end{array} \right.$
-
B.
$\left\{ \begin{array}{l}m > - 1\\m \ne 5\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}m < 5\\m > 1\end{array} \right.$
-
D.
$m>-1$
Đáp án : B
- Tìm tọa độ giao điểm 2 đường thẳng cho trước
- Hoành độ và tung độ giao điểm cùng dấu $ \Leftrightarrow xy > 0$.
Ta có $d \cap d' \Leftrightarrow m - 3 \ne 2 \Leftrightarrow m \ne 5$.
Xét phương trình hoành độ của $d'$ và $d''$ :
$\begin{array}{l}2x - 1 = (m - 3)x + 2 \Leftrightarrow (m - 5)x = - 3 \Leftrightarrow x = \dfrac{{ - 3}}{{m - 5}}\\ \Rightarrow y = \dfrac{{ - 6}}{{m - 5}} - 1 = \dfrac{{ - m - 1}}{{m - 5}}\end{array}$
Theo đề bài: $x.y > 0 \Leftrightarrow \dfrac{{ - 3}}{{m - 5}}.\dfrac{{ - m - 1}}{{m - 5}} > 0 \Leftrightarrow \dfrac{{3(m + 1)}}{{{{(m - 5)}^2}}} > 0$
Mà ${(m - 5)^2} > 0,\forall m \ne 5$
Suy ra $m > - 1$
Kết hợp điều kiện ta có: $\left\{ \begin{array}{l}m > - 1\\m \ne 5\end{array} \right.$.
Tìm $m$ để đường thẳng $\left( d \right):{\rm{ 2}}y + x - 7 = 0;\left( {d'} \right):{\rm{ }}y = 3;\left( {d''} \right):{\rm{ }}y = mx - 1$ đồng quy.
-
A.
$m = - 4$
-
B.
$m = 3$
-
C.
$m = 4$
-
D.
Cả A và C đúng
Đáp án : C
- Tìm tọa độ giao điểm 2 đường thẳng cho trước $d;d'$
- Cho giao điểm vừa tìm được thuộc vào đường thẳng $d''$.
Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đường thẳng \(\left( d \right):y = ax + b \)\(\Leftrightarrow {y_0} = a{x_0} + b\)
$\left( d \right):{\rm{ 2}}y + x - 7 = 0 \Leftrightarrow y = - \dfrac{1}{2}x + \dfrac{7}{2}$
Xét phương trình hoành độ giao điểm của $\left( {d'} \right)$ và $\left( {d''} \right)$ : $ - \dfrac{1}{2}x + \dfrac{7}{2} = 3 \Leftrightarrow - \dfrac{1}{2}x = - \dfrac{1}{2} \Leftrightarrow x = 1$ nên tọa độ giao điểm là $(1;3)$
Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy thì $\left( {1;3} \right) \in \left( {d''} \right) \Leftrightarrow 3 = 1.m - 1 \Leftrightarrow m = 4$
Vậy với $m = 4$ thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy.
Tìm $m$ để $2$ đường thẳng $d:y = 2x + m + 3;d':y = - 4x - m - 2$ cắt nhau tại $1$ điểm thuộc trục hoành.
-
A.
$m = - 4$
-
B.
$m = - 2$
-
C.
$m = 2$
-
D.
Đáp án khác
Đáp án : A
- Tìm tọa độ giao điểm 2 đường thẳng
- Điểm thuộc trục hoành khi và chỉ khi tung độ bằng 0.
Xét phương trình hoành độ giao điểm của $d$ và $d'$:
$2x + m + 3 = - 4x - m - 2 \Leftrightarrow 6x = - 2m - 5 $$\Leftrightarrow x = \dfrac{{ - 2m - 5}}{6}$
$ \Rightarrow y = 2.\dfrac{{ - 2m - 5}}{6} + m + 3 $$= \dfrac{{m + 4}}{3}$
Ta có $d$ cắt $d'$ tại điểm thuộc trục hoành nên: $y = \dfrac{{m + 4}}{3} = 0 \Leftrightarrow m = - 4.$
Vậy $m = - 4$.
Cho đường thẳng $d:y = x - 1$. Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
-
A.
$2$
-
B.
$\sqrt 2 $
-
C.
$\dfrac{{\sqrt 2 }}{2}$
-
D.
\(\dfrac{{\sqrt 3 }}{2}\)
Đáp án : C
- Tìm giao điểm của đường thẳng với trục hoành, trục tung
- Dựng hình chiếu của tam giác được tạo thành
- Áp dụng hệ thức trong tam giác vuông để tính khoảng cách từ điểm $O$ đến $1$ đường thẳng.
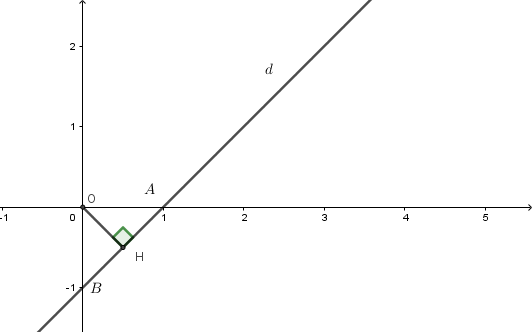
Ta có:
$d \cap Ox$ tại $A(1;0) \Rightarrow OA = 1$
$d \cap Oy $ tại $ B(0; - 1) \Rightarrow OB = 1$
Ta có $OA \bot OB$. Gọi $H$ là hình chiếu của $O$ trên đường thẳng $AB$.
Áp dụng hệ thức trong tam giác ta có:
$\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{1} + \dfrac{1}{1} = 2\\ \Rightarrow OH = \dfrac{{\sqrt 2 }}{2}\end{array}$
HS dễ mắc phải một số sai lầm sau:
- Học sinh hay xác định nhầm giao điểm của đường thẳng với trục hoành, trục tung.
- Học sinh không khai căn để được kết quả cuối cùng.
Cho đường thẳng $d$ vuông góc với $d':y = - \dfrac{1}{3}{\rm{x}}$ và $d$ đi qua $P\left( {1; - 1} \right)$ . Khi đó phương trình đường thẳng $d$ là:
-
A.
$y = 3x - 4$
-
B.
$y = 3x + 4$
-
C.
$y = 3x - 2$
-
D.
$y=3x+1$
Đáp án : A
Sử dụng kiến thức:
+) $d \bot d' \Leftrightarrow a.a' = - 1$
+) Điểm $({x_0};{y_0})$ thuộc đồ thị hàm số $y = {\rm{ax}} + b $$\Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
Đường thẳng $d$ vuông góc với đường thẳng $d' \Rightarrow a.\dfrac{{ - 1}}{3} = - 1 \Leftrightarrow a = 3$
Đường thẳng $d$ đi qua điểm $P(1;-1) \Rightarrow 3.1 + b = - 1 \Leftrightarrow b = - 4$
$ \Rightarrow d:y = 3x - 4$.
Đường thẳng $y = a{\rm{x}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$ là:
-
A.
$y = - \dfrac{3}{4}x + \dfrac{1}{4}$
-
B.
$y = - \dfrac{3}{4}x - \dfrac{1}{4}$
-
C.
$y = - \dfrac{2}{3}x + \dfrac{1}{4}$
-
D.
$y = - \dfrac{3}{4}x + 1$
Đáp án : B
Sử dụng kiến thức:
+) Điểm $({x_0};{y_0})$ thuộc đồ thị hàm số $y = {\rm{ax}} + b$$ \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
+) Từ đó tìm $a;b$.
Gọi $d:y = {\rm{ax}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$
$M$ thuộc $d \Leftrightarrow - 3a + b = 2 \Rightarrow b = 2 + 3a\,\,\,\,\,(1)$
$N$ thuộc $d \Leftrightarrow 1.a + b = - 1 \Rightarrow b = - 1 - a \,\,\,\,\,(2)$
Từ (1) và (2) suy ra \(2 + 3a = - 1 - a \Leftrightarrow 4a = - 3 \Leftrightarrow a = - \dfrac{3}{4}\)\( \Rightarrow b = 2 + 3a = - \dfrac{1}{4}\)
Nên $a = \dfrac{{ - 3}}{4};b = - \dfrac{1}{4}$.
Vậy $d:y = - \dfrac{3}{4}x - \dfrac{1}{4}$.
Cho đường thẳng $d':y = - 2x + 6$. Gọi $M,N$ lần lượt là giao điểm của $d'$ với $Ox$ và $Oy$. Khi đó chu vi tam giác $OMN$ là:
-
A.
$6 + 3\sqrt 5 $
-
B.
$9 + 3\sqrt 5 $
-
C.
$6$
-
D.
$9$
Đáp án : B
- Tìm giao điểm của đường thẳng với trục hoành, trục tung
- Áp dụng định lý Py-ta-go để tính độ dài đoạn thẳng.
- Sử dụng công thức chu vi tam giác.
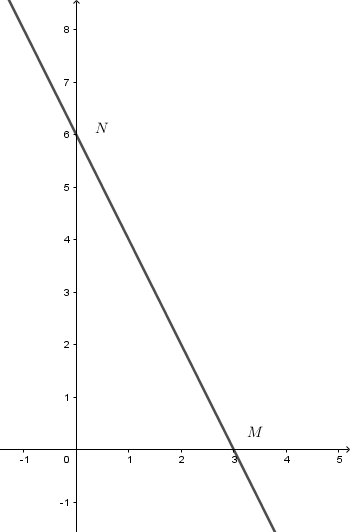
Ta có:
$\begin{array}{l}d' \cap Ox = M(3;0) \Rightarrow OM = 3\\d' \cap Oy = N(0;6) \Rightarrow ON = 6\end{array}$
Ta có tam giác $OMN$ vuông tại $O$.
Áp dụng định lý Py ta go ta có:
$M{N^2} = O{M^2} + O{N^2} = 9 + 36 = 45 \Rightarrow MN = 3\sqrt 5 $
Suy ra chu vi tam giác $OMN$ là: $MN + OM + ON = 3\sqrt 5 + 3 + 6 = 9 + 3\sqrt 5 $
Cho $2$ đường thằng $d:y = 2x - 1;d':y = x - 3$. Đường thẳng nào đi qua giao điểm của $d$ và $d'$?
-
A.
$y = 3x + 1$
-
B.
$y = - x - 1$
-
C.
$y = - 3x - 3$
-
D.
$y = - \dfrac{1}{2}x + 3$
Đáp án : A
Sử dụng kiến thức:
- Xác định giao điểm của $2$ đường thẳng
- Cho giao điểm đó thuộc đường thẳng ở các phương án để tìm ra đáp án phù hợp.
Xét phương trình hoành độ giao điểm của $d$ và $d'$ ta có
$2x - 1 = x - 3 \Leftrightarrow x = - 2 \Rightarrow y = - 5 \Rightarrow M( - 2; - 5)$
Trước hết xét $M$ có thuộc đường thẳng $y = 3x + 1$ không?
Ta có $3.{x_M} + 1 = 3.( - 2) + 1 = - 5 = {y_M}$ nên $M$ thuộc đồ thị hàm số $y=3x+1$ hay A đúng.
Đường thẳng $y = {\rm{ax}} + b$ đi qua điểm $\left( {3;2} \right)$. Khi đó $6a + 2b$ bằng:
-
A.
$2$
-
B.
$4$
-
C.
$ - 4$
-
D.
$6$
Đáp án : B
- Sử dụng kiến thức:
Điểm $M(x_0;y_0)$ thuộc đồ thị hàm số $y=ax+b$ $\Leftrightarrow {y_0} = a{x_0} + b$
- Biến đổi biểu thức cần tính để xuất hiện biểu thức đã có ở bước trên
Điểm $\left( {3;2} \right)$ thuộc đường thẳng $y = {\rm{a}}x + b \Rightarrow 3a + b = 2$
Ta có $6a + 2b = 2(3a + b) = 2.2 = 4$
Biết đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành tại điểm có hoành độ bằng $1$ và cắt trục tung tại điểm có tung độ bằng $2.$ Giá trị của $a$ và $b$ lần lượt là:
-
A.
$\dfrac{1}{2};1$
-
B.
$1;1$
-
C.
$2; - 2$
-
D.
$ - 2;2$
Đáp án : D
Sử dụng kiến thức:
- Đường thẳng $y=ax+b$ $(a \ne 0)$ cắt trục hoành tại điểm có hoành độ $x=\dfrac{-b}{a}$ và cắt trục tung tại điểm có tung độ $y=b$
- Biến đổi để tìm $a;b.$
Đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành tại điểm có hoành độ bằng $1$ và cắt trục tung tại điểm có tung độ bằng $2$
$ \Rightarrow \left\{ \begin{array}{l}1.a + b = 0\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 2\end{array} \right.$
Đường thẳng $d:y = {\rm{ax}} + b$ đi qua điểm $A\left( {2; - 1} \right)$ và $M$ . Biết $M$ thuộc đường thẳng $d':2x + y = 3$ và điểm $M$ có hoành độ bằng $0,5$ . Khi đó $a$ nhận giá trị là:
-
A.
$a = 1$
-
B.
$a = \pm 1$
-
C.
$a = - 1$
-
D.
$a=-2$
Đáp án : D
Ta sử dụng
Điểm $M(x_0;y_0)$ thuộc đồ thị hàm số $y=ax+b$ $\Leftrightarrow {y_0} = a{x_0} + b$
Điểm \(A\left( {2; - 1} \right) \in d:y = ax + b \Leftrightarrow 2a + b = - 1\)
Điểm \(M \in d':2x + y = 3\) có \(x = 0,5 \Rightarrow 2.0,5 + y = 3 \Leftrightarrow y = 2 \Rightarrow M\left( {\dfrac{1}{2};2} \right)\).
\(M\left( {\dfrac{1}{2};2} \right) \in d \Leftrightarrow \dfrac{1}{2}a + b = 2\)
Do đó \(\left\{ \begin{array}{l}2a + b = - 1\\\dfrac{1}{2}a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} b = - 1-2a\\b = 2-\dfrac{1}{2}a\end{array} \right. \)\(\Rightarrow - 1 - 2a = 2 - \dfrac{1}{2}a \Leftrightarrow \dfrac{3}{2}a = - 3 \Leftrightarrow a = - 2\)
Vậy \(a = - 2\).
Tìm $m$ để giao điểm của $d:mx + 2y = 5;d':y = - 2x + 1$ nằm ở góc phần tư thứ nhất.
-
A.
$m = 10$
-
B.
$m < 10$
-
C.
$m > 10$
-
D.
$m = - 10$
Đáp án : C
Sử dụng kiến thức:
- Điều kiện để 2 đường thẳng cắt nhau
- Tìm giao điểm 2 đường thẳng
- Điểm thuộc góc phần tư thứ nhất khi và chỉ khi $x > 0$ và $y > 0$
$\begin{array}{l}d:mx + 2y = 5 \Rightarrow y = \dfrac{{ - m}}{2}x + \dfrac{5}{2}\\d \cap d' \Leftrightarrow - \dfrac{m}{2} \ne - 2 \Leftrightarrow m \ne 4.\end{array}$
Xét phương trình hoành độ giao điểm của $d$ và $d'$ :
$\dfrac{{ - m}}{2}x + \dfrac{5}{2} = - 2x + 1 \Leftrightarrow \dfrac{{4 - m}}{2}x = - \dfrac{3}{2} $$\Leftrightarrow x = \dfrac{3}{{m - 4}} \Rightarrow y=-2.\dfrac{3}{{m - 4}}-1 = \dfrac{{m - 10}}{{m - 4}}$
Do $d$ cắt $d'$ tại điểm nằm ở góc phần tư thứ nhất nên ta có: $\left\{ \begin{array}{l}x > 0\\y > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{{m - 4}} > 0\\\dfrac{{m - 10}}{{m - 4}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 4\\m > 10\end{array} \right. \Leftrightarrow m > 10$
Kết hợp điều kiện suy ra $m > 10$ thỏa mãn yêu cầu đề bài.
Tìm $m$ để giao điểm của $d:y = 12x + 5 - m;d':y = 3x + m + 3$ nằm bên trái trục tung.
-
A.
$m < 1$
-
B.
$m = 1$
-
C.
$m > 1$
-
D.
$m > 2$
Đáp án : A
Sử dụng kiến thức
- Tìm tọa độ giao điểm 2 đường thẳng
- Điểm nằm bên trái trục tung khi và chỉ khi $x < 0$
Xét phương trình hoành độ giao điểm của $d$ và $d'$ : $12x + 5 - m = 3x + m + 3 \Leftrightarrow 9x = 2m - 2 \Leftrightarrow x = \dfrac{{2m - 2}}{9}$
Do $d$ cắt $d'$ tại điểm nằm bên trái trục tung nên ta có: $x < 0 \Leftrightarrow \dfrac{{2m - 2}}{9} < 0 \Leftrightarrow 2m - 2 < 0 \Leftrightarrow m < 1.$
Cho đường thẳng ${d_1}:y = 2x + 6$ cắt $Ox;Oy$ theo thứ tự $A$ và $B$. Diện tích tam giác $OAB$ là:
-
A.
$9$
-
B.
$18$
-
C.
$12$
-
D.
$6$
Đáp án : A
- Tìm giao điểm của đường thẳng với $2$ trục tọa độ.
- Tính độ dài đoạn thẳng
- Sử dụng công thức tính diện tích tam giác vuông
Ta có:
$d \cap Ox $ tại $A( - 3;0) \Rightarrow OA = 3$
$d \cap Oy $ tại $B(0;6) \Rightarrow OB = 6$
Ta có $OA \bot OB$.
Diện tích tam giác $AOB$ là: $\dfrac{1}{2}.3.6 = 9(đv{\rm{d}}t)$
- Học sinh tính nhầm giao điểm.
- Khi tính diện tích tam giác học sinh quên không chia $2$ dẫn đến kết quả sai.
Cho hàm số \(y = \left( {m + 1} \right)x + 6\,\,\,\left( 1 \right)\) với \(m \ne - 1\)
Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung.
-
A.
\(m = 2\)
-
B.
\(m = 4\)
-
C.
\(m = 8\)
-
D.
\(m = 0\)
Đáp án : C
Để hai đường thẳng \(\left( d \right):y = ax + b\) và \(\left( {d'} \right):y = a'x + b'\) cắt nhau tại một điểm trên trục tung thì \(a \ne a'\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\).
Để \(d:\,\,y = \left( {m + 1} \right)x + 6\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung thì \(m + 1 \ne 5\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 5\\\left( {m + 1} \right).0 + 6 = 5.0 + m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\6 = m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m = 8\end{array} \right. \Leftrightarrow m = 8\,\,\,\left( {tmđk\,\,m \ne - 1} \right)\end{array}\)
Vậy \(m = 8\) là giá trị cần tìm.
Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:
-
A.
$\dfrac{{27}}{6}$ ( đvdt)
-
B.
$27$( đvdt)
-
C.
$\dfrac{{27}}{2}$ (đvdt)
-
D.
$\dfrac{{27}}{4}$(đvdt)
Đáp án : D
- Xác định giao điểm 2 đường thẳng đã cho
- Dựng đường cao của tam giác được tạo thành
- Tính độ dài các đoạn thẳng
- Tính diện tích tam giác.
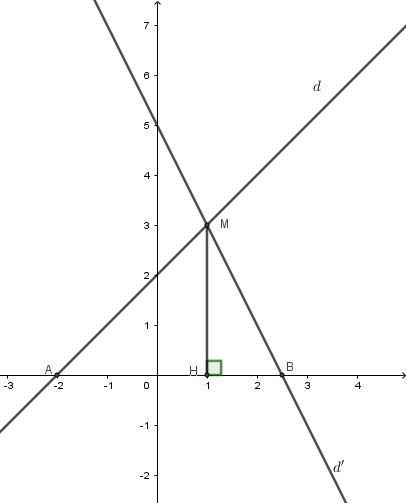
Xét phương trình hoành độ giao điểm của ${d_1};{d_2}$
$x + 2 = - 2x + 5 \Leftrightarrow x = 1 \Rightarrow y = 3 \Rightarrow {d_1} \cap {d_2}$ tại $ M(1;3)$
Gọi $H$ là chân đường vuông góc kẻ từ $M$ tới $Ox$. Suy ra $MH = 3$
$d \cap Ox$ tại $ A( - 2;0) \Rightarrow OA = 2$
$d' \cap Ox$ tại $ B\left( {\dfrac{5}{2};0} \right) \Rightarrow OB = \dfrac{5}{2}$
$\Rightarrow AB = OA+OB=2 + \dfrac{5}{2} = \dfrac{9}{2}$
${S_{MAB}} = \dfrac{1}{2}AB.MH = \dfrac{1}{2}.\dfrac{9}{2}.3 = \dfrac{{27}}{4}\,(dvdt)$
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \dfrac{1}{2}x + 2\)
Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
-
A.
\(m=1\)
-
B.
\(m=2\)
-
C.
\(m=3\)
-
D.
\(m=-1\)
Đáp án : A
Xét phương trình hoành độ giao điểm của hai đồ thị \((d_1);(d_2)\) để tìm \(x,\) thay giá trị \(x\) vừa tìm được vào 1 trong hai phương trình để tìm \(y.\)
Ba đường thẳng đồng quy khi và chỉ khi đường thẳng thứ ba đi qua giao điểm của hai đường thẳng còn lại.
Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):
\(2x - 3 = - \dfrac{1}{2}x + 2 \Leftrightarrow 2x + \dfrac{1}{2}x = 2 + 3 \Leftrightarrow \dfrac{5}{2}x = 5 \Leftrightarrow x = 2\)
Thay \(x = 2\) vào hàm số \(y = 2x - 3\) ta được \(y = 2.2 - 3 = 1.\)
Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(A\left( {2;1} \right)\).
Ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy \( \Rightarrow \left( {{d_3}} \right)\) đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)\( \Rightarrow A \in \left( {{d_3}} \right)\)
Thay tọa độ điểm \(A\) vào hàm số \(\left( {{d_3}} \right):\,\,y = 3x - 2m - 3\) ta được:
\(1 = 3.2 - 2m - 3\)\( \Rightarrow 2m = 6 - 3 - 1 \Rightarrow m = 1\)
Vậy \(m = 1\) thì ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
-
A.
$y = - 2x + 3$
-
B.
$y = 2x + 3$
-
C.
$y = - 2x - 3$
-
D.
$y = 2x - 1$
Đáp án : C
- Viết phương trình đường thẳng đi qua 2 điểm cho trước
- Nhận xét được $MN//AB$ và $AB$ đi qua trung điểm $P$
Giả sử $MN:y = {\rm{ax}} + b$
Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$;
$M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$ $\Rightarrow b=2$
Do đó $MN:y = - 2{\rm{x}} + 2$.
Vì $M,N$ lần lượt là trung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$
Suy ra $AB$ có dạng: $y = - 2x + b'\,(b' \ne 2)$
Vì $P$ là trung điểm của $AB$ nên $AB$ đi qua $P\left( { - 1; - 1} \right)$
$ \Rightarrow - 1 = - 2( - 1) + b' \Leftrightarrow b' = - 3(t/m)$
Vậy $AB:y = - 2x - 3.$
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Viết phương trình đường trung trực của đoạn thẳng $AB$.
-
A.
$y = 0,5x + 0,5$
-
B.
$y = 0,5x - 1$
-
C.
$y = 2x - 0,5$
-
D.
$y = 0,5x - 0,5$
Đáp án : D
- Sử dụng kiến thức đường trung bình của tam giác
- Điểm thuộc đường thẳng
- Hai đường thẳng vuông góc: $ d \bot d'$ \( \Leftrightarrow a.a' = - 1\) \( (a;a' \ne 0) \)
Gọi phương trình đường trung trực của $AB$ là $d:y = mx + n$ và $MN:y = ax + b$
Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$;
$M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$
Do đó $MN:y = - 2{\rm{x}} + 2$.
Vì $M,N$ lần lượt là trung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$.
Vì $d$ là đường trung trực của $AB$ nên $BC \bot MN \Rightarrow m( - 2) = - 1 \Leftrightarrow m = \dfrac{1}{2}$
$ \Rightarrow d:y = \dfrac{1}{2}x + n$
Vì $P$ là trung điểm của $AB$ nên \(d\) đi qua $P$
$ \Rightarrow - 1 = \dfrac{1}{2}( - 1) + n \Leftrightarrow n = - \dfrac{1}{2}$.
Vậy trung trực của $AB$ là : $y = \dfrac{1}{2}x - \dfrac{1}{2}$.
Cho hai đường thẳng \({d_1}:y = \left( {m - 2} \right)x + m + 4\) và \({d_2}:y = \left( {n + 1} \right)x - 3\)
Tìm điều kiện của \(m\) để hàm số có đồ thị \({d_1}\) luôn nghịch biến và điều kiện của \(n\) để hàm số có đồ thị \({d_2}\) luôn đồng biến.
-
A.
\(m > - 1\,\,;\,\,n < 2\)
-
B.
\(m < - 2\,\,;\,\,n > 1\)
-
C.
\(m < 2\,\,;\,\,\,n > - 1\)
-
D.
\(m > 1\,\,;\,\,\,n < - 2\)
Đáp án: C
Hàm số có phương trình \(y = ax + b\left( {a \ne 0} \right)\): Luôn đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0.\)
Hàm số có đồ thị \({d_1}:y = \left( {m - 2} \right)x + m + 4\) luôn nghịch biến \( \Leftrightarrow m - 2 < 0 \Leftrightarrow m < 2\)
Hàm số có đồ thị \({d_2}:y = \left( {n + 1} \right)x - 3\) luôn đồng biến \( \Leftrightarrow n + 1 > 0 \Rightarrow n > - 1\)
Vậy \(m < 2\) thì hàm số có đồ thị \({d_1}\) luôn nghịch biến.
\(n > - 1\) thì hàm số có đồ thị \({d_2}\) luôn đồng biến.
Tìm các giá trị của \(m\) và của \(n\) để hai đường thẳng \({d_1}\)và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right).\)
-
A.
\(m = - 1;n = 2\)
-
B.
\(m = 1;n = - 2\)
-
C.
\(m = - 1;n = - 2\)
-
D.
\(m = 1;n = 2\)
Đáp án: A
Hai đường thẳng cùng đi qua 1 điểm thì tọa độ của điểm đó đều thỏa mãn hai phương trình đường thẳng.
Hai đường thẳng \({d_1}\) và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right)\) nên ta thay tọa độ điểm A vào hai phương trình ta được:
\(\left\{ \begin{array}{l}0 = \left( {m - 2} \right).1 + m + 4\\0 = \left( {n + 1} \right).1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 2 + m + 4 = 0\\n + 1 - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m = - 2\\n = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 1\\n = 2\end{array} \right.\)
Vậy \(m = - 1;n = 2\).
Cho hai đường thẳng \(\left( d \right):y = \left( {m - 2} \right)x + m\) và \(\left( \Delta \right):y = - 4x + 1\)
Tìm \(m\) để \(\left( d \right)\) song song với \(\left( \Delta \right)\).
-
A.
\(m = 1\)
-
B.
\(m = - 1\)
-
C.
\(m = 2\)
-
D.
\(m = - 2\)
Đáp án: D
Sử dụng điều kiện để hai đường thẳng song song: Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(a = a',\,\,b \ne b'.\)
Để \(\left( d \right)\) song song với \(\left( \Delta \right)\) thì: \(\left\{ \begin{array}{l}m - 2 = - 4\\m \ne 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = - 2\\m \ne 1\end{array} \right. \Rightarrow m = - 2.\)
Vậy \(m = - 2\) thỏa mãn yêu cầu.
Tìm điểm cố định đường thẳng \(\left( d \right)\) luôn đi qua với mọi \(m\).
-
A.
\(A\left( { 1;2} \right)\)
-
B.
\(A\left( { - 1;2} \right)\)
-
C.
\(A\left( { 1;-2} \right)\)
-
D.
\(A\left( { - 1;-2} \right)\)
Đáp án: B
Đưa phương trình về dạng phương trình bậc nhất ẩn \(m\), tìm điều kiện để phương trình có vô số nghiệm, từ đó suy ra tọa độ điểm cố định mà đường thẳng đi qua.
Ta có:
\(\begin{array}{l}y = \left( {m - 2} \right)x + m\\ \Leftrightarrow y = mx - 2x + m\\ \Leftrightarrow \left( {x + 1} \right)m - 2x - y = 0\,\,\,\left( * \right)\end{array}\)
Để phương trình (*) nghiệm đúng với mọi \(m\) thì \(\left\{ \begin{array}{l}x + 1 = 0\\ - 2x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\).
Vậy đường thẳng \(\left( d \right)\) luôn đi qua \(A\left( { - 1;2} \right)\) với mọi \(m\).
Tìm tọa độ điểm \(B\) thuộc \(\left( \Delta \right)\) sao cho \(AB\) vuông góc với \(\left( \Delta \right)\).
-
A.
\(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right).\)
-
B.
\(B\left( {\dfrac{{5}}{{17}};\dfrac{{37}}{{17}}} \right).\)
-
C.
\(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{-37}}{{17}}} \right).\)
-
D.
\(B\left( {\dfrac{{5}}{{17}};\dfrac{{-37}}{{17}}} \right).\)
Đáp án: A
Sử dụng điều kiện để hai đường thẳng vuông góc: Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) vuông góc khi và chỉ khi \(a.a' = - 1\). Tọa độ của giao điểm hai đường thẳng chính là nghiệm của hệ hai phương trình đường thẳng.
Vì đường thẳng \(AB\) đi qua \(A\left( { - 1;2} \right)\) nên gọi phương trình đường thẳng \(AB\)có hệ số góc \(k\):
\(y = k\left( {x + 1} \right) + 2.\)
Mà \(AB \bot \left( \Delta \right) = B\) nên suy ra: \(k.\left( { - 4} \right) = - 1\, \Rightarrow k = \dfrac{1}{4}\)
Khi đó phương trình đường thẳng \(AB\) là: \(y = \dfrac{1}{4}\left( {x + 1} \right) + 2\) hay \(y = \dfrac{1}{4}x + \dfrac{9}{4}.\)
Khi đó tọa độ điểm \(B\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}y = \dfrac{1}{4}x + \dfrac{9}{4}\\y = - 4x + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - \dfrac{5}{{17}}\\y = \dfrac{{37}}{{17}}\end{array} \right. \Rightarrow B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right)\)
Vậy \(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right).\)
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( {{d_m}} \right):y = mx - 2\)\(\left( {m \ne 0} \right)\)
Xác định \(m\) để hàm số \(y = mx - 2\)\(\left( {m \ne 0} \right)\) đồng biến.
-
A.
\(m > 0.\)
-
B.
\(m < 0.\)
-
C.
\(m > 1.\)
-
D.
\(0 < m < 1.\)
Đáp án: A
Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\)đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0\).
Hàm số \(y = mx - 2\) đồng biến\( \Leftrightarrow m > 0\)
Vậy \(m > 0.\)
Chọn A.
Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\)
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m = 3\)
-
D.
\(m = 4\)
Đáp án: D
Một điểm thuộc 1 đường thẳng khi tọa độ điểm đó thỏa mãn phương trình đường thẳng.
Đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\) nên ta thay tọa độ điểm \(A\) vào phương trình đường thẳng \(\left( {{d_m}} \right)\) ta được: \(2 = m.1 - 2 \Rightarrow m = 4\)
Khi \(m = 4\) đường thẳng có phương trình \(y = 4x - 2\)
Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng \(1.\)
-
A.
\(m = 1\) hoặc \(m = - 1\)
-
B.
\(m = 0\)
-
C.
\(m = 1\)
-
D.
\(m = 2\) hoặc \(m = - 2\)
Đáp án: D
Tìm giao điểm của đường thẳng và 2 trục tọa độ, tam giác tạo thành là tam giác vuông.
Điều kiện: \(m \ne 0.\)
+) Với \(y = 0 \Rightarrow mx - 2 = 0 \Rightarrow mx = 2 \Rightarrow x = \dfrac{2}{m}\)
\( \Rightarrow \left( {{d_m}} \right):y = mx - 2\) với cắt \(Ox\) tại điểm \(A\left( {\dfrac{2}{m};\,\,0} \right).\)
+) Với \(x = 0 \Rightarrow y = - 2 \Rightarrow B\left( {0;\,\, - 2} \right)\) là giao của \(\left( {{d_m}} \right)\) và \(Oy.\)
Khi đó diện tích của tam giác sẽ là:
\(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.\left| {\dfrac{2}{m}} \right|.\left| { - 2} \right| = \dfrac{2}{{\left| m \right|}} = 1\\ \Leftrightarrow \left| m \right| = 2 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right..\end{array}\)
Vậy \(m = 2\) hoặc \(m = - 2\) thì đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Trong mặt phẳng tọa độ \(Oxy,\)cho hai đường thẳng \(\left( {{d_1}} \right):y = {m^2}x - {m^4} + 2\) và \(\left( {{d_2}} \right):y = \dfrac{{{m^2}}}{{{m^2} + 1}}x + 2\) (\(m\) là tham số thực khác 0). Tìm tất cả giá trị của tham số \(m\) để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm A duy nhất sao cho diện tích của hình thang \(ABHK\) bằng \(\dfrac{{15}}{2}.\) Biết \(B\left( { - 1;2} \right)\) và hai điểm \(H,K\) lần lượt là hình chiếu vuông góc của \(B\) và A lên trục hoành.
-
A.
\(m = \pm 1\)
-
B.
\(m = \pm 2\)
-
C.
\(m \ne 1\)
-
D.
\(m \ne 2\)
Đáp án : A
Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) theo \(m.\)
Rối sử dụng công thức tính diện tích hình thang để tìm \(m.\)
Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) là:
\(\begin{array}{l}\,\,\,\,\,\,{m^2}x - {m^4} + 2 = \dfrac{{{m^2}}}{{{m^2} + 1}}x + 2\\ \Leftrightarrow {m^2}\left( {{m^2} + 1} \right)x - {m^2}x = {m^4}\left( {{m^2} + 1} \right)\\ \Leftrightarrow {m^2}x = {m^2}\left( {{m^2} + 1} \right)\\ \Leftrightarrow x = {m^2} + 1\,\,\,\,\,\left( {m \ne 0} \right)\\ \Rightarrow y = {m^2} + 2 \Rightarrow A\left( {{m^2} + 1;{m^2} + 2} \right)\end{array}\)
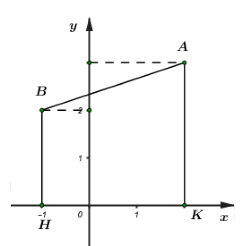
Gọi H, K lần lượt là hình chiếu của B, A lên \(Ox\) nên \(H\left( { - 1;0} \right),K\left( {{m^2} + 1;0} \right)\)
\(\begin{array}{l}{S_{ABHK}} = \dfrac{{15}}{2} \Leftrightarrow \dfrac{{\left( {AK + BH} \right)HK}}{2} = \dfrac{{15}}{2}\\ \Leftrightarrow \left( {AK + BH} \right)HK = 15\\ \Leftrightarrow \left( {{m^2} + 4} \right)\left( {{m^2} + 2} \right) = 15\\ \Leftrightarrow {m^4} + 6{m^2} + 8 = 15\\ \Leftrightarrow {m^4} + 6{m^2} - 7 = 0\\ \Leftrightarrow \left( {{m^2} - 1} \right)\left( {{m^2} + 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} - 1 = 0\\{m^2} + 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} = 1 \Rightarrow m = \pm 1\,\,\,\,\left( {tm} \right)\\{m^2} = - 7\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = \pm 1.\)
Luyện tập và củng cố kiến thức Tổng hợp câu hay và khó chương 2 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Hệ số góc của đường thẳng Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Vị trí tương đối của hai đường thẳng Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Đồ thị hàm số y=ax+b Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Hàm số bậc nhất Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Nhắc lại và bổ sung khái niệm hàm số và đồ thị hàm số Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9