-
Khảo sát chất lượng đầu năm
-
Chương 1 Căn bậc hai - Căn bậc ba
-
Chương 2 Hàm số bậc nhất
-
Chương 3 Hệ hai phương trình bậc nhất hai ẩn
- Bài 1: Phương trình bậc nhất hai ẩn
- Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Bài 3: Giải hệ phương trình bằng phương pháp thế
- Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Hệ phương trình bậc nhất hai ẩn chứa tham số
- Bài 5,6: Giải bài toán bằng cách lập hệ phương trình
- Bài tập hay và khó chương 3 về hệ phương trình
- Bài tập ôn tập chương 3
-
Chương 4 Hàm số y=ax^2. Phương trình bậc hai một ẩn
- Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
- Bài 3,4: Phương trình bậc hai một ẩn và công thức nghiệm
- Bài 5: Công thức nghiệm thu gọn
- Bài 6: Hệ thức Vi-ét và ứng dụng
- Bài 7: Phương trình quy về phương trình bậc hai
- Sự tương giao giữa đường thẳng và Parabol
- Bài 8: Giải bài toán bằng cách lập phương trình
- Hệ phương trình đối xứng
- Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol
- Tổng hợp câu hay và khó về giải bài toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp câu hay và khó về hệ thức Vi-et
- Bài tập ôn tập chương 4
-
Chương 5 Hệ thức lượng trong tam giác vuông
-
Chương 6 Đường tròn
- Sự xác định của đường tròn- Tính chất đối xứng của đường tròn
- Bài 2: Đường kính và dây của đường tròn
- Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn
- Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6: Tính chất hai tiếp tuyến cắt nhau
- Bài 7,8: Vị trí tương đối của hai đường tròn
- Bài tập hay và khó chương đường tròn
- Bài tập ôn tập chương 6
-
Chương 7 Góc với đường tròn
- Bài 1: Góc ở tâm- Số đo cung
- Bài 2: Liên hệ giữa cung và dây
- Bài 3: Góc nội tiếp
- Bài 4: Góc tạo bởi tiếp tuyến và dây cung
- Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn
- Bài 6: Cung chứa góc
- Bài 7: Tứ giác nội tiếp
- Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp
- Bài 9: Độ dài đường tròn, cung tròn
- Bài 10: Diện tích hình tròn, quạt tròn
- Bài tập hay và khó chương góc với đường tròn
- Bài tập vận dụng cao từ các đề thi chuyên
- Bài tập ôn tập chương 7
-
Chương 8 Hình trụ - hình nón - hình cầu
Trắc nghiệm Bài 3: Đồ thị hàm số y=ax+b Toán 9
Đề bài
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
-
A.
Là đường thẳng đi qua gốc tọa độ
-
B.
Là đường thẳng song song với trục hoành
-
C.
Là đường thẳng đi qua hai điểm \(A(0;b),B\left( { - \dfrac{b}{a};0} \right)\) với \(b \ne 0\)
-
D.
Là đường cong đi qua gốc tọa độ
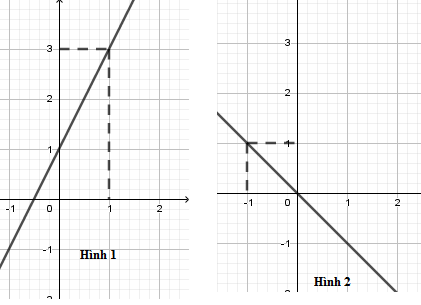
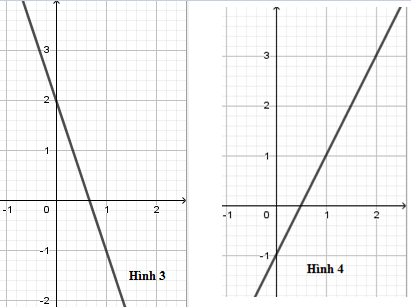
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$
-
A.
Hình 4
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 1
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
-
A.
$A\left( {\dfrac{{ - 5}}{3};0} \right)$
-
B.
$B\left( {1;\dfrac{3}{4}} \right)$
-
C.
$C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$
-
D.
$D\left( {4;\dfrac{4}{3}} \right)$
Cho hai đường thẳng ${d_1}:y = 2x - 2$ và ${d_2}:y = 3 - 4x$. Tung độ giao điểm của ${d_1};{d_2}$ có tọa độ là
-
A.
$y = - \dfrac{1}{3}$
-
B.
$y = \dfrac{2}{3}$
-
C.
$y = 1$
-
D.
$y = - 1$
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
-
A.
$A\left( {\dfrac{1}{6};0} \right)$
-
B.
$B\left( {0;\dfrac{1}{2}} \right)$
-
C.
$C\left( {0;\dfrac{{ - 1}}{6}} \right)$
-
D.
$D\left( {0; - \dfrac{1}{2}} \right)$
Cho hàm số $y = \left( {1 - m} \right)x + m$ . Xác định $m$ để đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$
-
A.
$m = \dfrac{1}{2}$
-
B.
$m = \dfrac{3}{4}$
-
C.
$m = - \dfrac{3}{4}$
-
D.
$m = \dfrac{4}{5}$
Cho hàm số $y = \left( {3 - 2m} \right)x + m - 2$ . Xác định $m$ để đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$.
-
A.
$m = 1$
-
B.
$m = - 1$
-
C.
$m = - 2$
-
D.
$m = 2$
Cho hàm số $y = mx - 2$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = \dfrac{1}{2}x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$.
-
A.
$m = - \dfrac{1}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{1}{2}$
-
D.
$m = - \dfrac{1}{2}$
Cho hàm số $y = \left( {m + 1} \right)x - 1$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = 4$.
-
A.
$m = \dfrac{3}{2}$
-
B.
$m = - \dfrac{3}{2}$
-
C.
$m = \dfrac{2}{3}$
-
D.
$m = - \dfrac{2}{3}$
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Cho ba đường thẳng\({d_1}:y = - 2x;{d_2}:y = - 3x - 1;\)
\({d_3}:y = x + 3.\) Khẳng định nào dưới đây là đúng?
-
A.
Giao điểm của ${d_1}$ và ${d_3}$ là $A\left( {2;1} \right)$.
-
B.
Ba đường thẳng trên không đồng quy
-
C.
Đường thẳng ${d_2}$ đi qua điểm $B\left( {1;4} \right)$
-
D.
Ba đường thẳng trên đồng quy tại điểm $M\left( { - 1;2} \right)$.
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = x;{d_2}:y = 4 - 3x\) và \({d_3}:y = mx - 3\) đồng quy?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = -1$
-
D.
$m = 4$
Cho đường thẳng \(d:y = - 2x - 4\) . Gọi $A,B$ lần lượt là giao điểm của $d$ với trục hoành và trục tung. Tính diện tích tam giác $OAB.$
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$8$
Cho đường thẳng \({d_1}:y = - x + 2\) và ${d_2}:y = 5 - 4x$. Gọi $A,B$ lần lượt là giao điểm của ${d_1}$ với ${d_2}$ và ${d_1}$ với trục hoành. Tổng hoành độ giao điểm của $A$ và $B$ là
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$8$
Gọi \({d_1}\) là đồ thị hàm số \(y = mx + 1\) và \({d_2}\) là đồ thị hàm số \(y = \dfrac{1}{2}x - 2.\)
Xác định giá trị của $m$ để $M\left( {2; - 1} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = - 1$
-
D.
$m = - 2$
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = \left( {m + 2} \right)x - 3;\)
\({d_2}:y = 3x + 1\) và \({d_3}:y = 2x - 5\) giao nhau tại một điểm?
-
A.
$m = \dfrac{1}{3}$
-
B.
$m = - \dfrac{1}{3}$
-
C.
$m = - 1$
-
D.
$m = 1$
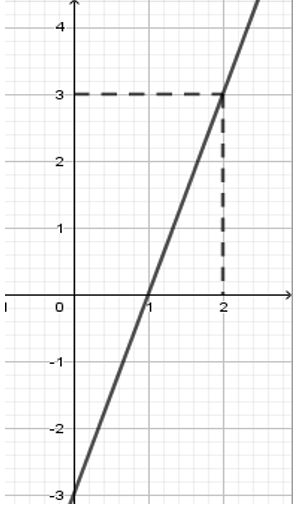
Hình vẽ bên là đồ thị của hàm số nào dưới đây?
-
A.
\(y = 2x - 2\)
-
B.
\(y = 3x - 3\)
-
C.
\(y = x - 1\)
-
D.
\(y = x + 1\)
Lời giải và đáp án
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
-
A.
Là đường thẳng đi qua gốc tọa độ
-
B.
Là đường thẳng song song với trục hoành
-
C.
Là đường thẳng đi qua hai điểm \(A(0;b),B\left( { - \dfrac{b}{a};0} \right)\) với \(b \ne 0\)
-
D.
Là đường cong đi qua gốc tọa độ
Đáp án : C
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng
Trường hợp 1: Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\)
Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$
-
A.
Hình 4
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 1
Đáp án : D
Sử dụng cách vẽ đồ thị hàm số
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng
Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Đồ thị hàm số $y = 2x + 1$ là đường thẳng đi qua hai điểm có tọa độ $\left( {0;1} \right)$ và $\left( {1;3} \right)$ nên hình 1 là đồ thị hàm số $y = 2x + 1$.
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
-
A.
$A\left( {\dfrac{{ - 5}}{3};0} \right)$
-
B.
$B\left( {1;\dfrac{3}{4}} \right)$
-
C.
$C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$
-
D.
$D\left( {4;\dfrac{4}{3}} \right)$
Đáp án : C
Đồ thị hàm số \(y = ax + b(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\)
Thay tọa độ từng điểm vào hàm số ta được
+) Với $A\left( {\dfrac{{ - 5}}{3};0} \right)$. Thay $x = - \dfrac{5}{3};y = 0$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { - \dfrac{5}{3} - 1} \right) + \dfrac{4}{3} = 0 \Leftrightarrow \dfrac{{ - 20}}{3} = 0$ (Vô lý)
+) Với $B\left( {1;\dfrac{3}{4}} \right)$. Thay $x = 1;y = \dfrac{3}{4}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {1 - 1} \right) + \dfrac{4}{3} = \dfrac{3}{4} \Leftrightarrow \dfrac{4}{3} = \dfrac{3}{4}$ (Vô lý)
+) Với $D\left( {4;\dfrac{4}{3}} \right)$. Thay $x = 4;y = \dfrac{4}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {4 - 1} \right) + \dfrac{4}{3} = \dfrac{4}{3} \Leftrightarrow \dfrac{{31}}{3} = \dfrac{4}{3}$ (Vô lý)
+)Với $C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$. Thay $x = \dfrac{2}{3};y = \dfrac{1}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { \dfrac{2}{3} - 1} \right) + \dfrac{4}{3} = \dfrac{1}{3} \Leftrightarrow \dfrac{1}{3} = \dfrac{1}{3}$ (luôn đúng)
$ \Rightarrow C$ thuộc đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$
Cho hai đường thẳng ${d_1}:y = 2x - 2$ và ${d_2}:y = 3 - 4x$. Tung độ giao điểm của ${d_1};{d_2}$ có tọa độ là
-
A.
$y = - \dfrac{1}{3}$
-
B.
$y = \dfrac{2}{3}$
-
C.
$y = 1$
-
D.
$y = - 1$
Đáp án : A
Tìm tọa độ giao điểm của hai đường thẳng theo các bước
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
Xét phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$ ta được
$2x - 2 = 3 - 4x \Leftrightarrow 6x = 5 \Leftrightarrow x = \dfrac{5}{6}$
Thay $x = \dfrac{5}{6}$ vào phương trình đường thẳng ${d_1}:y = 2x - 2$ ta được $y = 2.\dfrac{5}{6} - 2 = - \dfrac{1}{3}$
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
-
A.
$A\left( {\dfrac{1}{6};0} \right)$
-
B.
$B\left( {0;\dfrac{1}{2}} \right)$
-
C.
$C\left( {0;\dfrac{{ - 1}}{6}} \right)$
-
D.
$D\left( {0; - \dfrac{1}{2}} \right)$
Đáp án : D
Tìm tọa độ giao điểm của hai đường thẳng theo các bước
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
Giao điểm của đường thẳng $d$ và trục tung có hoành độ $x = 0$. Thay $x = 0$ vào phương trình $y = 3x - \dfrac{1}{2}$ ta được $y = 3.0 - \dfrac{1}{2} = - \dfrac{1}{2}$.
Vậy tọa độ giao điểm cần tìm là $D\left( {0; - \dfrac{1}{2}} \right)$
Cho hàm số $y = \left( {1 - m} \right)x + m$ . Xác định $m$ để đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$
-
A.
$m = \dfrac{1}{2}$
-
B.
$m = \dfrac{3}{4}$
-
C.
$m = - \dfrac{3}{4}$
-
D.
$m = \dfrac{4}{5}$
Đáp án : B
-Giao điểm của đồ thị hàm số đã cho với trục hoành có tọa độ $M\left( {x;0} \right)$
-Thay tọa độ $M\left( {x;0} \right)$ vào hàm số, giải phương trình thu được để tìm $m$
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$ nên tọa độ giao điểm là $\left( { - 3;0} \right).$
Thay $x = - 3;y = 0$ vào $y = \left( {1 - m} \right)x + m$ ta được $\left( {1 - m} \right).\left( { - 3} \right) + m = 0 $
\( \Leftrightarrow - 3 + 3m + m = 0\)
$\Leftrightarrow 4m - 3 = 0$
$\Leftrightarrow 4m=3$
$ \Leftrightarrow m = \dfrac{3}{4}.$
Vậy $m = \dfrac{3}{4}.$
Cho hàm số $y = \left( {3 - 2m} \right)x + m - 2$ . Xác định $m$ để đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$.
-
A.
$m = 1$
-
B.
$m = - 1$
-
C.
$m = - 2$
-
D.
$m = 2$
Đáp án : C
-Giao điểm của đồ thị hàm số đã cho với trục tung có tọa độ $M\left( {0;y} \right)$
-Thay tọa độ $M\left( {0;y} \right)$vào hàm số, giải phương trình thu được để tìm $m$.
Đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$ nên tọa độ giao điểm là $\left( {0; - 4} \right)$
Thay $x = 0;y = - 4$ vào $y = \left( {3 - 2m} \right)x + m - 2$ ta được $\left( {3 - 2m} \right).0 + m - 2 = - 4 \Leftrightarrow m = - 2$.
Vậy $m = - 2$
Cho hàm số $y = mx - 2$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = \dfrac{1}{2}x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$.
-
A.
$m = - \dfrac{1}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{1}{2}$
-
D.
$m = - \dfrac{1}{2}$
Đáp án : A
Để hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau tại một điểm có hoành độ \(x = {x_0}\).
Bước 1. Viết phương trình hoành độ giao điểm của hai đường thẳng.
Bước 2. Thay \(x = {x_0}\) vào phương trình hoành độ giao điểm để tìm \(m\).
Ta có phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$:
$mx - 2 = \dfrac{1}{2}x + 1$ (*)
Để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$ thì $x = - 4$ thỏa mãn phương trình (*).
Suy ra $m.\left( { - 4} \right) - 2 = \dfrac{1}{2}.\left( { - 4} \right) + 1 $$\Leftrightarrow - 4m - 2 = - 2 + 1 \Leftrightarrow - 4m = 1$
$\Leftrightarrow m = - \dfrac{1}{4}$.
Cho hàm số $y = \left( {m + 1} \right)x - 1$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = 4$.
-
A.
$m = \dfrac{3}{2}$
-
B.
$m = - \dfrac{3}{2}$
-
C.
$m = \dfrac{2}{3}$
-
D.
$m = - \dfrac{2}{3}$
Đáp án : C
Để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = {y_0}$.
Bước 1. Thay $y = {y_0}$ vào phương trình đường thẳng đã biết để tìm ${x_0}$.
Bước 2. Thay $x = {x_0}$; $y = {y_0}$ vào phương trình đường thẳng còn lại để tìm $m$.
Thay $y = 4$ vào phương trình đường thẳng ${d_2}$ ta được $x + 1 = 4 \Leftrightarrow x = 3$.
Suy ra tọa độ giao điểm của ${d_1}$ và ${d_2}$ là $\left( {3;4} \right)$.
Thay $x = 3;y = 4$ vào phương trình đường thẳng ${d_1}$ ta được $\left( {m + 1} \right).3 - 1 = 4 \Leftrightarrow m + 1 = \dfrac{5}{3} \Leftrightarrow m = \dfrac{2}{3}$.
Vậy $m = \dfrac{2}{3}$.
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Đáp án : A
Để hai đường thẳng ${d_1}:y = ax + b$ và ${d_2}:y = a'x + b'$ cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$
Để hai đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung thì
$\left\{ \begin{array}{l} - 2 \ne 5\\m + 2 = 5 - 2m\end{array} \right.$$ \Leftrightarrow 3m = 3 \Leftrightarrow m = 1$.
Cho ba đường thẳng\({d_1}:y = - 2x;{d_2}:y = - 3x - 1;\)
\({d_3}:y = x + 3.\) Khẳng định nào dưới đây là đúng?
-
A.
Giao điểm của ${d_1}$ và ${d_3}$ là $A\left( {2;1} \right)$.
-
B.
Ba đường thẳng trên không đồng quy
-
C.
Đường thẳng ${d_2}$ đi qua điểm $B\left( {1;4} \right)$
-
D.
Ba đường thẳng trên đồng quy tại điểm $M\left( { - 1;2} \right)$.
Đáp án : D
Để xét tính đồng quy của ba đường thẳng cho trước, ta thực hiện các bước sau
Bước 1: Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2: Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thằng còn lại thì kết luận ba đường thẳng đó đồng quy.
+) Thay tọa độ điểm $A\left( {2;1} \right)$ vào phương trình đường thẳng ${d_1}$ ta được $1 = - 2.2 \Leftrightarrow 1 = - 4$ ( vô lý) nên $A \notin {d_1}$ hay $A\left( {2;1} \right)$ không là giao điểm của ${d_1}$ và ${d_3}$. Suy ra A sai.
+) Thay tọa độ điểm $B\left( {1;4} \right)$ vào phương trình đường thẳng ${d_2}$ ta được $4 = - 3.1 - 1 \Leftrightarrow 4 = - 4$ (vô lý )
Nên $B \notin {d_2}$. Suy ra C sai.
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$: $ - 2x = - 3x - 1 \Leftrightarrow x = - 1$$ \Rightarrow y = - 2.\left( { - 1} \right) \Leftrightarrow y = 2$
Suy ra tọa độ giao điểm của ${d_1}$và ${d_2}$ là $\left( { - 1;2} \right)$.
* Thay $x = - 1;y = 2$ vào phương trình đường thẳng ${d_3}$ ta được $2 = - 1 + 3 \Leftrightarrow 2 = 2$ (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm $M\left( { - 1;2} \right)$.
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = x;{d_2}:y = 4 - 3x\) và \({d_3}:y = mx - 3\) đồng quy?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = -1$
-
D.
$m = 4$
Đáp án : D
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2. Thay tọa độ giao điểm vừa tìm được vào đường thẳng còn lại để tìm $m$.
Xét phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$:
$x = 4 - 3x \Leftrightarrow x = 1$$ \Rightarrow y = 1$. Suy ra giao điểm của ${d_1}$ và ${d_2}$ là $M\left( {1;1} \right)$
Để ba đường thẳng trên đồng quy thì $M \in {d_3}$ nên $1 = m.1 - 3 \Leftrightarrow m = 4$.
Vậy $m = 4$.
Cho đường thẳng \(d:y = - 2x - 4\) . Gọi $A,B$ lần lượt là giao điểm của $d$ với trục hoành và trục tung. Tính diện tích tam giác $OAB.$
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$8$
Đáp án : B
Bước 1. Tìm tọa độ giao điểm $A,B$ .
Bước 2. Sử dụng công thức tính diện tích tam giác $OAB$ vuông tại $O$: ${S_{OAB}} = \dfrac{{OA.OB}}{2}$
$A\left( {x;0} \right)$ là giao điểm của $d$ với trục hoành nên $0 = - 2x - 4 \Leftrightarrow x = - 2 \Rightarrow A\left( { - 2;0} \right)$
$B\left( {0;y} \right)$ là giao điểm của $d$ với trục tung nên $y = - 2.0 - 4 \Leftrightarrow y = - 4 \Rightarrow B\left( {0; - 4} \right)$.
Suy ra $OA = \left| { - 2} \right| = 2;OB = \left| { - 4} \right| = 4$.
Vì tam giác $OAB$ vuông tại $O$ nên ${S_{OAB}} = \dfrac{{OA.OB}}{2} = \dfrac{{2.4}}{2} = 4$ (đvdt)
Cho đường thẳng \({d_1}:y = - x + 2\) và ${d_2}:y = 5 - 4x$. Gọi $A,B$ lần lượt là giao điểm của ${d_1}$ với ${d_2}$ và ${d_1}$ với trục hoành. Tổng hoành độ giao điểm của $A$ và $B$ là
-
A.
$2$
-
B.
$4$
-
C.
$3$
-
D.
$8$
Đáp án : C
Tìm tọa độ giao điểm của hai đường thẳng theo các bước
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
+) Phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$ là $ - x + 2 = 5 - 4x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1$ nên ${x_A} = 1$
+) $B\left( {{x_B};0} \right)$ là giao điểm của đường thẳng ${d_1}$ và trục hoành. Khi đó ta có $0 = - {x_B} + 2 \Rightarrow {x_B} = 2$.
Suy ra tổng hoành độ ${x_A} + {x_B} = 1 + 2 = 3$.
Gọi \({d_1}\) là đồ thị hàm số \(y = mx + 1\) và \({d_2}\) là đồ thị hàm số \(y = \dfrac{1}{2}x - 2.\)
Xác định giá trị của $m$ để $M\left( {2; - 1} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = - 1$
-
D.
$m = - 2$
Đáp án : C
Để $M\left( {{x_0};{y_0}} \right)$ là giao của hai đường thẳng ${d_1}$ và ${d_2}$ ta thay tọa độ điểm $M$ vào từng phương trình đường thẳng để tìm $m$.
+) Nhận thấy $M \in {d_2}$.
+) Ta thay tọa độ điểm $M$ vào phương trình ${d_1}$ được phương trình $ - 1 = 2.m + 1 \Leftrightarrow m = - 1$
Vậy $m = - 1$.
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = \left( {m + 2} \right)x - 3;\)
\({d_2}:y = 3x + 1\) và \({d_3}:y = 2x - 5\) giao nhau tại một điểm?
-
A.
$m = \dfrac{1}{3}$
-
B.
$m = - \dfrac{1}{3}$
-
C.
$m = - 1$
-
D.
$m = 1$
Đáp án : A
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2. Thay tọa độ giao điểm vừa tìm được vào đường thẳng còn lại để tìm $m$.
Xét phương trình hoành độ giao điểm của ${d_2}$ và ${d_3}$:
$3x + 1 = 2x - 5 \Leftrightarrow x = - 6$$ \Rightarrow y = - 17$. Suy ra giao điểm của ${d_3}$ và ${d_2}$ là $M\left( { - 6; - 17} \right).$
Để ba đường thẳng trên đồng quy thì $M \in {d_1}$ nên $ - 17 = \left( {m + 2} \right).\left( { - 6} \right) - 3 \Leftrightarrow 6\left( {m + 2} \right) = 14 \Leftrightarrow m = \dfrac{1}{3}$
Vậy $m = \dfrac{1}{3}$.
Hình vẽ bên là đồ thị của hàm số nào dưới đây?
-
A.
\(y = 2x - 2\)
-
B.
\(y = 3x - 3\)
-
C.
\(y = x - 1\)
-
D.
\(y = x + 1\)
Đáp án : B
Sử dụng cách vẽ đồ thị hàm số
Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng
Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ \(\left( {1;0} \right)\) và \(\left( {2;3} \right)\) .
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số \(y = 3x - 3\)
+) Thay \(x = 1;y = 0\) và vào hàm số \(y = 3x - 3\) ta được \(0 = 3 - 3 \Leftrightarrow 0 = 0\) (luôn đúng)
+) Thay \(x = 2;y = 3\) và vào hàm số \(y = 3x - 3\) ta được \(3 = 3.2 - 3 \Leftrightarrow 3 = 3\) (luôn đúng)
Vậy đồ thị hàm số \(y = 3x - 3\) là đường thẳng như hình vẽ.
Luyện tập và củng cố kiến thức Bài 4: Vị trí tương đối của hai đường thẳng Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Hệ số góc của đường thẳng Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp câu hay và khó chương 2 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 2 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Hàm số bậc nhất Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Nhắc lại và bổ sung khái niệm hàm số và đồ thị hàm số Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9
