-
Khảo sát chất lượng đầu năm
-
Chương 1 Căn bậc hai - Căn bậc ba
-
Chương 2 Hàm số bậc nhất
-
Chương 3 Hệ hai phương trình bậc nhất hai ẩn
- Bài 1: Phương trình bậc nhất hai ẩn
- Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Bài 3: Giải hệ phương trình bằng phương pháp thế
- Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Hệ phương trình bậc nhất hai ẩn chứa tham số
- Bài 5,6: Giải bài toán bằng cách lập hệ phương trình
- Bài tập hay và khó chương 3 về hệ phương trình
- Bài tập ôn tập chương 3
-
Chương 4 Hàm số y=ax^2. Phương trình bậc hai một ẩn
- Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
- Bài 3,4: Phương trình bậc hai một ẩn và công thức nghiệm
- Bài 5: Công thức nghiệm thu gọn
- Bài 6: Hệ thức Vi-ét và ứng dụng
- Bài 7: Phương trình quy về phương trình bậc hai
- Sự tương giao giữa đường thẳng và Parabol
- Bài 8: Giải bài toán bằng cách lập phương trình
- Hệ phương trình đối xứng
- Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol
- Tổng hợp câu hay và khó về giải bài toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp câu hay và khó về hệ thức Vi-et
- Bài tập ôn tập chương 4
-
Chương 5 Hệ thức lượng trong tam giác vuông
-
Chương 6 Đường tròn
- Sự xác định của đường tròn- Tính chất đối xứng của đường tròn
- Bài 2: Đường kính và dây của đường tròn
- Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn
- Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6: Tính chất hai tiếp tuyến cắt nhau
- Bài 7,8: Vị trí tương đối của hai đường tròn
- Bài tập hay và khó chương đường tròn
- Bài tập ôn tập chương 6
-
Chương 7 Góc với đường tròn
- Bài 1: Góc ở tâm- Số đo cung
- Bài 2: Liên hệ giữa cung và dây
- Bài 3: Góc nội tiếp
- Bài 4: Góc tạo bởi tiếp tuyến và dây cung
- Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn
- Bài 6: Cung chứa góc
- Bài 7: Tứ giác nội tiếp
- Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp
- Bài 9: Độ dài đường tròn, cung tròn
- Bài 10: Diện tích hình tròn, quạt tròn
- Bài tập hay và khó chương góc với đường tròn
- Bài tập vận dụng cao từ các đề thi chuyên
- Bài tập ôn tập chương 7
-
Chương 8 Hình trụ - hình nón - hình cầu
Trắc nghiệm Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn Toán 9
Đề bài
Cho hình vẽ dưới đây, góc \(BIC\) có số đo bằng
-
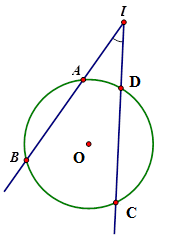
A.
$\dfrac{1}{2}$(sđ \(\overparen{BC} + \) sđ \(\overparen{AD}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{AB} + \) sđ \(\overparen{CD}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{AB} - \) sđ \(\overparen{CD}\) )
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng
-
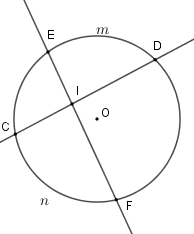
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 70^\circ \) . Tính \(\widehat {ABD}\) .
-
A.
$20^\circ $
-
B.
$15^\circ $
-
C.
$35^\circ $
-
D.
$30^\circ $
Cho \(\left( {O;R} \right)\) và dây \(AB\) bất kỳ. Gọi \(M\) là điểm chính giữa cung nhỏ \(AB\) , \(E;F\) là hai điểm bất kỳ trên dây \(AB\) . Gọi \(C,D\) lần lượt là giao điểm của \(ME;MF\) với \(\left( O \right)\) . Khi đó \(\widehat {EFD} + \widehat {ECD}\) bằng
-
A.
$180^\circ $
-
B.
$150^\circ $
-
C.
$135^\circ $
-
D.
$120^\circ $
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Gọi \(M\) là điểm chính giữa cung \(BC\) . Dây \(AM\) cắt \(OC\) tại \(E\) , dây \(CM\) cắt đường thẳng \(AB\) tại \(N\) .
Tam giác \(MCE\) là tam giác gì?
-
A.
$\Delta MEC$ cân tại \(E\)
-
B.
$\Delta MEC$ cân tại \(M\)
-
C.
$\Delta MEC$ cân tại \(C\)
-
D.
$\Delta MEC$ đều
Hai đoạn thẳng nào sau đây bằng nhau?
-
A.
$BN;BC$
-
B.
\(BN;NC\)
-
C.
\(BC;NC\)
-
D.
$BC;OC$
Tính diện tích tam giác \(CBN\) theo \(R\)
-
A.
\(\dfrac{{{R^2}\sqrt 3 }}{2}\)
-
B.
\(\dfrac{{{R^2}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{R^2}\sqrt 3 }}{2}\)
-
D.
\({R^2}\sqrt 2 \)
Từ \(A\) ở ngoài \(\left( O \right)\) vẽ tiếp tuyến \(AB\) và cát tuyến \(ACD\) . Tia phân giác \(\widehat {BAC}\) cắt \(BC,BD\) lần lượt tại \(M,N\) . Vẽ dây \(BF\) vuông góc với \(MN\) tại \(H\) và cắt \(CD\) tại \(E\) .
Tam giác \(BMN\) là tam giác gì?
-
A.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(N\)
-
B.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(M\)
-
C.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(B\)
-
D.
$\Delta {\rm B}{\rm M}{\rm N}$ đều
Tích $FE.FB$ bằng
-
A.
\(B{E^2}\)
-
B.
\(B{F^2}\)
-
C.
\(D{B^2}\)
-
D.
\(F{D^2}\)
Trên đường tròn \(\left( {O;R} \right)\) vẽ ba dây liên tiếp bằng nhau \(AB = BC = CD\), mỗi dây có độ dài nhỏ hơn \(R\). Các đường thẳng \(AB,CD\) cắt nhau tại \(I\), các tiếp tuyến của \(\left( O \right)\) tại \(B\) và \(D\) cắt nhau tại \(K\) .
Góc $BIC$ bằng góc nào dưới đây?
-
A.
\(\widehat {DKC}\)
-
B.
\(\widehat {DKB}\)
-
C.
\(\widehat {BKC}\)
-
D.
\(\widehat {ICB}\)
$BC$ là tia phân giác của góc nào dưới đây?
-
A.
\(\widehat {KBD}\)
-
B.
\(\widehat {KBO}\)
-
C.
\(\widehat {IBD}\)
-
D.
\(\widehat {IBO}\)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Các tiếp tuyến tại \(B,C\) của \(\left( O \right)\) cắt nhau tại \(M\). Biết \(\widehat {BAC} = 2\widehat {BMC}\). Tính \(\widehat {BAC}\) .
-
A.
\(45^\circ \)
-
B.
\(50^\circ \)
-
C.
\(72^\circ \)
-
D.
\(120^\circ \)
Cho đường tròn \(\left( O \right)\) và một dây \(AB\) . Vẽ đường kính \(CD \bot AB\) (\(D\) thuộc cung nhỏ \(AB\) ). Trên cung nhỏ \(BC\) lấy điểm \(M\) . Các đường thẳng \(CM,DM\) cắt đường thẳng \(AB\) lần lượt tại \(E\) và \(F\) . Tiếp tuyến của đường tròn tại \(M\) cắt đường thẳng \(AB\) tại \(N\). Hai đoạn thẳng nào dưới đây không bằng nhau?
-
A.
\(NM;NE\)
-
B.
\(NM;NF\)
-
C.
\(NE;NF\)
-
D.
\(EN;AE\)
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Trên đường kính \(AB\) lấy điểm \(E\) sao cho \(AE = R\sqrt 2 \). Vẽ dây \(CF\) đi qua \(E\) . Tiếp tuyến của đường tròn tại \(F\) cắt đường thẳng \(CD\) tại \(M\) , dây \(AF\) cắt \(CD\) tại \(N\). Chọn khẳng định sai.
-
A.
\(AC{\rm{//}}MF\)
-
B.
\(\Delta ACE\) cân tại \(A\)
-
C.
\(\Delta ABC\) cân tại \(C\)
-
D.
\(AC{\rm{//}}FD\)
Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Kết luận nào đúng?
-
A.
$\widehat {BID} = \widehat {{\rm{AJ}}E}$
-
B.
$\widehat {BID} = 2\widehat {{\rm{AJ}}E}$
-
C.
$\widehat {2BID} = \widehat {{\rm{AJ}}E}$
-
D.
Các đáp án trên đều sai
Cho đường tròn (O). Từ một điểm M nằm ngoài (O), vẽ các cát tuyến MCA và MBD sao cho góc $\widehat {CMD} = {40^0}$. Gọi E là giao điểm của AD và BC. Biết $\widehat {AEB} = {70^0}$, số đo cung lớn AB là
-
A.
${200^0}$
-
B.
${240^0}$
-
C.
${290^0}$
-
D.
${250^0}$
Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I, K sao cho cung AI = cung AK. Dây IK cắt các cạnh AB, AC lân lượt tại D và E.
-
A.
$\widehat {ADK} = \widehat {ACB}$
-
B.
$\widehat {ADI} = \dfrac{1}{2}\left( {sđ\overparen{AC} + sđ\overparen{CB}} \right)$
-
C.
$\widehat {AEI} = \widehat {ABC}$
-
D.
Tất cả các câu đều đúng
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt các đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt các đường thẳng AB tại I. Chọn đáp án đúng.
-
A.
Các tam giác $FNI,{\rm{ }}INE$ cân
-
B.
$\widehat {IEN} = 2\widehat {NDC}$
-
C.
$\widehat {DNI} = 3\widehat {DCN}$
-
D.
Tất cả các câu đều sai
Lời giải và đáp án
Cho hình vẽ dưới đây, góc \(BIC\) có số đo bằng
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{BC} + \) sđ \(\overparen{AD}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{AB} + \) sđ \(\overparen{CD}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{AB} - \) sđ \(\overparen{CD}\) )
Đáp án : B
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
\(\widehat {BIC} = \)$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Đáp án : A
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
\(\widehat {DIE} = \)$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Đáp án : D
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
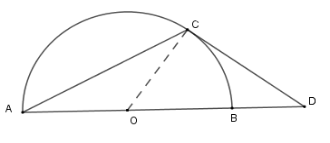
Xét nửa \(\left( O \right)\) có \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BC}\) (góc nội tiếp chắn cung BC) và \(\widehat {CDA} = \dfrac{1}{2}\) (sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\) ) (góc có đỉnh bên ngoài đường tròn)
Mà \(\Delta ADC\) cân tại \(C\) nên \(\widehat {DAC} = \widehat {CDA} \Leftrightarrow \) sđ \(\overparen{BC} = \) sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\)
Suy ra sđ \(\overparen{AC} = 2\). sđ \(\overparen{BC}\)
Mà sđ \(\overparen{AC} + \) sđ \(\overparen{BC} = 180^\circ \) nên sđ \(\overparen{AC} = 120^\circ \) ; sđ\(\overparen{BC}= 60^\circ \)
Do đó $\widehat {ADC} = 30^\circ $.
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 70^\circ \) . Tính \(\widehat {ABD}\) .
-
A.
$20^\circ $
-
B.
$15^\circ $
-
C.
$35^\circ $
-
D.
$30^\circ $
Đáp án : B
Sử dụng góc nội tiếp và góc có đỉnh bên trong đường tròn
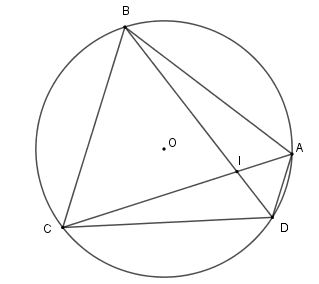
Vì cung \(AB = \) cung \(BC = \) cung \(CD\) nên gọi số đo mỗi cung là $a$ độ. Ta có số đo cung \(AD\) là \(360^\circ - 3a\)
Vì \(\widehat {BIC}\) là góc có đỉnh bên trong đường tròn nên
$\widehat {BIC} = \dfrac{{a + 360^\circ - 3a}}{2} = 70^\circ \Rightarrow a = 110^\circ \Rightarrow $ số đo cung \(AD\) là $360^\circ - 3.110^\circ = 30^\circ $
\(\widehat {ABD}\) là góc nội tiếp chắn cung \(AD\) nên \(\widehat {ABD} = \dfrac{{30^\circ }}{2} = 15^\circ \) .
Cho \(\left( {O;R} \right)\) và dây \(AB\) bất kỳ. Gọi \(M\) là điểm chính giữa cung nhỏ \(AB\) , \(E;F\) là hai điểm bất kỳ trên dây \(AB\) . Gọi \(C,D\) lần lượt là giao điểm của \(ME;MF\) với \(\left( O \right)\) . Khi đó \(\widehat {EFD} + \widehat {ECD}\) bằng
-
A.
$180^\circ $
-
B.
$150^\circ $
-
C.
$135^\circ $
-
D.
$120^\circ $
Đáp án : A
Sử dụng góc nội tiếp và góc có đỉnh bên trong đường tròn.
Ta có \(\widehat {EFD}\) là góc có đỉnh bên trong đường tròn nên
\(\widehat {EFD} = \dfrac{1}{2}\)(sđ \(\overparen{MnA} +\) sđ \(\overparen{BmD}\) )
Và \(\widehat {ECD} = \widehat {MCD} = \dfrac{1}{2}\) sđ \(\overparen{MnD}\)
Từ đó \(\widehat {EFD} + \widehat {ECD} = \dfrac{1}{2}\) (sđ \(\overparen{MnA} + \) sđ \(\overparen{BmD}\)$ + $ sđ \(\overparen{MnD}\))
Mà cung \(AnM = \) cung \(MB\) nên \(\widehat {EFD} + \widehat {ECD} = \dfrac{1}{2}\) (sđ\(\overparen{MB} + \) sđ \(\overparen{BmD}\)$ + $ sđ \(\overparen{MnA} + \)sđ \(\overparen{AD}\) ) =$\dfrac{1}{2}.360^\circ = 180^\circ $.
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Gọi \(M\) là điểm chính giữa cung \(BC\) . Dây \(AM\) cắt \(OC\) tại \(E\) , dây \(CM\) cắt đường thẳng \(AB\) tại \(N\) .
Tam giác \(MCE\) là tam giác gì?
-
A.
$\Delta MEC$ cân tại \(E\)
-
B.
$\Delta MEC$ cân tại \(M\)
-
C.
$\Delta MEC$ cân tại \(C\)
-
D.
$\Delta MEC$ đều
Đáp án: B
Sử dụng góc nội tiếp và góc có đỉnh bên trong đường tròn
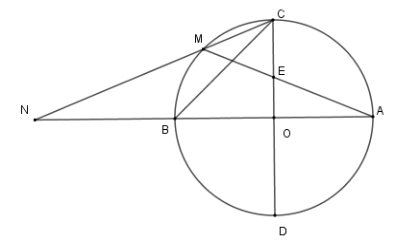
Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên
\(\widehat {MEC} = \dfrac{1}{2}\) (sđ \(\overparen{AD} + \) sđ \(\overparen{MC}\) )
Và \(\widehat {MCE} = \widehat {MCD} \)
\(= \dfrac{1}{2}\) (sđ \(\overparen{BD} + \) sđ \(\overparen{BM}\) )
mà cung \(MB = \) cung \(MC\)
và cung \(AD = \) cung \(BD\)
Từ đó \(\widehat {MEC} = \widehat {MCE} \Rightarrow \Delta MEC\) cân tại \(M\) .
Hai đoạn thẳng nào sau đây bằng nhau?
-
A.
$BN;BC$
-
B.
\(BN;NC\)
-
C.
\(BC;NC\)
-
D.
$BC;OC$
Đáp án: A
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
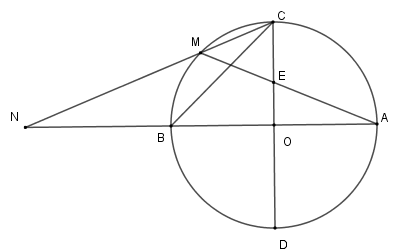
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên
\(\widehat {CNB} = \dfrac{1}{2}\) $ (sđ \overparen{AC}-sđ \overparen{MB})$
Mà sđ $\overparen{MB}$\( = \dfrac{1}{2}\) sđ $\overparen{AC}$ nên \(\widehat {CNA} = \dfrac{1}{2}\)sđ $\overparen{MB}$
Lại có \(\widehat {MCB} = \dfrac{1}{2}\) sđ $\overparen{MB}$ (góc nội tiếp) nên \(\widehat {MCB} = \widehat {BNC} \Rightarrow \Delta BNC\) cân tại \(B \Rightarrow BN = BC\) .
Tính diện tích tam giác \(CBN\) theo \(R\)
-
A.
\(\dfrac{{{R^2}\sqrt 3 }}{2}\)
-
B.
\(\dfrac{{{R^2}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{R^2}\sqrt 3 }}{2}\)
-
D.
\({R^2}\sqrt 2 \)
Đáp án: B
Sử dụng định lý Pytago và công thức diện tích tam giác
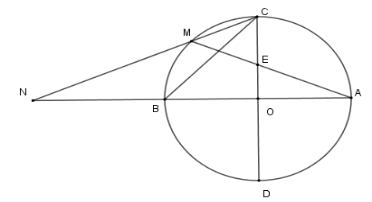
Xét \(\Delta COB\) vuông cân tại \(O\) ta có
\(BC = \sqrt {O{C^2} + O{B^2}} = R\sqrt 2 \)
nên \(BN = R\sqrt 2 \)
Khi đó \({S_{BNC}} = \dfrac{1}{2}NB.CO = \dfrac{{{R^2}\sqrt 2 }}{2}\) .
Từ \(A\) ở ngoài \(\left( O \right)\) vẽ tiếp tuyến \(AB\) và cát tuyến \(ACD\) . Tia phân giác \(\widehat {BAC}\) cắt \(BC,BD\) lần lượt tại \(M,N\) . Vẽ dây \(BF\) vuông góc với \(MN\) tại \(H\) và cắt \(CD\) tại \(E\) .
Tam giác \(BMN\) là tam giác gì?
-
A.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(N\)
-
B.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(M\)
-
C.
$\Delta {\rm B}{\rm M}{\rm N}$ cân tại \(B\)
-
D.
$\Delta {\rm B}{\rm M}{\rm N}$ đều
Đáp án: C
Sử dụng góc có đỉnh bên trong đường tròn và góc có đỉnh bên ngoài đường tròn để chứng minh các góc bằng nhau
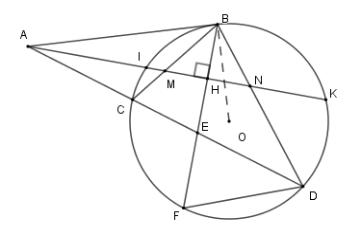
Xét \(\left( O \right)\) có đường thẳng \(AM\) cắt đường tròn tại \(I;K\) .
Khi đó
\(\widehat {BAK} = \dfrac{1}{2}\) (sđ \(\overparen{BK} - \) sđ \(\overparen{BI}\) );
\(\widehat {CAK} = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Mà \(\widehat {BAK} = \widehat {CAK} \)
\(\Rightarrow \) \(\dfrac{1}{2}\) (sđ \(\overparen{BK}- \) sđ \(\overparen{BI}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Nên \( \dfrac{1}{2}\) (sđ \(\overparen{BK} + \) sđ \(\overparen{CI}\) )
\(=\dfrac{1}{2}\) (sđ \(\overparen{DK} + \) sđ \(\overparen{BI}\) )
Hay \(\widehat {BMN} = \widehat {BNM}\)
\(\Rightarrow \Delta BMN\) cân tại \(B\) .
Tích $FE.FB$ bằng
-
A.
\(B{E^2}\)
-
B.
\(B{F^2}\)
-
C.
\(D{B^2}\)
-
D.
\(F{D^2}\)
Đáp án: D
Sử dụng góc nội tiếp để chứng minh các góc bằng nhau để suy ra tam giác đồng dạng từ đó có hệ thức chứng minh.
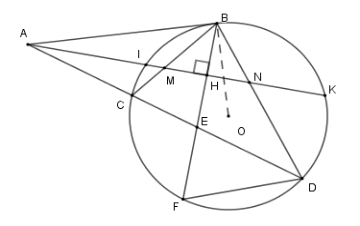
Vì tam giác \(BMN\) cân tại \(B\) có \(BH\) là đường cao nên \(BH\) cũng là đường phân giác.
\( \Rightarrow \widehat {CBF} = \widehat {DBF}\)
\(\Rightarrow \) cung $CF = $ cung \(DF\)
\( \Rightarrow \widehat {DBF} = \widehat {CDF}\) (hệ quả góc nội tiếp)
\( \Rightarrow \Delta FED\backsim\Delta FDB\left( {g - g} \right)\)
\(\Rightarrow \dfrac{{EF}}{{FD}} = \dfrac{{FD}}{{FB}} \Rightarrow FE.FB = F{D^2}\) .
Trên đường tròn \(\left( {O;R} \right)\) vẽ ba dây liên tiếp bằng nhau \(AB = BC = CD\), mỗi dây có độ dài nhỏ hơn \(R\). Các đường thẳng \(AB,CD\) cắt nhau tại \(I\), các tiếp tuyến của \(\left( O \right)\) tại \(B\) và \(D\) cắt nhau tại \(K\) .
Góc $BIC$ bằng góc nào dưới đây?
-
A.
\(\widehat {DKC}\)
-
B.
\(\widehat {DKB}\)
-
C.
\(\widehat {BKC}\)
-
D.
\(\widehat {ICB}\)
Đáp án: B
Sử dụng góc có đỉnh bên ngoài đường tròn để chứng minh các góc bằng nhau
Vì ba dây \(AB = BC = CD \)
\(\Rightarrow \) \(\overparen{AB}= \) \(\overparen{BC} = \) \(\overparen{DC}\)
Xét \(\left( O \right)\) có
\(\widehat {BIC} = \dfrac{1}{2}\) (sđ \(\overparen{AmD}- \) sđ \(\overparen{BC}\) )
\(\widehat {DKB} = \dfrac{1}{2}\) (sđ\(\overparen{BmD} - \) sđ \(\overparen{BnD}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{AmD} + \)sđ\(\overparen{BA} - 2\). sđ\(\overparen{BC}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{AmD} - \) sđ \(\overparen{BC}\) )\( = \widehat {BIC}\)
$BC$ là tia phân giác của góc nào dưới đây?
-
A.
\(\widehat {KBD}\)
-
B.
\(\widehat {KBO}\)
-
C.
\(\widehat {IBD}\)
-
D.
\(\widehat {IBO}\)
Đáp án: A
Sử dụng góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung.
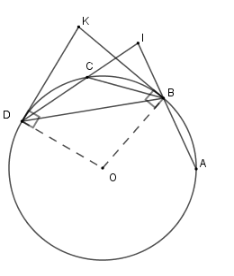
Xét \(\left( O \right)\) có \(\widehat {KBC} = \widehat {CDB}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung)
Lại có \(\widehat {CDB} = \widehat {CBD}\) (hai góc nội tiếp chắn hai cung bằng nhau)
Nên \(\widehat {CBD} = \widehat {KBC} \Rightarrow BC\) là tia phân giác góc \(KBD\) .
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Các tiếp tuyến tại \(B,C\) của \(\left( O \right)\) cắt nhau tại \(M\). Biết \(\widehat {BAC} = 2\widehat {BMC}\). Tính \(\widehat {BAC}\) .
-
A.
\(45^\circ \)
-
B.
\(50^\circ \)
-
C.
\(72^\circ \)
-
D.
\(120^\circ \)
Đáp án : C
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
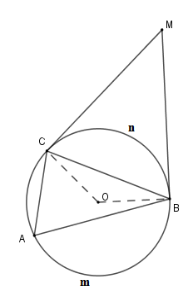
Xét \(\left( O \right)\) có
\(\widehat {BMC} \) \(= \dfrac{1}{2}\) (sđ \(\overparen{BmC} - \) sđ \(\overparen{BnC}\) ) (góc có đỉnh bên ngoài đường tròn)
Và \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BnC}\)
Mà \(\widehat {BAC} = 2\widehat {BMC}\) nên
(sđ \(\overparen{BmC} - \) sđ \(\overparen{BnC}\) )\( = \dfrac{1}{2}\) sđ \( \overparen{BnC}\)
\( \Rightarrow \) sđ \(\overparen{BmC} = \) \(\dfrac{3}{2}\). sđ \(\overparen{BnC}\)
mà sđ \(\overparen{BmC} + \) sđ \(\overparen{BnC}\)$ = 360^\circ $
Nên sđ \(\overparen{BnC}=\) \(\dfrac{{2.360^\circ }}{5} = 144^\circ \) , do đó \(\widehat {BAC} = \dfrac{{120^\circ }}{2} = 72^\circ \) .
Cho đường tròn \(\left( O \right)\) và một dây \(AB\) . Vẽ đường kính \(CD \bot AB\) (\(D\) thuộc cung nhỏ \(AB\) ). Trên cung nhỏ \(BC\) lấy điểm \(M\) . Các đường thẳng \(CM,DM\) cắt đường thẳng \(AB\) lần lượt tại \(E\) và \(F\) . Tiếp tuyến của đường tròn tại \(M\) cắt đường thẳng \(AB\) tại \(N\). Hai đoạn thẳng nào dưới đây không bằng nhau?
-
A.
\(NM;NE\)
-
B.
\(NM;NF\)
-
C.
\(NE;NF\)
-
D.
\(EN;AE\)
Đáp án : D
Sử dụng góc có đỉnh bên ngoài đường tròn, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
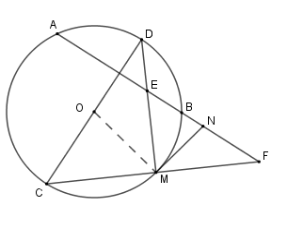
Xét \(\left( O \right)\) có $D$ là điểm chính giữa cung \(AB\) (Vì đường kính \(CD \bot AB\) nên đi qua điểm chính giữa cung \(AB\) )
\(\widehat {NMD} = \dfrac{1}{2}\) sđ \(\overparen{DM}\) (góc tạo bởi tiếp tuyến và dây cung)
\(\widehat {MEN} = \dfrac{1}{2}\) (sđ \(\overparen{MB} + \) sđ \(\overparen{AD}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{MB} + \) sđ \(\overparen{BD}\) )
\( = \widehat {NMD}\)
Suy ra \(\Delta MNE\) cân tại \(N \Rightarrow NE = NM\) (*).
Lại có
\(\widehat {NFM} = \widehat {NMF}\)
(vì \(\widehat {NFM} + \widehat {FEM} = 90^\circ \)
\(= \widehat {NMF} + \widehat {NME}\) và \(\widehat {NME} = \widehat {NEM}\) )
Nên \(\Delta NMF\) cân tại \(N \Rightarrow NF = NM\) (**)
Từ (*) và (**) suy ra \(NE = NF = NM\) .
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Trên đường kính \(AB\) lấy điểm \(E\) sao cho \(AE = R\sqrt 2 \). Vẽ dây \(CF\) đi qua \(E\) . Tiếp tuyến của đường tròn tại \(F\) cắt đường thẳng \(CD\) tại \(M\) , dây \(AF\) cắt \(CD\) tại \(N\). Chọn khẳng định sai.
-
A.
\(AC{\rm{//}}MF\)
-
B.
\(\Delta ACE\) cân tại \(A\)
-
C.
\(\Delta ABC\) cân tại \(C\)
-
D.
\(AC{\rm{//}}FD\)
Đáp án : D
Sử dụng góc có đỉnh bên ngoài đường tròn để chứng minh các góc bằng nhau
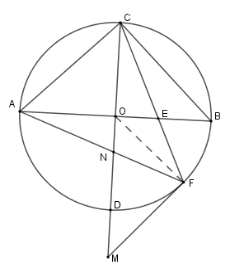
Xét \(\Delta AOC\) vuông cân tại \(O\) có \(AC = \sqrt {O{A^2} + O{C^2}} = R\sqrt 2 \)
\(\Rightarrow AC = AE\) nên \(\Delta AEC\) cân tại \(A \Rightarrow \widehat {ACE} = \widehat {AEC}\)
Hay \(\dfrac{1}{2}\) (sđ \(\overparen{AD} + \) sđ \(\overparen{DF}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{AC}+ \) sđ \(\overparen{BF}\) )
mà \(\overparen{AD} = \) \(\overparen{AC}\) nên \(\overparen{DF}\) \( = \) \(\overparen{BF}\) .
Ta có \(\widehat {ACD} = \dfrac{1}{2}\) sđ \(\overparen{AD}\) ;
\(\widehat {FMC} = \dfrac{1}{2}\) (sđ \(\overparen{FC} - \) sđ \(\overparen{DF}\) )
mà \(\overparen{DF}\) \( = \) \(\overparen{BF}\) .
Nên \(\widehat {FMC} = \dfrac{1}{2}\)sđ \(\overparen{BC}= \dfrac{1}{2}\) sđ \(\overparen{AD}\)\( = \widehat {ACD}\)
Mà hai góc ở vị trí so le trong nên \(AC{\rm{//}}MF\).
Xét tam giác \(CAB\) có \(CO\) là đường trung trực của \(AB\) nên \(\Delta ACB\) cân tại \(C\) .
Phương án A, B, C đúng.
Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Kết luận nào đúng?
-
A.
$\widehat {BID} = \widehat {{\rm{AJ}}E}$
-
B.
$\widehat {BID} = 2\widehat {{\rm{AJ}}E}$
-
C.
$\widehat {2BID} = \widehat {{\rm{AJ}}E}$
-
D.
Các đáp án trên đều sai
Đáp án : A
+) Nhận biết được góc có đỉnh nằm ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn
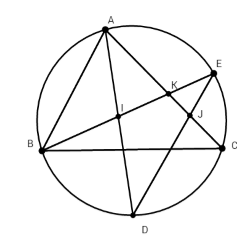
Ta có $\widehat {BID}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung BD và AE
$ \Rightarrow \widehat {BID} = \dfrac{1}{2}\left( {s{\rm{đ}}\overparen{BD} + sđ\overparen{AE}} \right)$
+) $\widehat {{\rm{AJ}}E}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung CD và AE
\( \Rightarrow \widehat {AJE} = \dfrac{1}{2}(sđ\overparen{AE }+ \)sđ\(\overparen{DC})\)
Mà AD là phân giác của góc A nên sđ$\overparen{BD} = $sđ$\overparen{CD}$
Suy ra $\widehat {BID} = \widehat {{\rm{AJ}}E}$
Cho đường tròn (O). Từ một điểm M nằm ngoài (O), vẽ các cát tuyến MCA và MBD sao cho góc $\widehat {CMD} = {40^0}$. Gọi E là giao điểm của AD và BC. Biết $\widehat {AEB} = {70^0}$, số đo cung lớn AB là
-
A.
${200^0}$
-
B.
${240^0}$
-
C.
${290^0}$
-
D.
${250^0}$
Đáp án : C
+) Nhận biết được góc có đỉnh nằm ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn
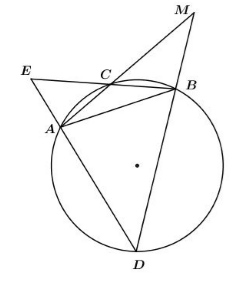
$\begin{array}{l}\widehat {DEB} = \dfrac{1}{2}\left( {sđ\overparen{DB} - sđ\overparen{AC}} \right) = {70^0}\\ \Rightarrow s{\rm{đ}}\overparen{DB} - sđ\overparen{AC} = {140^0}\left( 1 \right)\\\widehat {AMD} = \dfrac{1}{2}\left( {sđ\overparen{AD} - sđ\overparen{BC}} \right) = {40^0}\\ \Rightarrow sđ\overparen{AD} - sđ\overparen{BC} = {80^0}\left( 2 \right)\\sđ\overparen{AC} + sđ\overparen{CB} + sđ\overparen{DB} + sđ\overparen{AD} = {360^0}\left( 3 \right)\\(1) + (2) + (3) \Rightarrow 2\left( {sđ\overparen{DB} + sđ\overparen{AD}} \right) = {580^0}\\ \Leftrightarrow sđ\overparen{DB} + sđ\overparen{AD} = {290^0}\\ \Leftrightarrow sđ\overparen{AB} = {290^0}\end{array}$
Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I, K sao cho cung AI = cung AK. Dây IK cắt các cạnh AB, AC lân lượt tại D và E.
-
A.
$\widehat {ADK} = \widehat {ACB}$
-
B.
$\widehat {ADI} = \dfrac{1}{2}\left( {sđ\overparen{AC} + sđ\overparen{CB}} \right)$
-
C.
$\widehat {AEI} = \widehat {ABC}$
-
D.
Tất cả các câu đều đúng
Đáp án : D
+) Nhận biết được góc có đỉnh nằm trong đường tròn, góc nội tiếp
+) Tính được số đo góc nằm trong đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn, mối uan hệ giữa số đo cung và dây cung
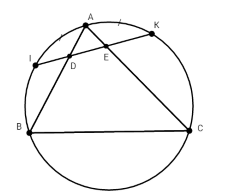
+) Ta có $\widehat {ADK}$ là góc có đỉnh nằm trong đường tròn nên
$\begin{array}{l}\widehat {ADK} = \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{IB}} \right) = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{IB}} \right)\\ = \dfrac{1}{2}sđ\overparen{AB} = \widehat {ACB}\end{array}$
+)Ta có $\widehat {ADI}$ là góc có đỉnh nằm trong đường tròn nên
$\begin{array}{l}\widehat {ADI} = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{AK}} \right) \\= \dfrac{1}{2}sđ\overparen{AB} = \dfrac{1}{2}\left( {sđ\overparen{AC} + sđ\overparen{CB}} \right)\end{array}$
+)Ta có $\widehat {AEI}$ là góc có đỉnh ở trong đường tròn nên
$\widehat {AEI} = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{KC}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{KC}} \right) = \dfrac{1}{2}sđ\overparen{AC} = \widehat {ABC}$
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt các đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt các đường thẳng AB tại I. Chọn đáp án đúng.
-
A.
Các tam giác $FNI,{\rm{ }}INE$ cân
-
B.
$\widehat {IEN} = 2\widehat {NDC}$
-
C.
$\widehat {DNI} = 3\widehat {DCN}$
-
D.
Tất cả các câu đều sai
Đáp án : A
+) Nhận biết được góc có đỉnh nằm trong, ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm trong, ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn, mối uan hệ giữa số đo cung và dây cung
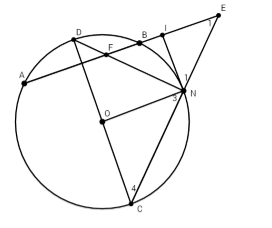
Ta có tam giác AOB cân tại O nên dễ dàng chỉ ra được $sđ\overparen{AD} = sđ\overparen{DB}$
$\begin{array}{l}\widehat {IFN} = \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{AD}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{BD}} \right)\\ = \dfrac{1}{2}sđ\overparen{DN} = \widehat {INF}\end{array}$
Suy ra tam giác FIN cân tại I
Ta có:
$\begin{array}{l}{\widehat N_1} + \widehat {{N_3}} = {90^0} \Rightarrow {\widehat N_1} + \widehat {{C_4}} = {90^0}\\\widehat {{E_1}} = \dfrac{1}{2}\left( {sđ\overparen{AC} - sđ\overparen{BN}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{BC} - sđ\overparen{CN}} \right) = \dfrac{1}{2}sđ\overparen{NC}\\ \Rightarrow \widehat {{C_4}} + \widehat {{E_1}} = \dfrac{1}{2}sđ\overparen{DN} + \dfrac{1}{2}sđ\overparen{NC} \\= \dfrac{1}{2}sđ\overparen{DC} = {90^0}\\ \Rightarrow \widehat {{E_1}} = \widehat {{N_1}}\end{array}$
Do đó \(\Delta INE\) cân tại I.
Luyện tập và củng cố kiến thức Bài 6: Cung chứa góc Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Tứ giác nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Độ dài đường tròn, cung tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Diện tích hình tròn, quạt tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập hay và khó chương góc với đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập vận dụng cao từ các đề thi chuyên Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 7 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Góc tạo bởi tiếp tuyến và dây cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Góc nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Liên hệ giữa cung và dây Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Góc ở tâm- Số đo cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9
