-
CHƯƠNG 1. SỐ HỮU TỈ - SỐ THỰC
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC – ĐƯỜNG THẲNG SONG SONG
-
CHƯƠNG 2. TAM GIÁC
-
Chủ đề 3: Tam giác - Tam giác bằng nhau
- 1. Tổng ba góc trong một tam giác
- 2. Hai tam giác bằng nhau
- 3. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh - cạnh - cạnh (c.c.c)
- 4. Trường hợp bằng nhau thứ hai của tam giác: Cạnh - góc - cạnh (c.g.c)
- 5. Trường hợp bằng nhau thứ ba của tam giác: Góc - góc - góc (g.g.g)
- Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
- Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
-
Chủ đề 4. Tam giác cân - Định lý Pythagore
-
Ôn tập chương 2 - Hình học 7
-
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4. BIỂU THỨC ĐẠI SỐ
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC – CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
-
Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- 1. Quan hệ giữa góc và cạnh trong một tam giác
- 2. Quan hệ giữa đường vuông góc và đường xiên – Giữa đường xiên và hình chiếu
- 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
-
Chủ đề 6 : Các đường đồng quy của tam giác
- 1. Tính chất ba đường trung tuyến của tam giác
- 2. Tính chất tia phân giác của một góc
- 3. Tính chất ba đường phân giác của tam giác
- 4. Tính chất đường trung trực của một đoạn thẳng
- 5. Tính chất ba đường trung trực của tam giác
- 6. Tính chất ba đường cao trong tam giác
- Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
- Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác
-
Ôn tập chương 3 – Hình học
-
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Bài tập - Chủ đề 1: Góc tạo bởi các đường thẳng
Bài tập 13 trang 116 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho hình 17.
Đề bài
Cho hình 17.
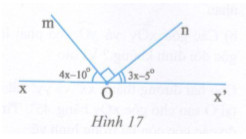
a) Tính số đo \(\widehat {xOm}\) và \(\widehat {x'On}\)
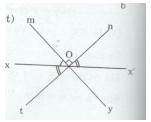
b) Vẽ tia Ot sao cho \(\widehat {xOt}\) và \(\widehat {nOx'}\) là hai góc đối đỉnh. Trên nửa mặt phẳng bờ xx’ chứa tia Ot, vẽ tia Oy sao cho \(\widehat {tOy} = {90^o}\). Hai góc mOn và tOy có là hai góc đối đỉnh không ? Vì sao ?
Lời giải chi tiết
a)Ta có: \(\widehat {xOm} + \widehat {mOn} + \widehat {n0x'} = {180^0}\) (vì góc xOx’ là góc bẹt)
Nên \(4x - {10^0} + {90^0} + 3x - {5^0} = {180^0}.\)
Do đó: \(\eqalign{ & 7x = {180^0} - {90^0} + {10^0} + {5^0} = {105^0}. \cr & \Rightarrow x = {105^0}:7 = {15^0} \cr} \)
Vậy \(\widehat {xOm} = 4x - {10^0} = 4.15 - {10^0} = {50^0}.\)
Và \(\widehat {x'On} = 3x - {5^0} = 3.15 - {5^0} = {40^0}.\)
b) Ta có: góc xOt và nOx’ là hai góc đối đỉnh
=> On và Ot là hai tia đối nhau \( \Rightarrow \widehat {nOt} = {180^0}.\)
Do đó:
\(\eqalign{ & \widehat {n0x'} + \widehat {y0x'} + \widehat {yOt} = {180^0} \cr & \Rightarrow {40^0} + \widehat {y0x'} + {90^0} = {180^0} \Rightarrow \widehat {y0x'} = {180^0} - {90^0} - {40^0} = {50^0} \cr} \)
Ta có: \(\widehat {mOn} + \widehat {n0x'} + \widehat {y0x'} = {90^0} + {40^0} + {50^0} = {180^0}\)
\( \Rightarrow \widehat {mOy} = {180^0} \Rightarrow \) Om và Oy là hai tia đối nhau.
Vậy góc mOn và yOt là hai góc đối đỉnh.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 14 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 15 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 16 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 17 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 18 trang 116 Tài liệu dạy – học Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
Danh sách bình luận